
Moody diagramligninger, hvad det er til, applikationer
Det lunefuldt diagram består af en række kurver tegnet på logaritmisk papir, som bruges til at beregne friktionsfaktoren til stede i strømmen af en turbulent væske gennem en cirkulær kanal.
Med friktionsfaktor F friktionsenergitab evalueres, en vigtig værdi for at bestemme den korrekte ydeevne for pumper, der distribuerer væsker såsom vand, benzin, råolie og andre.

For at kende energien i strømmen af en væske er det nødvendigt at kende gevinster og tab på grund af faktorer som hastighed, højde, tilstedeværelsen af enheder (pumper og motorer), virkningerne af væskens viskositet og friktion mellem den. rørets vægge.
Artikelindeks
- 1 Ligninger for energien i en væske i bevægelse
- 1.1 -Friktionsfaktor og Reynolds-nummer
- 2 Hvad er det til??
- 3 Hvordan fremstilles det, og hvordan bruges det??
- 3.1 - Arbejdet eksempel 1
- 4 applikationer
- 4.1 -Løst eksempel 2
- 5 Referencer
Ligninger for energien i en flydende væske
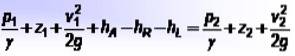
- s1 Y sto er trykket på hvert punkt,
- z1 Y zto er højderne i forhold til referencepunktet,
- v1 Y vto er de respektive væskehastigheder,
- hTIL er den energi, der tilføjes af pumper, hR er den energi, der tages af en eller anden enhed, såsom en motor, og hL dækker væskeenergitab på grund af friktion mellem væske- og rørvæggene samt andre mindre tab.
Værdien af hL beregnes ved hjælp af Darcy-Weisbach-ligningen:
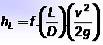
Hvor L er rørets længde, D er dens indvendige diameter, v er væskens hastighed og g er værdien af accelerationen på grund af tyngdekraften. Dimensionerne af hL er længde, og normalt er enhederne, hvori det er repræsenteret, meter eller fødder.
-Friktionsfaktor og Reynolds nummer
At beregne F empiriske ligninger opnået fra eksperimentelle data kan anvendes. Det er nødvendigt at skelne mellem, om det er en væske i et laminært regime eller i et turbulent regime. Til det laminære regime F let vurderet:
f = 64 / NR
Hvor NR er Reynolds-nummeret, hvis værdi afhænger af det regime, hvor væsken er. Kriterierne er:
Laminær strømning: NR < 2000 el flujo es laminar; Flujo turbulento NR > 4000; Overgangsordning: 2000 < NR < 4000
Reynolds-nummeret (dimensionsløst) afhænger igen af væskens hastighed v, rørets indvendige diameter D og den kinematiske viskositet n af væsken, hvis værdi opnås ved hjælp af tabeller:
NR = v.D / n
Colebrook ligning
For en turbulent strømning er den mest accepterede ligning i kobber- og glasrør Cyril Colebrook (1910-1997), men den har den ulempe, at F det er ikke eksplicit:
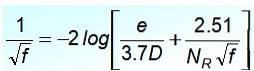
I denne ligning kvotienten e / D er den relative ruhed af røret og NR er Reynolds-nummeret. En omhyggelig observation viser, at det ikke er let at lade F til venstre for ligestillingen, så det er ikke egnet til øjeblikkelige beregninger.
Colebrook selv foreslog denne tilgang, som er eksplicit, gyldig med nogle begrænsninger:

Hvad er det for?
Moody-diagrammet er nyttigt til at finde friktionsfaktoren F inkluderet i Darcys ligning, da det i Colebrooks ligning ikke er let at udtrykke F direkte med hensyn til andre værdier.
Dens anvendelse forenkler opnåelse af værdien af F, ved at indeholde den grafiske gengivelse af F i funktion af NR for forskellige værdier af relativ ruhed på en logaritmisk skala.
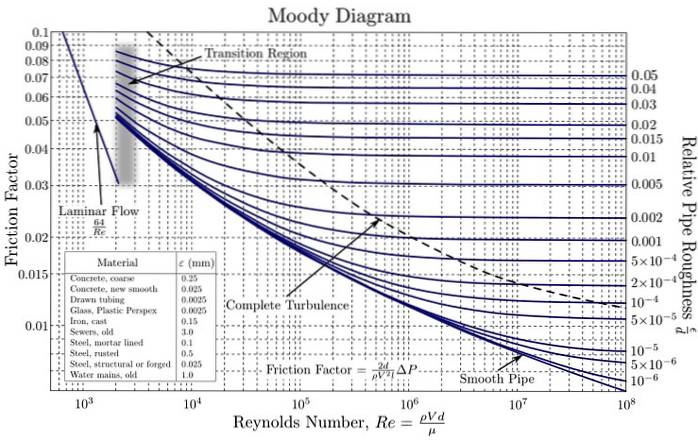
Disse kurver er oprettet ud fra eksperimentelle data med forskellige materialer, der almindeligvis anvendes i rørfremstilling. Brug af en logaritmisk skala for begge F som for NR det er nødvendigt, da de dækker en meget bred vifte af værdier. På denne måde letter grafikken af værdier af forskellige størrelsesordener..
Den første graf over Colebrook-ligningen blev opnået af ingeniøren Hunter Rouse (1906-1996) og kort efter blev den modificeret af Lewis F. Moody (1880-1953) i den form, som den bruges i dag..
Det bruges til både cirkulære og ikke-cirkulære rør, simpelthen erstatte den hydrauliske diameter for disse.
Hvordan fremstilles det, og hvordan bruges det??
Som forklaret ovenfor er Moody-diagrammet lavet af adskillige eksperimentelle data præsenteret i grafisk form. Her er trinene til at bruge det:
- Beregn Reynolds nummer NR for at bestemme, om strømningen er laminær eller turbulent.
- Beregn den relative ruhed ved hjælp af ligningen ogr = e / D., hvor og er materialets absolutte ruhed, og D er rørets indvendige diameter. Disse værdier opnås gennem tabeller.
- Nu hvor du har det ogr Y NR, projekt lodret, indtil kurven svarer til ogr opnået.
- Projekter vandret og til venstre for at læse værdien af F.
Et eksempel hjælper med at let visualisere, hvordan diagrammet bruges.
-Arbejdet eksempel 1
Bestem friktionsfaktoren for vand ved 160 ° F, der flyder med en hastighed på 22 ft / s i en kanal lavet af ubestrøget smedejern med en indvendig diameter på 1 in..
Opløsning
Nødvendige data (findes i tabeller):
Kinematisk viskositet af vand ved 160ºF: 4,38 x 10-6 fodto/ s
Absolut ruhed af ubestrøget smedejern: 1,5 x 10 -4 fødder
Første skridt
Reynolds-tallet beregnes, men ikke før den indre diameter overføres fra 1 tomme til fødder:
1 tomme = 0,0833 fod
NR = (22 x 0,0833) / 4,38 x 10-6= 4,18 x 10 5
I henhold til de tidligere viste kriterier er det en turbulent strømning, så giver Moody-diagrammet mulighed for at opnå den tilsvarende friktionsfaktor uden at skulle bruge Colebrook-ligningen.
Andet trin
Du skal finde den relative ruhed:
ogr = 1,5 x 10-4 / 0,0833 = 0,0018
Tredje trin
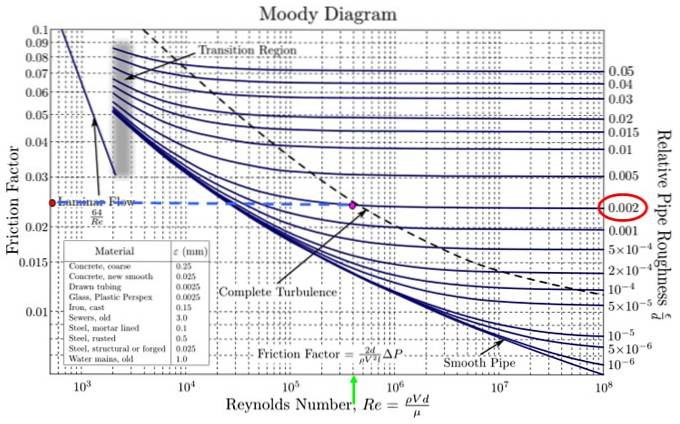
I det medfølgende Moody-diagram er det nødvendigt at gå yderst til højre og finde den nærmeste relative ruhed til den opnåede værdi. Der er ingen, der svarer nøjagtigt til 0,0018, men der er en, der er ret tæt, den på 0,002 (rød oval i figuren).
Samtidig søges det tilsvarende Reynolds-nummer på den vandrette akse. Den nærmeste værdi til 4,18 x 10 5 er 4 x 10 5 (grøn pil i figuren). Skæringspunktet mellem begge er fuchsia-punktet.
Fjerde trin
Projicer til venstre efter den blå stiplede linje, og nå det orange punkt. Anslå nu værdien af F, under hensyntagen til, at divisionerne ikke er af samme størrelse, da de er en logaritmisk skala på både den vandrette og lodrette akse.
Moody-diagrammet i figuren har ikke fine vandrette opdelinger, derfor er værdien af F i 0,024 (det er mellem 0,02 og 0,03, men det er ikke halvt, men lidt mindre).
Der er lommeregnere online, der bruger Colebrook ligningen. En af dem (se referencer) leverede værdien 0,023664639 for friktionsfaktoren.
Ansøgninger
Moody-diagrammet kan anvendes til at løse tre typer problemer, forudsat at væsken og rørets absolutte ruhed er kendt:
- Beregning af trykfaldet eller trykforskellen mellem to punkter forudsat rørets længde, højdeforskellen mellem de to punkter, der skal tages i betragtning, hastigheden og rørets indvendige diameter.
- Bestemmelse af strømningen, idet man kender rørets længde og diameter plus det specifikke trykfald.
- Evaluering af rørets diameter, når længde, flow og trykfald mellem de punkter, der skal overvejes, er kendt.
Problemer af den første type løses direkte ved hjælp af diagrammet, mens de af den anden og tredje type kræver brug af en computerpakke. For eksempel i den tredje type, hvis rørets diameter ikke er kendt, kan Reynolds-antallet ikke vurderes direkte eller den relative ruhed..
En måde at løse dem på er at antage en indledende indre diameter og derfra successivt justere værdierne for at opnå det trykfald, der er specificeret i problemet..
-Arbejdet eksempel 2
Du har 160 ° F vand, der strømmer støt langs et ubelagt smedejernrør med en diameter på 1 tommer med en hastighed på 22 ft / s. Bestem trykforskellen forårsaget af friktion og den pumpekraft, der kræves for at opretholde strømning i en længde af vandret rør L = 200 fod langt..
Opløsning
Nødvendige data: tyngdeacceleration er 32 ft / sto ; vandets specifikke tyngdekraft ved 160 ºF er γ = 61,0 lb-kraft / ft3
Dette er røret fra løst eksempel 1, derfor er friktionsfaktoren allerede kendt F, som er estimeret til 0,0024. Denne værdi tages med i Darcy-ligningen for at evaluere friktionstab:

Den krævede pumpeeffekt er:
W = v. A. (s1 - sto)
Hvor A er rørets tværsnitsareal: A = p. (Dto/ 4) = s. (0,0833to/ 4) fodto = 0,00545 fodto
W = 22 ft / s. 2659,6 lb-kraft / ftto. 0,00545 fodto= 318,9 lb-kraft. fødder
Effekt udtrykkes bedst i watt, som konverteringsfaktoren kræves for:
1 Watt = 0.737 lb-kraft. fødder
Derfor er den krævede effekt for at opretholde strømmen W = 432,7 W.
Referencer
- Cimbala, C. 2006. Fluid Mechanics, Fundamentals and Applications. Mc. Graw Hill. 335-342.
- Franzini, J. 1999. Fluid Mechanics with Application is in Engineering. Mc. Graw Hill. 176-177.
- LMNO Engineering. Moody Friction Factor Calculator. Gendannet fra: lmnoeng.com.
- Mott, R. 2006. Fluid Mechanics. 4. plads Udgave. Pearson Uddannelse. 240-242.
- Ingeniørværktøjskassen. Humørdiagram. Gendannet fra: engineeringtoolbox.com
- Wikipedia. Moody Chart. Gendannet fra: en.wikipedia.org


Endnu ingen kommentarer