
Lineær dilatation hvad er det, formel og koefficienter, eksempel
Det lineær udvidelse opstår, når et objekt oplever ekspansion på grund af en variation i temperaturen, overvejende i en dimension. Dette skyldes materialets egenskaber eller dets geometriske form..
For eksempel i en ledning eller en stang, når der er en stigning i temperaturen, er det længden, der lider under den største ændring på grund af termisk ekspansion..

Kablerne, hvorpå fuglene i den foregående figur sidder, strækker sig, når deres temperatur stiger; i stedet trækker de sig sammen, når de køler af. Det samme sker for eksempel med stængerne, der danner skinnerne på en jernbane.
Artikelindeks
- 1 Hvad er lineær udvidelse??
- 2 Formel for lineær udvidelse og dens koefficient
- 2.1 Koefficient for lineær ekspansion for forskellige materialer
- 3 Arbejdede eksempler på lineær ekspansion
- 3.1 Eksempel 1
- 3.2 Eksempel 2
- 3.3 Eksempel 3
- 3.4 Eksempel 4
- 4 Referencer
Hvad er lineær udvidelse?
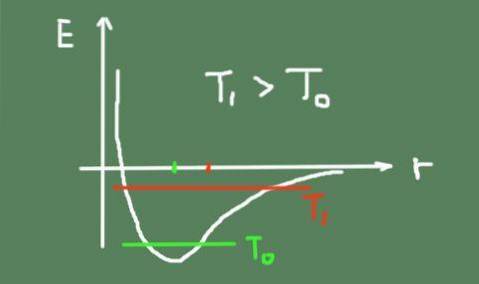
I et fast materiale opretholder atomerne deres relative positioner mere eller mindre faste omkring et ligevægtspunkt. På grund af termisk omrøring svinger de imidlertid altid omkring det samme.
Når temperaturen stiger, øges den termiske svingning også, hvilket får de midterste svingningspositioner til at ændre sig. Dette skyldes, at bindingspotentialet ikke ligefrem er parabolsk og har asymmetri omkring minimumet.
Nedenfor er en figur, der skitserer den kemiske bindingsenergi som en funktion af den interatomiske afstand. Det viser også den samlede svingningsenergi ved to temperaturer, og hvordan svingningens centrum bevæger sig.
Formel for lineær udvidelse og dens koefficient
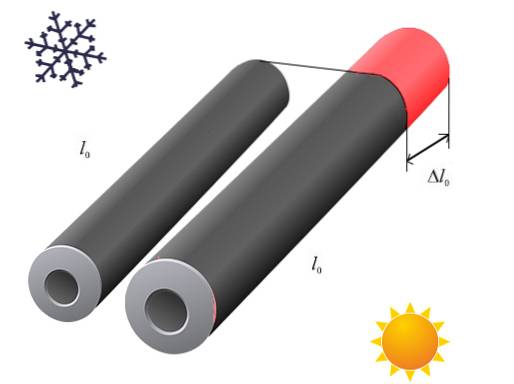
For at måle lineær ekspansion starter vi med en indledende længde L og en indledende temperatur T af det objekt, hvis ekspansion skal måles..
Antag at dette objekt er en stang, hvis længde er L, og tværsnitsdimensionerne er meget mindre end L.
Dette objekt udsættes først for en temperaturvariation AT, således at den endelige temperatur for objektet, når den termiske ligevægt med varmekilden er etableret, vil være T '= T + AT.
Under denne proces vil længden af objektet også have ændret sig til en ny værdi L '= L + ΔL, hvor ΔL er variationen i længden.
Koefficienten for lineær ekspansion α defineres som kvotienten mellem den relative variation i længde pr. Enhedsvariation i temperatur. Den følgende formel definerer koefficienten for lineær ekspansion a:
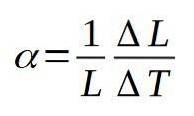
Dimensionerne for koefficienten for lineær ekspansion er dimensioner for den inverse temperatur.
Koefficient for lineær ekspansion for forskellige materialer
Dernæst vil vi give en liste over koefficienten for lineær ekspansion for nogle typiske materialer og elementer. Koefficienten beregnes ved normalt atmosfærisk tryk baseret på en omgivelsestemperatur på 25 ° C; og dens værdi betragtes som konstant i et AT-interval på op til 100 ° C.
Enheden for koefficienten for lineær ekspansion vil være (° C)-1.
- Stål: α = 12 ∙ 10-6 (° C)-1
- Aluminium: α = 23 ∙ 10-6 (° C)-1
- Guld: α = 14 ∙ 10-6 (° C)-1
- Kobber: α = 17 ∙ 10-6 (° C)-1
- Messing: α = 18 ∙ 10-6 (° C)-1
- Jern: α = 12 ∙ 10-6 (° C)-1
- Glas: α = (7 til 9) ∙ 10-6 (° C)-1
- Kviksølv: α = 60,4 ∙ 10-6 (° C)-1
- Kvarts: α = 0,4 ∙ 10-6 (° C)-1
- Diamant: α = 1,2 ∙ 10-6 (° C)-1
- Bly: α = 30 ∙ 10-6 (° C)-1
- Egtræ: α = 54 ∙ 10-6 (° C)-1
- PVC: α = 52 ∙ 10-6 (° C)-1
- Kulfiber: α = -0,8 ∙ 10-6 (° C)-1
- Beton: α = (8 til 12) ∙ 10-6 (° C)-1
De fleste materialer strækker sig med en stigning i temperaturen. Imidlertid krymper nogle specielle materialer såsom kulfiber med stigende temperatur..
Arbejdede eksempler på lineær udvidelse
Eksempel 1
Et kobberkabel hænges mellem to poler, og dets længde på en kølig dag ved 20 ° C er 12 m. Beregn værdien af dens længde på en varm dag ved 35 ° C.
Opløsning
Startende med definitionen af koefficienten for lineær ekspansion og at vide, at for kobber er denne koefficient lig med: α = 17 ∙ 10-6 (° C)-1
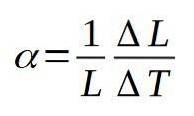
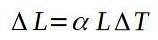
Kobberkablet gennemgår en stigning i længden, men det er kun 3 mm. Kablet går fra at have 12.000 m til at have 12.003 m.
Eksempel 2
I en smedje går en aluminiumsstang ud af ovnen ved 800 grader Celsius og måler en længde på 10,00 m. Når det er afkølet til stuetemperatur på 18 grader Celsius, skal du bestemme, hvor lang søjlen vil være.
Opløsning
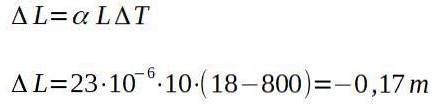
Med andre ord vil bjælken, når den er kold, have en samlet længde på:
9,83 m.
Eksempel 3
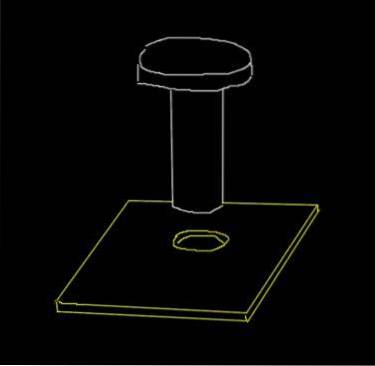
En stålnitte har en diameter på 0,915 cm. På en aluminiumsplade er der lavet et hul på 0,910 cm. Dette er de indledende diametre, når den omgivende temperatur er 18 ° C.
Til hvilken minimumstemperatur skal pladen opvarmes, for at nitten kan passere gennem hullet? Formålet med dette er, at når nitten vender tilbage til stuetemperatur, vil nitten sidde tæt på pladen.
Opløsning
Selvom pladen er en overflade, er vi interesserede i udvidelsen af hullets diameter, som er en endimensionel størrelse..
Lad os kalde D0 til den originale diameter af aluminiumspladen og D, som den en gang er opvarmet til.
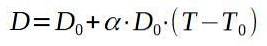
Løsning for den endelige temperatur T har vi:
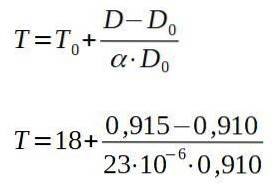
Resultatet af de tidligere operationer er 257 ° C, hvilket er den mindste temperatur, som pladen skal opvarmes til, så nitten passerer gennem hullet.
Eksempel 4
Nitten og pladen fra forrige øvelse placeres sammen i en ovn. Bestem, hvilken minimumstemperatur ovnen skal have for at stålnitten kan passere gennem hullet i aluminiumspladen.
Opløsning
I dette tilfælde vil både nitten og hullet blive udvidet. Men ekspansionskoefficienten for stål er α = 12 ∙ 10-6 (° C)-1, mens aluminium er α = 23 ∙ 10-6 (° C)-1 .
Vi ser derefter efter en endelig temperatur T, således at begge diametre falder sammen.
Hvis vi kalder nitten 1 og aluminiumpladen 2, ser vi efter en endelig temperatur T således at D1 = Dto.
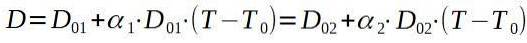
Hvis vi løser den endelige temperatur T, står vi tilbage med:
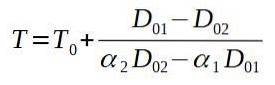
Derefter sætter vi de tilsvarende værdier.
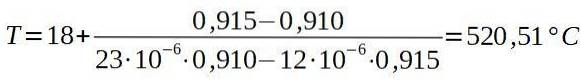
Konklusionen er, at ovnen skal være mindst 520,5 ° C for at nitten kan passere gennem hullet i aluminiumspladen.
Referencer
- Giancoli, D. 2006. Fysik: Principper med applikationer. Sjette udgave. Prentice Hall. 238-249.
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mac Graw Hill. 422-527.



Endnu ingen kommentarer