
Diametersymboler og formler, hvordan man får det, omkreds
Det diameter Det er den lige linje, der passerer gennem midten af en lukket flad kurve eller en figur i to eller tre dimensioner, og som også forbinder dets modsatte punkter. Normalt er det en omkreds (en flad kurve), en cirkel (en flad figur), en kugle eller en højre cirkulær cylinder (tredimensionelle objekter).
Selvom omkreds og cirkel normalt tages som synonymer, er der en forskel mellem de to udtryk. Omkredsen er den lukkede kurve, der omslutter cirklen, der opfylder den betingelse, at afstanden mellem et af dens punkter og centrum er den samme. Denne afstand er ingen ringere end omkredsen. I stedet er cirklen en plan figur afgrænset af omkredsen.

I tilfælde af omkreds, cirkel og kugle er diameteren et lige segment, der indeholder mindst tre punkter: centrum plus to punkter på kanten af omkredsen eller cirklen eller kuglens overflade.
Og hvad angår den højre cirkulære cylinder, henviser diameteren til tværsnittet, som sammen med højden er dets to karakteristiske parametre.
Diameteren af omkredsen og cirklen, symboliseret med ø eller simpelthen bogstavet “D” eller “d”, er relateret til dens omkreds, kontur eller længde, som er betegnet med bogstavet L:
L = π.D = π. eller
Så længe der er en omkreds, er kvotienten mellem dens længde og dens diameter det irrationelle tal π = 3.14159 ... på denne måde:
π = L / D
Artikelindeks
- 1 Sådan får du diameteren?
- 1.1 Figurer med konstant bredde
- 2 Diameter af en cirkel
- 2.1 - Eksempel 1
- 2.2 - Eksempel 2
- 3 Hvor mange diametre har en omkreds?
- 4 Referencer
Sådan får du diameteren?
Når du har tegningen af omkredsen eller cirklen eller direkte den cirkulære genstand, f.eks. En mønt eller en ring, er det meget let at finde diameteren med en lineal. Du skal bare sørge for, at linealens kant berører to punkter på omkredsen og midten af den på samme tid..
En tykkelse, vernier eller tykkelse er meget velegnet til måling af udvendige og indvendige diametre på mønter, bøjler, ringe, møtrikker, rør og mere..

Hvis der er data som f.eks. Radius i stedet for objektet eller tegningen deraf R, multipliceres derefter med 2 har vi diameteren. Og hvis længden eller omkredsen af omkredsen er kendt, kan diameteren også kendes ved at rydde:
D = 2.R
D = L / π
En anden måde at finde diameteren på er ved at kende arealet af cirklen, den sfæriske overflade, tværsnittet af cylinderen, det krumme område af cylinderen eller volumenet af kuglen eller cylinderen. Det hele afhænger af, hvilken geometrisk figur det er. For eksempel er diameter involveret i følgende områder og volumener:
-Cirkelområde: π. (D / 2)to
-Sfærisk overfladeareal: 4π. (D / 2)to
-Kuglens volumen: (4/3) π. (D / 2)3
-Højre cirkulære cylindervolumen: π. (D / 2)to.H (H er cylinderens højde)
Konstant bredde tal
Cirklen er en flad figur med konstant bredde, for hvor som helst man ser på den, er bredden diameteren D. Imidlertid er der andre måske mindre kendte figurer, hvis bredde også er konstant..
Lad os først se, hvad der forstås af bredden på en figur: det er afstanden mellem to parallelle linjer -støtterelinjer-, som igen er vinkelret på den givne retning, og som fængsler figuren, som vist i det venstre billede:
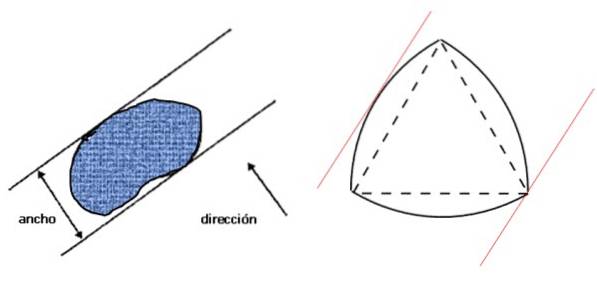
Ved siden af højre er Reuleaux-trekanten, som er en figur med konstant bredde, og som opfylder den betingelse, der er angivet i den venstre figur. Hvis figurens bredde er D, er dens omkreds givet af Barbiers sætning:
L = π.D
Kloakerne i byen San Francisco i Californien er formet som en Reuleaux-trekant, opkaldt efter den tyske ingeniør Franz Reuleaux (1829 - 1905). På denne måde kan dækslerne ikke falde gennem hullet, og der bruges mindre materiale til at fremstille dem, da deres areal er mindre end cirkelens areal:
A = (1- √3) .πDto = 0,705.Dto
Mens du er i en cirkel:
A = π. (D / 2)to = (π / 4) Dto= 0,785.Dto
Men denne trekant er ikke den eneste figur med konstant bredde. Du kan bygge den såkaldte Reuleaux polygoner med andre polygoner, der har et ulige antal sider.
Diameter af en omkreds

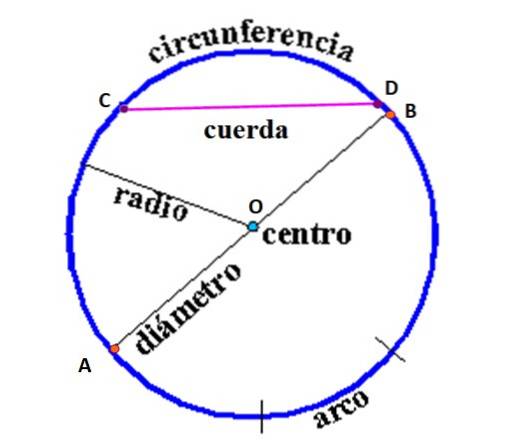
I den næste figur er elementerne i omkredsen defineret som følger:
Snor: linjesegment, der forbinder to punkter på omkredsen. I figuren er akkorden, der forbinder punkterne C og D, men der kan tegnes uendelige akkorder, der forbinder ethvert par punkter på omkredsen.
Diameter: det er akkorden, der passerer gennem midten og forbinder to punkter i omkredsen med centrum O. Det er den længste akkord i en omkreds, af den grund kaldes det "major akkord".
Radio: linjesegment, der forbinder centrum med ethvert punkt på omkredsen. Dens værdi, ligesom diameteren, er konstant.
Omkreds: er sættet med alle punkter lige langt fra O.
Sløjfe: defineret som et omkreds segment afgrænset af to radier (ikke tegnet i figuren).
- Eksempel 1
Det viste rektangel er 10 tommer højt, som når det rulles danner en højre cirkulær cylinder, hvis diameter er 5 tommer. Svar på følgende spørgsmål:
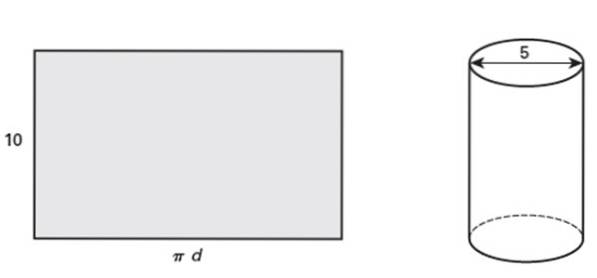
a) Hvad er rørets kontur?
b) Find arealet af rektanglet
c) Beregn cylinderens tværsnitsareal.
Løsning til
Rørets omrids er L = π.D = 5π in = 15,71 in.
Løsning b
Arealet af rektanglet er base x højde, er basen L, der allerede er beregnet, og højden er 10 tommer i henhold til udsagnet, derfor:
A = 15,71 tommer x 10 tommer = 157,1 tommerto.
Løsning c
Endelig beregnes det ønskede område således:
A = π. (D / 2)to = (π / 4) Dto = (π / 4) x (5 tommer)to= 19,63 tommerto.
- Eksempel 2
Beregn det skraverede område i figur 5a. Pladsen har side L.
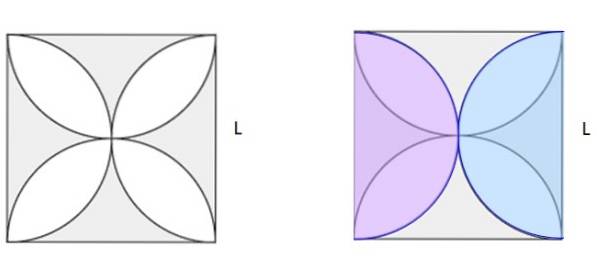
Opløsning
I figur 5b er to halvcirkler af samme størrelse tegnet i lyserød og blå, overlejret den originale figur. Mellem dem laver de en komplet cirkel. Hvis du finder kvadratområdet og trækker cirkelområdet, skal du lave det skraverede område i figur 5b. Og når man ser nøje, viser det sig, at det er halvdelen af det skyggefulde område i 5a.
-Firkantet område: L.to
-Halvcirkel Diameter: L
-Cirkelareal: π. (L / 2)to= (π / 4) L.to
-Forskel mellem områder = halvdelen af det skraverede område =
Lto - (π / 4) Lto = [(4 - π) / 4] L.to= 0,2146 Lto
-Skraveret område = 2 x 0,2146 Lto= 0,4292L2
Hvor mange diametre har en omkreds?
Uendelige diametre kan tegnes på en omkreds, og enhver af dem måler det samme.
Referencer
- Antonio. Reuleaux-trekanter og andre kurver med konstant bredde. Gendannet fra: divulgators.com.
- Baldor, A. 2002. Plane and Space Geometry and Trigonometry. Patria Cultural Group.
- Jiménez, R. Mathematics II. Geometri og trigonometri. 2. plads Udgave. Pearson.
- Wikipedia. Reuleaux trekant. Gendannet fra: es.wikipedia.org.
- Wolfram MathWorld. Diameter. Gendannet fra: mathworld.wolfram.com.


Endnu ingen kommentarer