
Ellipsoide egenskaber og eksempler
Det ellipsoid er en overflade i rummet, der hører til gruppen af kvadratiske overflader, og hvis generelle ligning er af formen:
Økseto + Vedto + Czto + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0
Det er den tredimensionelle ækvivalent af en ellipse, der er karakteriseret ved at have elliptiske og cirkulære spor i nogle specielle tilfælde. Spor er kurverne opnået ved at krydse ellipsoiden med et plan.

Ud over ellipsoiden er der fem kvadrater mere: hyperboloid med én ark og to ark, to typer paraboloid (hyperbolsk og elliptisk) og den elliptiske kegle. Dens spor er også koniske.
Ellipsoiden kan også udtrykkes ved hjælp af standardligningen i kartesiske koordinater. En ellipsoid centreret ved oprindelsen (0,0,0) og udtrykt på denne måde ligner ellipsen, men med et yderligere udtryk:

Værdierne af til, b Y c er reelle tal større end 0 og repræsenterer de tre halvakser af ellipsoiden.
Artikelindeks
- 1 Egenskaber ved ellipsoiden
- 1.1 - Standardligning
- 1.2 - Parametriske ligninger af ellipsoiden
- 1.3 - Spor af ellipsoiden
- 1.4 - Volumen
- 2 Særlige tilfælde af ellipsoiden
- 2.1 Reference ellipsoid
- 2.2 Numerisk eksempel
- 3 Referencer
Ellipsoide egenskaber
- Standardligning
Standardligningen i kartesiske koordinater for ellipsen centreret på punktet (h, k, m) det er:

- Parametriske ligninger af ellipsoiden
I sfæriske koordinater kan ellipsoiden beskrives som følger:
x = en synd θ. cos φ
y = b sin θ. sen φ
z = c cos θ
Halvakserne af ellipsoiden forbliver a, b og c, mens parametrene er vinklerne θ og φ i følgende figur:

- Spor af ellipsoiden
Den generelle ligning af en overflade i rummet er F (x, y, z) = 0 og sporene af overfladen er kurverne:
- x = c; F (c, y, z) = 0
- y = c; F (x, c, z) = 0
- z = c; F (x, y, c) = 0
I tilfælde af en ellipsoid er sådanne kurver ellipser og undertiden cirkler.
- Bind
Volumen V for ellipsoiden er givet ved (4/3) π gange produktet af dets tre halvakser:
V = (4/3) π. abc
Særlige tilfælde af ellipsoiden
-En ellipsoid bliver en kugle, når alle halvakserne har samme størrelse: a = b = c ≠ 0. Dette giver mening, da ellipsoiden er som en kugle, der er strakt forskelligt langs hver akse..
-Sfæroid er en ellipsoid, hvor to af halvakserne er identiske, og den tredje er forskellig, for eksempel kan det være a = b ≠ c.
Sfæroid kaldes også en ellipsoid af revolution, fordi den kan genereres ved at rotere ellipser omkring en akse.
Hvis rotationsaksen falder sammen med hovedaksen, er sfæroiden prolate, men hvis det falder sammen med den mindre akse, er det oblate:

Mål for fladering af sfæroiden (ellipticitet) er givet ved længdeforskellen mellem de to halvakser, udtrykt i brøkform, det vil sige, det er enhedens udfladning, givet ved:
f = (a - b) / a
I denne ligning repræsenterer a den halv-store akse og b den semi-mindre akse, husk at den tredje akse er lig med en af disse for en sfæroid. Værdien af f er mellem 0 og 1, og for en sfæroid skal den være større end 0 (hvis den var lig med 0, ville vi simpelthen have en sfære).
Referencen ellipsoid
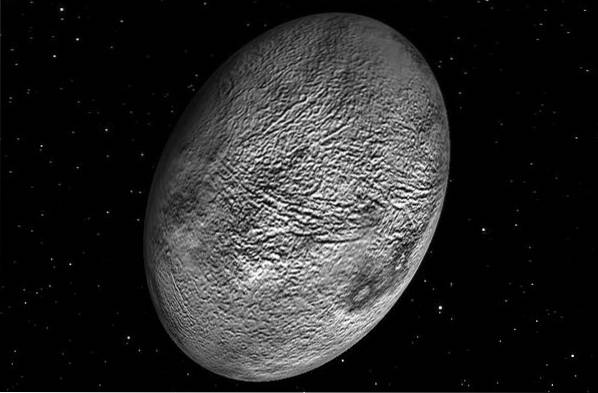
Planeterne og stjernerne generelt er normalt ikke perfekte kugler, fordi rotationsbevægelsen omkring deres akser flader kroppen ved polerne og buler den ud ved ækvator..
Det er derfor, Jorden viser sig at være som en oblat-sfæroid, omend ikke så overdrevet som den i den foregående figur, og for sin del er gasgiganten Saturn den fladeste af planeterne i solsystemet.
Så en mere realistisk måde at repræsentere planeterne på er at antage, at de er som en sfæroid eller ellipsoid af revolution, hvis halv-store akse er ækvatorialradius og den semi-mindre akse den polære radius..
Omhyggelige målinger foretaget på kloden har gjort det muligt at bygge reference ellipsoid af Jorden som dens mest præcise måde at arbejde den matematisk på.
Stjernerne har også rotationsbevægelser, der giver dem mere eller mindre flade former. Den hurtige stjerne Achernar, den ottende lyseste stjerne på nattehimlen, i den sydlige konstellation Eridanus er bemærkelsesværdigt elliptisk sammenlignet med de fleste. Der er 144 lysår fra os.
På den anden ekstrem side fandt forskere for et par år siden det mest sfæriske objekt, der nogensinde er fundet: stjernen Kepler 11145123, 5000 lysår væk, dobbelt så stor som vores sol og en forskel mellem halvakserne på kun 3 km. Som forventet spinder det også langsommere.
Hvad jorden angår, er den heller ikke en perfekt sfæroid på grund af dens robuste overflade og lokale variationer i tyngdekraften. Derfor er der mere end én referencekugleform tilgængelig, og på hvert sted vælges det mest passende for den lokale geografi..
Hjælp fra satellitter er uvurderlig til at skabe mere og mere nøjagtige modeller af jordens form, takket være dem er det f.eks. Kendt, at sydpolen er tættere på ækvator end nordpolen..
Numerisk eksempel
På grund af jordens rotation genereres der en centrifugalkraft, der giver den form af en aflang ellipsoid i stedet for en kugle. Jordens ækvatoriale radius vides at være 3963 miles, og den polære radius er 3942 miles..
Find ligningen af det ækvatoriale spor, den af denne ellipsoid og mål for dens udfladning. Sammenlign også med Saturns ellipticitet med nedenstående data:
-Saturns ækvatoriale radius: 60268 km
-Saturn Polar Radius: 54.364 km
Opløsning
Der kræves et koordinatsystem, som vi antager centreret om oprindelsen (Jordens centrum). Vi antager, at den lodrette z-akse og det spor, der svarer til ækvator, ligger på xy-planet, svarende til z = 0-planet.
I ækvatorialplanet er halvakserne a og b ens, derfor er a = b = 3963 miles, mens c = 3942 miles. Dette er et specielt tilfælde: en sfæroid centreret ved punktet (0,0,0) som angivet ovenfor.
Ækvatorialsporet er en cirkel med radius R = 3963 miles, centreret ved oprindelsen. Det beregnes ved at lave z = 0 i standardligningen:

Og standardligningen for den jordbaserede ellipsoid er:

F Jord = (a - b) / a = (3963-3942) miles / 3963 miles = 0,0053
F Saturn = (60268-54363) km / 60268 km = 0,0980
Bemærk, at ellipticiteten f er en dimensionsløs størrelse.
Referencer
- ArcGIS til desktop. Sfæroider og sfærer. Gendannet fra: desktop.arcgis.com.
- BBC World. Mysteriet med det mest sfæriske objekt, der nogensinde er opdaget i universet. Gendannet fra: bbc.com.
- Larson, R. Calculus and Analytical Geometry. Sjette udgave. Bind 2. McGraw Hill.
- Wikipedia. Ellipsoid. Gendannet fra: en.wikipedia.org.
- Wikipedia. Sfæroid. Gendannet fra: en.wikipedia.org.


Endnu ingen kommentarer