
Gravitationsenergiformler, egenskaber, anvendelser, øvelser
Det tyngdekraftenergi Det er den, som en massiv genstand har, når den nedsænkes i tyngdefeltet produceret af en anden. Nogle eksempler på genstande med tyngdekraft er: æblet i træet, det faldende æble, månen, der kredser om jorden og jorden kredser om solen.
Isaac Newton (1642-1727) var den første til at indse, at tyngdekraften er et universelt fænomen, og at enhver genstand med masse i sit miljø producerer et felt, der er i stand til at producere en kraft på en anden.

Artikelindeks
- 1 Formler og ligninger
- 2 Karakteristika for tyngdekraftenergi
- 2.1 Gravitationsfelt og potentiale
- 3 applikationer
- 3.1 Jordens tyngdepotentiale
- 3.2 Potentiel energi nær jordoverfladen
- 4 Øvelser
- 4.1 Øvelse 1: Jordens tyngdekraft sammenbrud
- 4.2 Øvelse 2: Gravitationel sammenbrud og undslippe hastighed
- 4.3 Øvelse 3: Gravitationsenergi i æblet
- 5 Referencer
Formler og ligninger
Kraften, som Newton henviste til, er kendt som tyngdekraften og giver energi til det objekt, som det virker på. Newton formulerede loven om universel tyngdekraft som følger:
"Lad der være to punktobjekter med henholdsvis masserne m1 og m2, hver udøver en attraktiv kraft på den anden, der er proportional med produktet af deres masser og omvendt proportional med kvadratet på afstanden, der adskiller dem".
Gravitationsenergi ELLER forbundet med tyngdekraften F det er:

Et objekt, der er nedsænket i et tyngdefelt, har tyngdepotentialenergi ELLER og kinetisk energi K. Hvis der ikke er andre interaktioner, eller hvis de har ubetydelig intensitet, er den samlede energi OG af det nævnte objekt er summen af dens tyngdekraftsenergi plus dens kinetiske energi:
E = K + U
Hvis et objekt er i et tyngdefelt, og ingen andre dissipative kræfter er til stede, såsom friktion eller luftmodstand, så er den samlede energi OG er en størrelse, der forbliver konstant under bevægelse.
Kendetegn for tyngdekraftenergi
- Et objekt har tyngdepotentialenergi, hvis det kun er i nærværelse af tyngdefeltet produceret af en anden.
- Gravitationsenergien mellem to objekter øges, når adskillelsesafstanden mellem dem er større.
- Arbejdet udført af tyngdekraften er lig med og i modsætning til variationen i gravitationsenergien i den endelige position i forhold til dens oprindelige position..
- Hvis et legeme kun udsættes for tyngdekraftens virkning, er variationen i dets tyngdekraft lig med og i modsætning til variationen i dets kinetiske energi..
- Den potentielle energi af et masseobjekt m som er i en højde h med hensyn til jordens overflade er mgh gange større end den potentielle energi på overfladen g tyngdeacceleration for højder h meget mindre end den jordbaserede radius.
Gravitationsfelt og potentiale
Gravitationsfeltet g er defineret som tyngdekraften F pr. masseenhed. Det bestemmes ved at placere en testpartikel m på hvert punkt i rummet og beregne kvotienten mellem den kraft, der virker på testpartiklen divideret med værdien af dens masse:
g = F / m
Gravitationspotentialet V for et objekt med masse m er defineret som tyngdepotentialenergien for det objekt divideret med dets egen masse.
Fordelen ved denne definition er, at tyngdepotentialet kun afhænger af tyngdefeltet, så når potentialet er kendt V, tyngdekraftenergi ELLER af en masseobjekt m det er:
U = m.V

Ansøgninger
Gravitationspotentiel energi er den, der lagres af kroppe, når de er i et tyngdefelt.
For eksempel har vandet i en tank mere energi, da tanken er højere..
Jo højere tankhøjde, jo større er hastigheden på vandet, der forlader vandhanen. Dette skyldes det faktum, at vandets potentielle energi i tankens højde omdannes til vandets kinetiske energi ved vandhanens udløb..
Når der dæmmes vand på toppen af et bjerg, kan den potentielle energi udnyttes til at dreje elproduktionsturbiner..
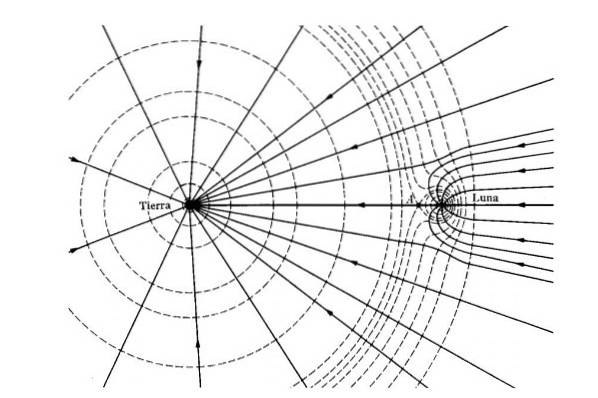
Gravitationsenergi forklarer også tidevandet. Da energi og tyngdekraften afhænger af afstand, er Månens tyngdekraft større på Jordens overflade tættest på Månen end ansigtet længst og modsat..
Dette giver en forskel i kræfter, der deformerer havets overflade. Effekten er større i en nymåne, når solen og månen er justeret.
Muligheden for at oprette rumstationer og satellitter, der forbliver relativt tæt på vores planet, skyldes tyngdekraft produceret af Jorden. Ellers ville rumstationer og kunstige satellitter strejfe gennem rummet.
Jordens tyngdepotentiale
Antag at Jorden har masse M og en genstand, der er over jordens overflade i det fjerne r med hensyn til centrum af det har masse m.
I dette tilfælde bestemmes tyngdepotentialet ud fra tyngdekraften ved blot at dividere med massen af objektet, hvilket resulterer:

Potentiel energi nær jordens overflade
Antag at Jorden har en radius RT og masse M.
Selvom Jorden ikke er et punktobjekt, svarer feltet på overfladen til det, der ville opnås, hvis al dens masse M blev koncentreret i midten, så tyngdekraften til et objekt i højden h over jordens overflade er
U (RT + h) = -G.M m (R.T + h) ^ - 1
Men fordi h er meget mindre end RT, ovenstående udtryk kan tilnærmes med
U = Uo + mgh
Hvor g er tyngdeacceleration, hvis gennemsnitlige værdi for Jorden er 9,81 m / s ^ 2.
Derefter er den potentielle energi Ep for et objekt med masse m i højden h over jordens overflade:
Ep (h) = U + Uo = mgh
På jordoverfladen h = 0, så et objekt på overfladen har Ep = 0. Detaljerede beregninger kan ses i figur 3.

Uddannelse
Øvelse 1: Jordens gravitationelle kollaps
Antag, at vores planet lider under tyngdekraft på grund af tab af termisk energi i dens indre, og dens radius falder til halvdelen af den nuværende værdi, men planetens masse forbliver konstant..
Bestem, hvad tyngdeaccelerationen nær den nye jordoverflade ville være, og hvor meget en overlevende, der vejer 50 kg-f, ville veje inden kollaps. Forøg eller mindsk personens tyngdekraft og med hvilken faktor.
Opløsning
Tyngdeaccelerationen på overfladen af en planet afhænger af dens masse og dens radius. Gravitationskonstanten er universel og fungerer lige meget for planeter og exoplaneter.
I det foreliggende tilfælde, hvis jordens radius reduceres med halvdelen, ville tyngdeaccelerationen på den nye jord være 4 gange større. Detaljer kan ses på det følgende tavle.

Dette betyder, at en supermand og overlevende, der vejede 50 kg-f på den gamle planet, vejer 200 kg-f på den nye planet..
På den anden side vil tyngdekraften være halveret på overfladen af den nye planet..
Øvelse 2: Gravitationel kollaps og flugthastighed
I forhold til situationen præsenteret i øvelse 1, hvad der ville ske med flugthastigheden: den øges, falder, med hvilken faktor?
Løsning 2
Escape-hastighed er den mindste hastighed, der er nødvendig for at undslippe tyngdekraften på en planet.
For at beregne det antages det, at et projektil, der affyres med denne hastighed, når uendeligt med nul hastighed. Desuden er gravitationsenergien ved uendelig nul. Derfor har et projektil, der affyres med flugthastighed, nul total energi.
Med andre ord, på planetens overflade på tidspunktet for skuddet skal summen af projektilens kinetiske energi + tyngdekraften være nul:
½ m Ve ^ 2 - (G M.m) / R.T = 0
Bemærk, at flugthastigheden ikke afhænger af projektilets masse, og dens værdi i kvadrat er
Ve ^ 2 = (2G M) / R.T
Hvis planeten kollapser til en radius halvdelen af originalen, bliver firkanten af den nye flugthastighed dobbelt.
Derfor vokser den nye flugthastighed og bliver 1,41 gange den gamle flugthastighed:
Gå '= 1,41 Gå
Øvelse 3: Gravitationsenergi i æblet
En dreng på balkonen i en bygning 30 meter over jorden smider et 250 g æble, der efter få sekunder når jorden.

a) Hvad er gravitationsenergiforskellen for æblet øverst i forhold til æblet på jordoverfladen?
b) Hvor hurtigt var æblet lige før det spildte på jorden?
c) Hvad sker der med energien, når æblet er fladt mod jorden?
Opløsning
a) Gravitationsenergiens forskel er
m.g.h = 0,250 kg * 9,81 m / s ^ 2 * 30 m = 73,6 J
b) Den potentielle energi, som æblet havde, da det var 30 m højt, omdannes til kinetisk energi, når æblet når jorden.
½ m v ^ 2 = m.g.h
v ^ 2 = 2.g.h
Ved at erstatte værdier og løse følger det, at æblet når jorden med en hastighed på 24,3 m / s = 87,3 km / t.
c) Naturligvis er æblet spredt, og al den gravitationelle energi, der er akkumuleret i starten, går tabt i form af varme, da stykkerne af æblet og stødzonen opvarmes, og desuden spredes en del af energien også i form af lyd bølger "sprøjt".
Referencer
- Alonso, M. (1970). Physics Vol. 1, Inter-American Educational Fund.
- Hewitt, Paul. 2012. Konceptuel fysik. 5. plads Ed. Pearson.
- Knight, R. 2017. Fysik for forskere og teknik: en strategi tilgang. Pearson.
- Sears, F. (2009). University Physics Vol. 1
- Wikipedia. Gravitationsenergi. Gendannet fra: es.wikipedia.com
- Wikipedia. Gravitationsenergi. Gendannet fra: en.wikipedia.com


Endnu ingen kommentarer