
Rotationsbalanceformler og ligninger, eksempler, øvelser

En udvidet krop angives at være i rotationsbalance når summen af drejningsmomenterne, der virker på den, er nul. Dette betyder ikke, at objektet nødvendigvis er i ro, men snarere at der ikke er nogen nettotendens til at ændre dets bevægelsestilstand for en anden..
Et objekt, der bevæger sig med konstant hastighed, gør det langs en lige linje, og vi kan betragte det i rotationsligevægt. Nu roterer objekter, fordi der er kræfter, der virker på dem på en sådan måde, at der opnås en rotation. Evnen hos en kraft til at producere rotation, kaldet moment eller torca, afhænger ikke kun af kraftens intensitet, men også af, hvor den påføres.

Vi genkender dette med det samme, når en lukket dør skal åbnes: kraft påføres aldrig nær hængslerne, men væk fra dem, det er derfor, håndtaget placeres så langt som muligt på den modsatte side af døren.
Dørens rotationsakse passerer gennem hængslerne. At insistere på at skubbe det meget tæt på hængslerne kræver en stor indsats for at få døren til at bevæge sig lidt..
I litteraturen findes moment under forskellige navne: moment, torsion, moment af en kraft og moment. De er alle synonyme.
Så vi er nødt til at kende drejningsmomenterne, der virker på et objekt for at fastslå den roterende ligevægtsbetingelse.
Artikelindeks
- 1 Betingelse for rotationsligevægt
- 1.1 Moment eller moment af en kraft
- 2 Formler og ligninger
- 3 eksempler
- 4 Øvelse løst
- 5 Referencer
Rotationsligevægtstilstand
Den roterende ligevægtsbetingelse er:
Summen af alle de moment eller moment, der virker på en krop, beregnet i forhold til enhver akse, skal være nul.
Det pågældende objekt skal strækkes, da partikler pr. Definition kun har translationel ligevægt.
Der kan være kræfter, der påføres kroppen og stadig eksisterer rotationsligevægt, så længe kræfterne ikke får det til at rotere.
Der kan også være bevægelse, endda accelereret, men altid langs en lige linje, da ikke alle kræfter fremkalder moment. Disse vises, når kræfterne ikke alle handler i samme handlingslinje..
Moment eller moment af en kraft
Moment er betegnet med det græske bogstav τ, på fed skrift fordi det er en vektor, og derfor skelner vi den fra dens størrelse eller modul, som er en skalar. Det afhænger af den anvendte kraft F, vektor r der er rettet fra rotationsaksen O til kraftens påføringspunkt og endelig fra vinklen mellem disse to vektorer.
Vektorproduktet fastlægger det passende forhold mellem disse mængder:
τ = r x F
Og momentmodulet, betegnet uden fed skrift, er:
τ = r⋅F⋅sen θ
Hvor θ er vinklen mellem r Y F. Enhederne for drejningsmoment er simpelthen Nm i det internationale system.
På figuren er der en skruenøgle, som det er beregnet til at dreje en møtrik mod uret (mod uret). Til dette testes det med to kræfter FTIL Y FB.
FTIL er tættere på O og har en vektor rTIL eller kortere løftearm, derfor producerer den ikke så meget drejningsmoment som kraften FB, som har samme størrelse, men har en vektor rB større.
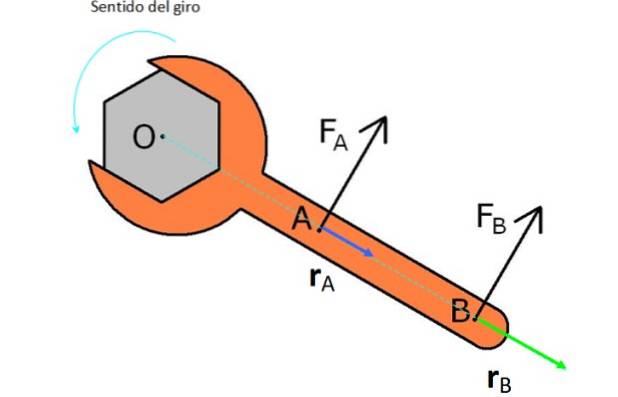
Bemærk, at hvis du vil dreje møtrikken med uret, skal du anvende kræfterne i den modsatte retning, som de vises i figuren.
Retning og følelse af drejningsmoment
Da momentet skyldes krydsproduktet mellem kraft- og positionsvektorerne, og disse er i skruenøglens plan, skal drejningsmomentet være en vektor, der er vinkelret på planet, dvs. rettet mod læseren eller mod indersiden af side.
Efter konvention er momentet positivt, hvis det roterer mod uret, og negativt, hvis det roterer med uret..
Retningen og følelsen af det resulterende drejningsmoment bestemmes let af den højre håndregel vist nedenfor:
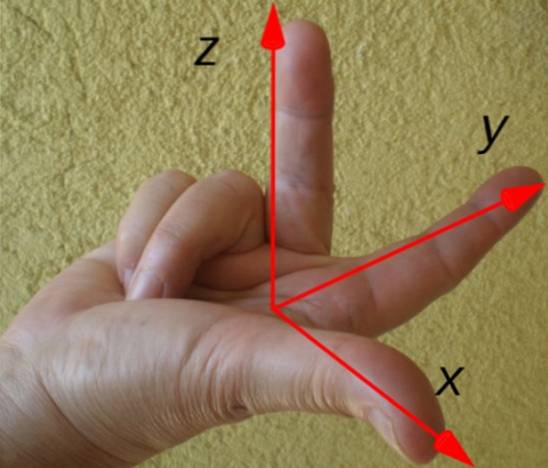
Pegefingeren peger i henhold til positionsvektoren r, langfinger efter styrke F og tommelfingeren peger retning og følelse af drejningsmoment τ. I dette eksempel er drejningsmomentet rettet langs x-aksen i henhold til koordinataksets tegning.
Formler og ligninger
Hvis drejningsmomenter virker på en krop τ1, τto, τ3 ... τjeg, nettet eller det resulterende drejningsmoment τn er vektorsummen af dem alle:
τn = τ1+ τto + τ3 +... τjeg
Med summeringsnotation forbliver det:
τn = ∑ τjeg
Ligevægtsbetingelsen udtrykkes matematisk som følger:
τn = 0
O brønd:
∑ τjeg = 0
Hvor momentet τ, med hensyn til en bestemt akse O beregnes den ved:
τ = r x F
Og hvis størrelse er:
τ = r⋅F⋅sen θ
Eksempler
-Hos mennesker og dyr er vægt en kraft, der kan forårsage drejningsmoment, dreje og falde.
Folk holder generelt en kropsholdning, så de holder dem i rotationsbalance, når de går, medmindre de praktiserer sportsaktiviteter, såsom gymnastik, skøjteløb eller sport generelt..
-To drenge, der formåede at forblive vandret i rocker eller op og ned er i rotationsligevægt.
-Når balancepanelerne er afbalancerede, er systemet i rotationsligevægt.
-Skilte og trafiklys, der hænger på gader og veje, er også i rotationsligevægt. Hvis kablerne, der holder dem, går i stykker, går denne balance tabt, og skiltet hænger eller falder..
-Hængebroer som Golden Gate i San Francisco og broen i figur 1.
Træning løst
Støttebjælken vist i figuren er meget lys. Styrken, der udøves af støtten, er F og ved ekstrem højre kraft anvendes TIL.
Det anmodes om at beregne størrelsen af disse kræfter i betragtning af at systemet er i translationel og rotationsligevægt.

Opløsning
Da systemet ikke bevæger sig, annulleres summen af kræfter. De er alle lodrette og kan bearbejdes i størrelsesorden. Den positive retning er opad, og den negative retning er nedad, derfor:
F - 80 - A = 0
Nu anvendes den roterende ligevægtsbetingelse, som vi skal vælge en vilkårlig rotationsakse for. I dette tilfælde vælges det yderst til højre, så vektoren rTIL er null, på denne måde drejningsmomentet udøves af TIL, men kun de af F og styrken fra venstre.
Momentet produceret af F er i henhold til højre håndregel og det viste koordinatsystem:
τF = rF x F = 0,9 F (-k) N.m
Det er rettet mod indersiden af skærmen og har et negativt tegn. Mens momentet produceret af 80 N kraften er:
τ = 80 x 1,20 (k) Nm = 96 (k) Nm
Dette drejningsmoment ledes væk fra skærmen og tildeles et positivt tegn. Hvordan der er rotationsligevægt:
96 - 0,9 ° F = 0
Størrelsen af F det er:
F = (96 / 0,9) N = 106,7 N
Og da systemet er i translationel ligevægt, annulleres summen af kræfterne. Dette giver os mulighed for at løse størrelsen på TIL:
F - A - 80 N = 0
Derfor:
A = 106,7 - 80 N = 26,7 N.
Referencer
- Rex, A. 2011. Grundlæggende fysik. Pearson.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7. Ed. Cengage Learning.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1. Pearson.
- Tipler, P. (2006) Fysik til videnskab og teknologi. 5. udg. Bind 1. Editorial Reverté.
- Tippens, P. 2011. Fysik: begreber og applikationer. 7. udgave. Mcgraw bakke.



Endnu ingen kommentarer