Konveks spejlkoncept, egenskaber, eksempler

Det konveks spejl eller divergerende er et buet spejl, næsten altid sfærisk i form og med den reflekterende overflade på den ydre side af sfæren, såsom juletræets ornamenter. Takket være konvekse spejle er det muligt at opnå en lang række billeder, afhængigt af hvor objektet er placeret, og det er grunden til, at de har så mange anvendelser.

For eksempel er spejle, der er anbragt i gaderne for at lette transit af køretøjer i smalle kryds, konvekse, da de producerer et billede med et bredt synsfelt.

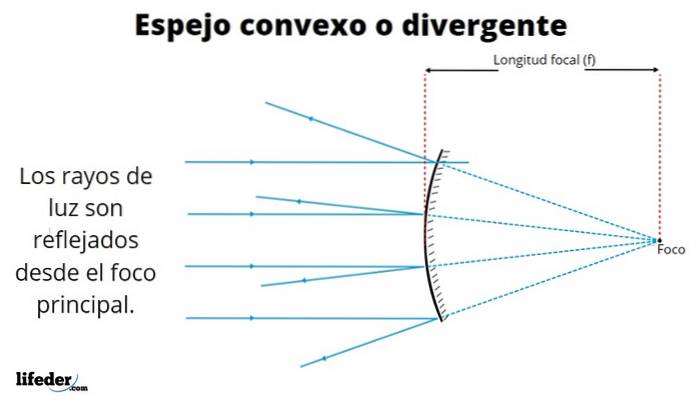
De således dannede billeder er forskellige afhængigt af det sted, hvor objektet er placeret. Billedet ovenfor viser de parallelle stråler fra en fjern kilde som solen..

Strålerne reflekteres i henhold til refleksionsloven, hvilket indikerer, at indstrålingsvinklen for strålen er den samme, som den reflekteres med. Som vi kan se, adskiller de reflekterede stråler sig - de krydser ikke - når de forlader den spekulære overflade, hvorfor denne form for spejl også er kendt som divergerende.

Når refleksionerne strækker sig bag spejlet - stiplede linjer i figuren - krydser de et punkt F kaldet fokus..

Artikelindeks

• 1 Karakteristika for konvekse spejle
• 2 Billeddannelse i det konvekse spejl
• 3 Eksempler og anvendelser
  • 3.1 Spejle for at forhindre trafikulykker
  • 3.2 Spejle til overvågning
  • 3.3 Bagspejle
  • 3.4 Cassegrain-teleskop
• 4 ligninger af det konvekse spejl
  • 4.1 Forstørrelse af spejlet
  • 4.2 Forholdet mellem objektet og dets billede i det konvekse spejl
• 5 Interessante emner
• 6 Referencer

Funktioner af konvekse spejle

Det konvekse spejl har følgende egenskaber (se billedet ovenfor):

-Spejlets bemærkelsesværdige punkter er:

• C centrum, som falder sammen med midten af ​​den kugle, som spejlet hører til.
• F fokus, hvor strålene reflekteret bag spejlet konvergerer.
• Dets toppunkt P, som svarer til midten af ​​den sfæriske overflade og er collinear med C og F.

-Har optisk akse eller hovedakse, som er linjen vinkelret på den spekulære overflade. Stråler, der kun rammer den optiske akse, reflekteres i samme retning.

-Midten af ​​den kugle, som spejlet hører til, er ved punkt C og r er dens radius. A C er kendt som krumningens centrum, mens r er han Krumningsradius og angiver hvor buet spejlet er: jo mindre r, mere forstærket er den konvekse form.

-Skæringspunktet for de reflekterede stråler er kendt som Fokuspunkt af spejlet. Afstanden mellem F og P er ca. r/to:

f = r / 2

Dette udtryk gælder for spejle, hvis størrelse er meget mindre end deres krumningsradius.

-Billedet, der dannes, er mindre og også virtuelt, da det er placeret bag spejlet, som vi vil se nedenfor..

Billeddannelse i det konvekse spejl

For at vide, hvad billedet dannes i det konvekse spejl, anvendes strålebehandlingen, som består i at repræsentere lysstrålerne, der forlader objektet ved hjælp af lige linjer.

Disse stråler reflekteres på spejloverfladen, og de reflekterede stråler tegnes også. Strålemetoden kan anvendes på enhver form for spejl, ikke kun konvekse.

Ved at forlænge de reflekterede stråler skærer de hinanden på et bestemt tidspunkt, og det er netop her, hvor billedet dannes. Forlængelserne af de reflekterede stråler, der kommer fra et udvidet objekt, såsom et træ, er vist i nedenstående figur med brudte linjer.

I figuren nedenfor trækkes tre stråler fra objektet, meget specielle og lette at tegne, såvel som deres refleksioner:

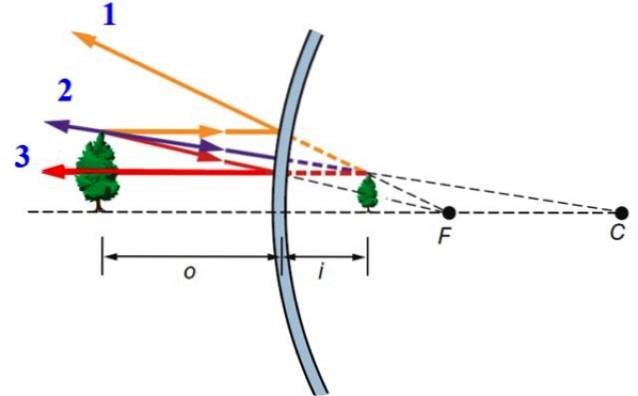
-Stråle 1, indfaldende parallelt med den optiske akse.

-Stråle 2, der falder på en sådan måde, at forlængelsen af ​​den reflekterede stråle passerer nøjagtigt gennem spejlets fokus, dvs. punkt F. Denne stråle reflekteres i en retning parallelt med den optiske akse.

-Endelig stråle 3, der ankommer vinkelret på den sfæriske overflade, og derfor reflekteres i samme retning.

I princippet anvendes denne procedure på hvert punkt i træet, men med den information, der er opnået fra de tre stråler, er det nok at finde billedet af objektet: det er dannet bag spejlet, det er lige og mindre end det original.

Eksempler og applikationer

Mange højpolerede sfæriske overflader fungerer som konvekse spejle, for eksempel skinnende og sølv julepynt såvel som skinnende nye stålskeer.

Også konvekse spejle har mange praktiske anvendelser, for eksempel:

Spejle for at forhindre trafikulykker

Konvekse spejle på gader og veje hjælper med at forhindre ulykker, da de giver dig mulighed for at se trafik komme fra hjørner.

Spejle til overvågning

Konvekse spejle bruges ofte i butikker og banker til at opdage tyve såvel som for at undgå kollisioner mellem mennesker og gaffeltrucks, der bevæger sig gennem gangene og mellem hylderne..

Bagspejle

Biler og motorcykler har konvekse bakspejle, der producerer lidt mindre billeder, men dækker mere synsfelt end flade spejle..

Cassegrain teleskop

Et af spejlene i det Cassegrain-reflekterende teleskop, det sekundære spejl, er konveks, selvom det ikke er sfærisk og tjener til at reflektere billedet mod teleskopets hovedspejl.

Konvekse spejlligninger

Lad os overveje de rigtige trekanter i den følgende figur, bestemt af stråle 1, der kommer fra pilens top, dens refleksion og dens forlængelse.

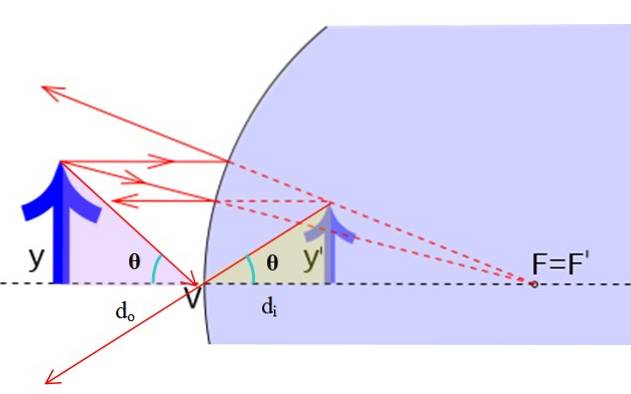
Det originale billede har højden y, mens højden på det virtuelle billede er y ' . Det er rigtigt, at:

tan θ = y / d_eller = y '/ d_jeg

Spejl forstørrelse

Forholdet mellem billedets højde og objektets højde er spejlforstørrelse, hvilket kaldes det, selvom det opnåede billede er mindre end det virkelige objekt. Vi betegner det med m:

m = y '/ y = d_jeg / d_eller

Forholdet mellem objektet og dets billede i det konvekse spejl

Lad os nu overveje denne anden figur, hvor AVF-regionen kan betragtes som en ret trekant, da spejlets krumning ikke er særlig fremhævet. Derfor:

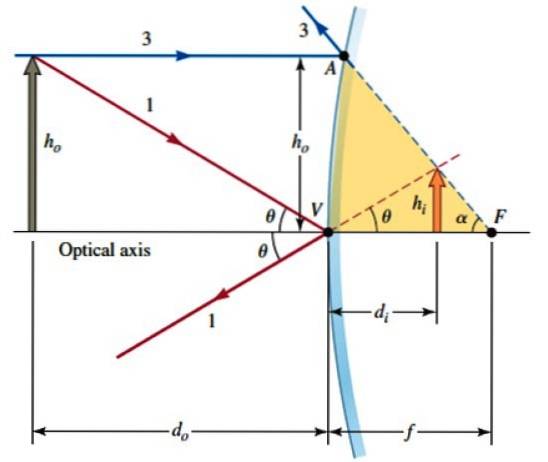
AV ≈ h_eller

Derefter:

tan α = h

1- (d_jeg / f) = d_jeg / d_eller

Ved at dividere alt med d_jeg:

Derfor, som F Y d_jeg er bag spejlet, er der placeret et minustegn foran dem, mens der for afstand d_eller det er ikke nødvendigt, da det er foran spejlet. Således er den tidligere ligning:

Temaer af interesse

Konkave spejl.

Referencer

1. Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 2. Mc Graw Hill.
2. Giambattista, A. 2010. Fysik. 2. plads Ed. McGraw Hill.
3. Katz, D. 2017. Fysik for forskere og ingeniører. Cengage læring.
4. Thomas, W. 2008. Konceptuel fysik. Mcgraw bakke.
5. Tippens, P. 2011. Fysik: begreber og applikationer. 7. udgave. Mcgraw bakke.