
Beskrivende statistikhistorie, karakteristika, eksempler, begreber
Det Beskrivende statistik er den gren af statistik, der er ansvarlig for at indsamle og organisere information om systemers opførsel med mange elementer, kendt generelt med navnet befolkning.
For at gøre dette bruger den numeriske og grafiske teknikker, hvorigennem den præsenterer information uden at forudsige eller slutte sig om den befolkning, hvorfra den kommer..

Artikelindeks
- 1 Historie
- 1.1 Ancient Age
- 1.2 Renæssance
- 1.3 Moderne tidsalder
- 2 Karakteristik af beskrivende statistik
- 3 Hvad er beskrivende statistik til?
- 3.1 Økonomi
- 3.2 Fysik og mekanik
- 3.3 Medicin
- 3.4 Ernæring
- 4 Eksempler på beskrivende statistikker
- 4.1 Eksempel 1
- 4.2 Eksempel 2
- 4.3 Eksempel 3
- 5 Grundlæggende begreber i beskrivende statistik
- 5.1 Befolkning
- 5.2 Prøve
- 5.3 Variabel
- 5.4 Foranstaltninger af central tendens
- 5.5 Dispersionsmålinger
- 6 Emner af interesse
- 7 Referencer
Historie
Alderdom
Statistik har sin oprindelse i det menneskelige behov for at organisere de nødvendige oplysninger for dets overlevelse og velbefindende samt at foregribe de begivenheder, der påvirker den. Antikens store civilisationer efterlod optegnelser over bosættere, opkrævet skat, mængde høst og størrelsen på hære.
For eksempel beordrede Ramses II (1279-1213 f.Kr.) under hans lange regeringstid en folketælling af lande og indbyggere i Egypten, som på det tidspunkt havde omkring 2 millioner indbyggere.
Bibelen fortæller ligeledes, at Moses foretog en folketælling for at finde ud af, hvor mange soldater de tolv stammer i Israel havde.
Også i det antikke Grækenland blev folk og ressourcer talt. Romerne, der var bemærkelsesværdige for deres høje organisation, registrerede regelmæssigt befolkningen og udarbejdede folketællinger hvert femte år inklusive territorier og ressourcer..
Renæssance
Efter Roms tilbagegang var vigtige statistiske optegnelser knappe, indtil ankomsten af renæssancen, da statistik genopstod som et hjælpemiddel i beslutningsprocessen.
I slutningen af det syttende århundrede blev teorien om sandsynligheder født, et resultat af folks tilbøjelighed til hasardspil, hvilket gav Statistik den matematiske strenghed, der gjorde det til en videnskab i sig selv.
Moderne tidsalder
En ny impuls kom med teorien om fejl og mindste kvadrater i det 19. århundrede, som blev fulgt af metoden til korrelation mellem variabler, for kvantitativt at vurdere forholdet mellem dem..
Indtil endelig i det 20. århundrede spredte statistik sig til hver gren af videnskab og teknik som et uundværligt værktøj til løsning af problemer..
Beskrivende statistiske egenskaber
Beskrivende statistikker er kendetegnet ved:
- Organiser de indsamlede oplysninger i form af data og grafer. Graferne kan være forskellige: blandt andet histogrammer, frekvenspolygoner, pieformede diagrammer..
- Fordel dataene i frekvensområder for at gøre det lettere at administrere dem. Brug aritmetik til at finde de mest repræsentative værdier af dataene gennem målinger af central tendens samt analysere deres spredning.
- Bestem formen på distributionerne, deres symmetri, hvis de er centreret eller skæv, og hvis de er spidse eller snarere flade.
Hvad er beskrivende statistik til?
Når data skal indsamles, organiseres og præsenteres, er beskrivende statistik vigtig inden for videnskabelige områder, der beskæftiger sig med mange elementer og mængder, såvel som i meget af menneskelige aktiviteter: økonomi, politik, sundhed, sport og meget mere..
Her er nogle eksempler:
Økonomi
Beskrivende statistik vedrører konsekvent registrering og organisering af data om befolkninger og deres alder, indkomst, investeringer, indtjening og udgifter. På denne måde planlægger regeringer og institutioner forbedringer og investerer ressourcer passende..
Med sin hjælp overvåges indkøb, salg, returnering og effektivitet af tjenester. Af denne grund er statistik afgørende for beslutningstagningen.
Fysik og mekanik
Fysik og mekanik bruger statistik til at studere kontinuerlige medier, der består af et stort antal partikler, såsom atomer og molekyler. Det viser sig, at det ikke er muligt at spore hver af dem separat..
Men når man studerer systemets globale opførsel (f.eks. En del gas) fra det makroskopiske synspunkt, er det muligt at finde gennemsnit og definere makroskopiske variabler for at kende deres egenskaber. Et eksempel på dette er den kinetiske teori om gasser.
Medicin
Det er et vigtigt redskab til overvågning af sygdomme, fra deres oprindelse og under deres udvikling, såvel som effektiviteten af behandlinger.
Statistikker, der beskriver sygdomsrater, kurhastigheder, inkubations- eller udviklingstider for en sygdom, den alder, som den normalt forekommer, og lignende data, er nødvendige, når man designer de mest effektive behandlinger..
Ernæring
En af de mange anvendelser af deskriptiv statistik er at registrere og bestille data om fødevareforbrug i forskellige populationer: dets mængde, kvalitet og hvilke der forbruges mest, blandt mange andre observationer, der interesserer eksperter..
Beskrivende statistiske eksempler
Her er nogle eksempler, der illustrerer, hvor nyttige beskrivende statistiske værktøjer er til at hjælpe med at træffe beslutninger:
Eksempel 1

Uddannelsesmyndighederne i et land planlægger institutionelle forbedringer. Antag at du vil implementere et nyt skoles kantinesystem.
Til dette er det nødvendigt at have data om den studerendes befolkning, for eksempel antallet af studerende pr. Klasse, deres alder, køn, højde, vægt og socioøkonomiske status. Disse oplysninger præsenteres derefter i form af tabeller og grafer..
Eksempel 2
For at holde styr på det lokale fodboldhold og foretage nye signeringer holder ledere styr på antallet af spillede spil, vundet, uafgjort og tabt samt antallet af mål, målscorerne og hvordan de formåede at score: frispark, halv domstol, sanktioner, med venstre eller højre ben, blandt andre detaljer.
Eksempel 3
En isbar har flere varianter af is og ønsker at forbedre sit salg, derfor foretager ejerne en undersøgelse, hvor de tæller antallet af kunder, de adskiller dem i grupper efter køn og aldersgruppe.
I denne undersøgelse registreres f.eks. Den yndlingsissmag og den bedst sælgende præsentation. Og med de indsamlede data planlægger de indkøb af smag og de beholdere og tilbehør, der er nødvendige for deres forberedelse..
Grundlæggende beskrivende statistik
Disse grundlæggende begreber er nødvendige for at anvende statistiske teknikker, lad os se:
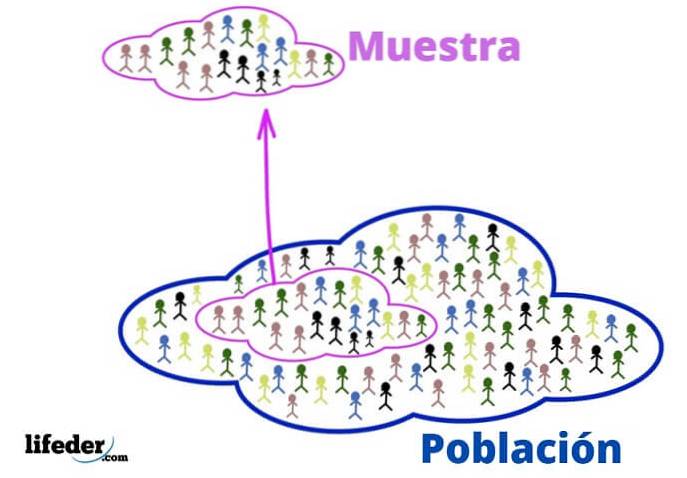
Befolkning
I den statistiske sammenhæng henviser befolkningen til det univers eller den gruppe, hvorfra oplysningerne kommer.
De handler ikke altid om mennesker, da de kan være grupper af dyr, planter eller genstande såsom biler, atomer, molekyler og endda begivenheder og ideer..
At vise
Når populationen er meget stor, trækkes der en repræsentativ prøve fra den og analyseres uden at miste relevant information..
Det kan vælges tilfældigt eller i henhold til nogle kriterier, som analytikeren tidligere har fastlagt. Fordelen er, at det at være en delmængde af befolkningen er meget mere håndterbart.
Variabel
Det henviser til det sæt værdier, som en bestemt karakteristik af befolkningen kan tage. En undersøgelse kan indeholde flere variabler, såsom alder, køn, vægt, akademisk niveau, civilstand, indkomst, temperatur, farve, tid og mange flere.
Variablerne kan være af forskellig art, så der er kriterier for at klassificere dem og give dem den mest passende behandling.
Kategoriske variabler og numeriske variabler
Afhængigt af måden, de måles på, kan variablerne være:
-Kategorisk
-Numerisk
Kategoriske variabler, også kaldet kvalitativ, repræsenterer kvaliteter såsom en persons civilstand, der kan være enlig, gift, skilt eller enke.
I stedet numeriske variabler eller kvantitativ, kan måles, såsom alder, tid, vægt, indkomst og mere.
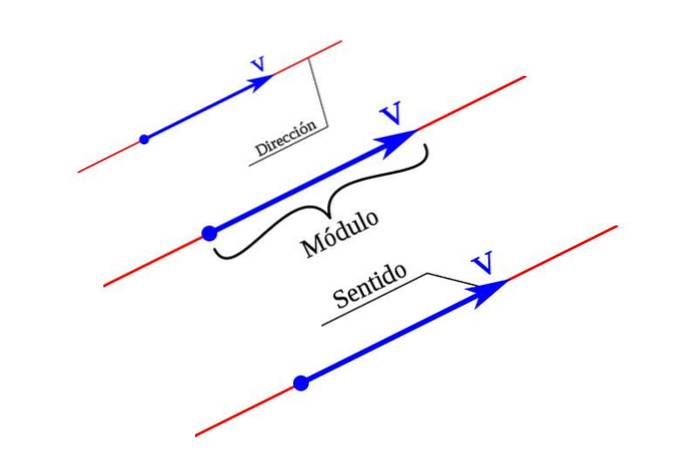
Diskrete variabler og kontinuerlige variabler
Diskrete variabler tager kun diskrete værdier, som deres navn antyder. Eksempler på dem er antallet af børn i en familie, hvor mange emner der er i et bestemt forløb og antallet af biler på en parkeringsplads.
Disse variabler tager ikke altid heltalsværdier, da der også er brøkdele.
På den anden side tillader kontinuerlige variabler uendelige værdier inden for et bestemt område, såsom en persons vægt, blodets pH, tidspunktet for en telefonkonsultation og diameteren af fodbold..
Foranstaltninger af central tendens
De giver en idé om den generelle tendens efterfulgt af dataene. Vi vil nævne de tre mest anvendte centrale foranstaltninger:
-Halvt
-Median
-mode
Halvt
Svarer til gennemsnittet af værdierne. Det beregnes ved at tilføje alle observationer og dividere med det samlede antal:

mode
Det er den værdi, der gentages mest i et datasæt, den mest eller den hyppigste, da der i en distribution kan være mere end en tilstand.
Median
Ved sortering af et datasæt er medianen den centrale værdi for dem alle.
Målinger af spredning
De påpeger dataens variabilitet og giver en idé om, hvor langt eller spredt de er fra de centrale mål. De mest anvendte er:
Rang
Det er forskellen mellem den største værdi xM og den mindste xm fra et datasæt:
Rang = xM - xm
Variation
Måler, hvor langt dataene er fra gennemsnitsværdien. For at gøre dette laves et gennemsnit, men med forskellene mellem enhver værdi xjeg og middelværdien, kvadrat for at forhindre dem i at fjerne hinanden. Det er normalt betegnet med det græske bogstav σ i kvadrat eller med sto:

Variansen har ikke de samme enheder som dataene, så standardafvigelsen er defineret som kvadratroden af variansen og betegnes som σ eller s:

I stedet for at tage hver enkelt data i betragtning, foretrækkes det at gruppere dem i intervaller, hvilket letter arbejdet, især hvis der er mange værdier. For eksempel, når man arbejder med børn i en skole, kan de grupperes i aldersgrupper: 0 til 6 år, 6 til 12 år og 12 til 18 år.
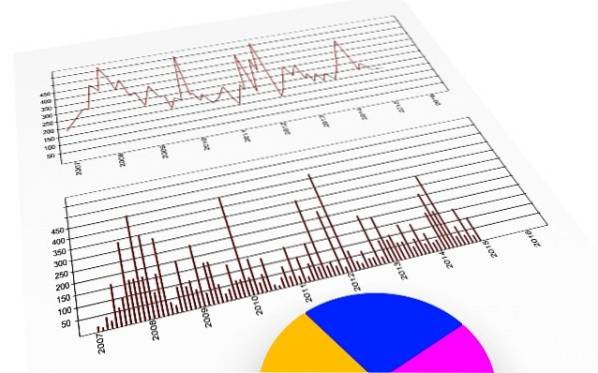
Diagrammer
De er en fantastisk måde at se distributionen af data på et øjeblik og indeholder alle de oplysninger, der er samlet i tabellerne og tabellerne, men meget mere overkommelige.
Der er et stort udvalg af dem: med søjler, lineære, cirkulære, stængler og blade, histogrammer, frekvens polygoner og piktogrammer. Eksempler på statistiske grafer er vist i figur 3..
Temaer af interesse
Filialer af statistikker.
Statistiske variabler.
Befolkning og prøve.
Inferential statistik.
Referencer
- Faraldo, P. Statistik og forskningsmetode. Gendannet fra: eio.usc.es.
- Fernández, S. 2002. Beskrivende statistik. 2. plads Udgave. ESIC redaktionelt. Gendannet fra: Google Bøger.
- Statistikhistorie. Gendannet fra: eumed.net.
- Ibañez, s. 2010. Matematik II. Kompetence tilgang. Cengage læring.
- Monroy, S. 2008. Beskrivende statistik. 1. Udgave. National Polytechnic Institute of Mexico.
- Universformler. Beskrivende statistik. Gendannet fra: universoformulas.com.


Endnu ingen kommentarer