
Tilfældigt eksperimentkoncept, prøveplads, eksempler
Der er tale om tilfældigt eksperiment når resultatet af hvert bestemt forsøg er uforudsigeligt, selv om sandsynligheden for forekomst af et bestemt resultat kan fastslås.
Det bør imidlertid præciseres, at det ikke er muligt at gengive det samme resultat af et tilfældigt system med de samme parametre og indledende betingelser i hvert forsøg i eksperimentet..

Et godt eksempel på et tilfældigt eksperiment er rulning af en matrice. Selv hvis man sørger for at rulle matricen på samme måde, vil hvert forsøg give et uforudsigeligt resultat. Faktisk er det eneste, der kan siges, at resultatet kan være et af følgende: 1, 2, 3, 4, 5 eller 6.
Kast af en mønt er et andet eksempel på et tilfældigt eksperiment med kun to mulige resultater: hoveder eller haler. Selvom mønten kastes fra samme højde og på samme måde, vil chancefaktoren altid være til stede, hvilket resulterer i usikkerhed ved hvert nyt forsøg..
Det modsatte af et tilfældigt eksperiment er et deterministisk eksperiment. For eksempel er det kendt, at kogetemperaturen er 100 ºC hver gang vand koges ved havoverfladen. Men det sker aldrig, at resultatet, når man holder de samme betingelser, undertiden er 90 ° C, andre 12 0 ° C og nogle gange 100 ° C..
Artikelindeks
- 1 Prøveplads
- 1.1 Begivenhed eller begivenhed
- 2 Eksempler
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 3 Referencer
Prøveplads
Sættet med alle mulige resultater af et tilfældigt eksperiment kaldes prøveplads. I det tilfældige eksperiment med at rulle en matrice er prøveområdet:
D = 1, 2, 3, 4, 5, 6.
På den anden side, i kastet af en mønt, er prøveområdet:
M = hoveder, stempel.
Begivenhed eller begivenhed
I et tilfældigt eksperiment, a begivenhed det er forekomsten eller ej af et bestemt resultat. For eksempel i tilfælde af en møntkast er en begivenhed eller begivenhed, at den kommer op hoveder.
En anden begivenhed i et tilfældigt eksperiment kunne være følgende: at et tal mindre end eller lig med tre rulles på rullen af en matrice.
Hvis begivenheden opstår, er sæt af mulige resultater sættet:
E = 1, 2, 3
Til gengæld er dette en delmængde af prøveområdet eller -sættet:
M = 1, 2, 3, 4, 5, 6.
Eksempler
Her er nogle eksempler, der illustrerer ovenstående:
Eksempel 1
Antag at to mønter kastes, den ene efter den anden. Det spørger:
a) Angiv, om det er et tilfældigt eksperiment eller tværtimod et deterministisk eksperiment.
b) Hvad er prøveområdet S for dette eksperiment?
c) Angiv begivenhedssættet A svarende til det faktum, at eksperimentet resulterer i hoveder og haler.
d) Beregn sandsynligheden for, at begivenhed A forekommer.
e) Find endelig sandsynligheden for, at begivenhed B opstår: ingen hoveder vises i resultatet.
Opløsning
a) Det er et tilfældigt eksperiment, fordi der ikke er nogen måde at forudsige, hvad der vil være resultatet af et kast af de to mønter.
b) Prøveområdet er sættet med alle mulige resultater:
S = (c, c), (c, s), (s, c), (s, s)
c) Begivenhed A, hvis den sker, kan have følgende resultater:
A = (c, s), (s, c)
d) Sandsynligheden for, at begivenhed A opstår, opnås ved at dividere antallet af elementer i sæt A med antallet af elementer i sæt S svarende til prøveområdet:
P (A) = 2/4 = ½ = 0,5 = 50%
e) Sættet af mulige resultater svarende til begivenhed B (vises ikke hoveder i resultatet) er:
B = (s, s)
Derfor er sandsynligheden for, at begivenhed B opstår i et forsøg kvotienten mellem antallet af mulige resultater af B og antallet af samlede tilfælde:
P (B) = ¼ = 0,25 = 25%.
Eksempel 2
En taske indeholder 10 hvide kugler og 10 sorte kugler. Tre kugler trækkes efter hinanden tilfældigt og uden at se indad.
a) Bestem prøveområdet for dette tilfældige eksperiment.
b) Bestem det sæt resultater, der svarer til begivenhed A, som består i at have to sorte kugler efter eksperimentet.
c) Begivenhed B er at opnå mindst to sorte kugler, bestem sæt B-resultater for denne begivenhed.
d) Hvad er sandsynligheden for, at begivenhed A finder sted?
e) Find sandsynligheden for, at begivenhed B opstår.
f) Bestem sandsynligheden for, at resultatet af det tilfældige eksperiment er, at du har mindst en sort marmor. Denne begivenhed kaldes C.

Løsning til
For at konstruere prøveområdet er det nyttigt at lave et trædiagram som det, der er vist i figur 3:
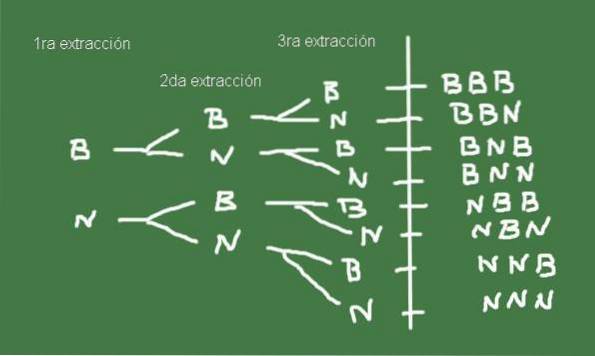
Sættet Ω af mulige resultater af udtrækning af tre kugler fra en pose med det samme antal sorte og hvide kugler er netop prøveområdet for dette tilfældige eksperiment.
Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n) , (n, n, b), (n, n, n)
Løsning b
Sættet af mulige resultater svarende til begivenhed A, som består af at have to sorte kugler, er:
A = (b, n, n), (n, b, n), (n, n, b)
Løsning c
Begivenhed B defineres som: “at have mindst to sorte kugler efter at have tilfældigt trukket tre af dem”. Sættet af mulige resultater for begivenhed B er:
B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)
Løsning d
Sandsynligheden for at have begivenhed A er kvotienten mellem antallet af mulige udfald for denne begivenhed og det samlede antal mulige udfald, det vil sige antallet af elementer i prøveområdet.
P (A) = n (A) / n (Ω) = 3/8 = 0,375 = 37,5%
Så der er en 37,5% chance for at have to sorte kugler efter tilfældig trækning af tre kugler fra posen. Men bemærk, at vi på ingen måde kan forudsige det nøjagtige resultat af eksperimentet.
Løsning e
Sandsynligheden for, at begivenhed B opstår, bestående af at opnå mindst en sort marmor, er:
P (B) = n (B) / n (Ω) = 4/8 = 0,5 = 50%
Dette betyder, at muligheden for, at begivenhed B sker, er lig med sandsynligheden for, at den ikke finder sted.
Løsning f
Sandsynligheden for at opnå mindst en sort marmor efter udvinding af tre af dem er lig med 1 minus sandsynligheden for, at resultatet er "de tre hvide kugler".
P (C) = 1 - P (b b b) = 1 - ⅛ = ⅞ = 0,875 = 87,5%
Nu kan vi kontrollere dette resultat ved at bemærke, at antallet af muligheder, som begivenheden C finder sted, er lig med antallet af elementer i de mulige resultater for begivenheden C:
C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) , (n, n, n)
n (C) = 7
P (C) = n (C) / n (Ω) = ⅞ = 87,5%
Referencer
- CanalPhi. Tilfældigt eksperiment. Gendannet fra: youtube.com.
- MateMovil. Tilfældigt eksperiment. Gendannet fra: youtube.com
- Pishro Nick H. Introduktion til sandsynlighed. Gendannet fra: probabilitycourse.com
- Ross. Sandsynlighed og statistik for ingeniører. Mc-Graw Hill.
- Wikipedia. Eksperiment (sandsynlighedsteori). Gendannet fra: en.wikipedia.com
- Wikipedia. Deterministisk begivenhed. Gendannet fra: es. wikipedia.com
- Wikipedia. Tilfældigt eksperiment. Gendannet fra: es.wikipedia.com



Endnu ingen kommentarer