Det statisk friktion er den kraft, der opstår mellem to overflader, når den ene overflade ikke glider i forhold til den anden. Det er meget vigtigt, da det giver os mulighed for at bevæge os fremad, når vi går, da det er kraften mellem gulvet og skoens sål.
Det er også statisk friktion, der vises mellem fortovet og bilens dæk. Hvis denne kraft ikke er til stede, er det umuligt for bilen at begynde at køre, som det sker i en bil, der forsøger at starte på en iset overflade: hjulene glider, men bilen bevæger sig ikke.
Statisk friktion afhænger af overfladenes ruhed i kontakt og også af typen af materiale, som de er fremstillet af. Derfor er dækkene og sportsskoene lavet af gummi for at øge friktionen med fortovet..
I den statiske friktionsmodel opsummeres materialernes egenskaber og graden af ruhed mellem overfladerne i et tal kaldet statisk friktionskoefficient, som bestemmes eksperimentelt.
Artikelindeks
Ovenstående figur viser en bog, der ligger i ro på et bord, der har en hældning på 15,7º.
Hvis bogens og bordets overflader var meget glatte og polerede, kunne bogen ikke stå stille. Men da de ikke er det, vises en kraft, der er tangent til overfladerne i kontakt kaldet kraften af statisk friktion.
Hvis hældningsvinklen er stor nok, er der ikke nok statisk friktionskraft for at afbalancere bogen, og den ville begynde at glide.
I dette tilfælde er der også friktion mellem bogen og bordet, men det ville være en styrke af dynamisk friktion, også kaldet kinetisk friktion.
Der er en grænse mellem statisk friktion og dynamisk friktion, som opstår, når den statiske friktion når sin maksimale værdi.
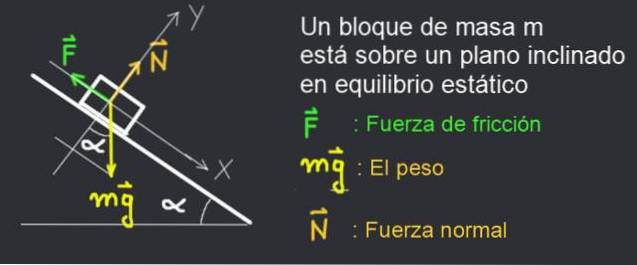
Lad os overveje i figur 2, kraftdiagrammet for en massebog m, der holdes i ro på et hældningsplan α.
Bogen forbliver i ro, fordi den statiske friktionskraft F afbalancerer systemet.
Hvis hældningsvinklen øges lidt, skal overfladerne i kontakt give mere friktionskraft, men mængden af statisk friktion, som overfladerne i kontakt kan give, har en maksimal grænse Fmaks, nemlig:
F ≤ Fmaks.
Den maksimale statiske friktionskraft vil afhænge af materialerne og graden af ruhed på overflader, der er i kontakt, samt grebets fasthed.
Den statiske friktionskoefficient μog er et positivt tal, der afhænger af egenskaberne ved overfladerne i kontakt. Normal kraft N at planet udøver på blokken viser graden af tæthed mellem blokens overflade og planet. Sådan bestemmer de den maksimale friktionskraft, som overflader giver, når der ikke glider:
Fmaks = μog N
Sammenfattende følger den statiske friktionskraft følgende model:
F ≤ μog N
Den statiske friktionskoefficient er et dimensionsløst tal, der bestemmes eksperimentelt for hvert overfladepar.
Vi betragter blokken i ro i figur 2. Følgende kræfter virker på den:
- Friktionskraft: F
- Vægten af masseblokken m: mg
- Normal kraft: N
Da blokken er i ro og ikke har nogen acceleration, er Newtons anden lov den resulterende kraft - en vektorsum - nul:
F + N + mg = 0
Et fast XY-koordinatsystem betragtes med X-aksen langs det skrånende plan og Y-aksen vinkelret på det, som vist i figur 2.
Kræfterne skal adskilles i henhold til deres kartesiske komponenter, hvilket giver anledning til følgende ligningssystem:
-Komponent X: -F + mg Sen (a) = 0
-Komponent Y: N - mg Cos (α) = 0
Værdien af den statiske friktionskraft løses fra den første ligning:
F = mg Sen (α)
Og fra det andet værdien af den normale kraft:
N = mg Cos (a)
Den statiske friktionskraft F overholder følgende model:
F ≤ μog N
Udskiftning af de tidligere opnåede værdier i den ulighed, vi har:
mg Sen (α) ≤ μog mg Cos (α)
Under hensyntagen til, at for værdier på α mellem 0º og 90º, er sinus- og cosinusfunktionerne begge positive, og at kvotienten mellem sinus og cosinus er tangenten, har vi:
Tan (α) ≤ μog
Ligestillingen gælder for en bestemt værdi af α kaldet den kritiske vinkel, og som vi betegner med α *, det vil sige:
μog = Tan (α *)
Den kritiske vinkel bestemmes eksperimentelt og øger gradvist hældningen, indtil den rigtige vinkel, hvormed blokken begynder at glide, dvs. den kritiske vinkel α *.
I bogen i figur 1 blev denne vinkel bestemt eksperimentelt, hvilket resulterede i 24 °. Derefter er koefficienten for statisk friktion:
μog = Tan (24º) = 0,45.
Det er et positivt tal mellem 0 og uendelig. Hvis μog = 0 overfladerne er perfekt glatte. Hvis μog → ∞ overfladerne er perfekt forbundet eller svejset.
Generelt er værdien af friktionskoefficienten mellem 0 og 10.
I sprint- eller dragsterløb opnås accelerationer på op til 4 g under starten, hvilket opnås nøjagtigt når dækkene ikke glider i forhold til fortovet..
Dette skyldes, at den statiske friktionskoefficient altid er større end den dynamiske friktionskoefficient..
Hvis vi antager, at køretøjets samlede vægt plus føreren er 600 kg, og at baghjulene understøtter 80% af vægten, skal du bestemme kraften for statisk friktion under start på 4 g og statisk friktionskoefficient mellem dækkene og fortovet..
Ifølge Newtons anden lov er den resulterende kraft lig med køretøjets samlede masse gange den acceleration, den får.
Da køretøjet er i lodret ligevægt, annulleres det normale og vægten, hvilket efterlader en friktionskraft F, som fortovet udøver på trækhjulens kontaktområde, hvilket efterlader:
F = m (4g) = 600 kg (4 x 9,8 m / sto) = 23520 N = 2400 kg-f
Dette betyder, at trækkraften er 2,4 ton.
Friktionskraften, som hjulet udøver på jorden, går baglæns, men dets reaktion, som er den samme og modsatte, virker på dækket og går fremad. Det er den kraft, der driver køretøjet.
Selvfølgelig produceres al denne kraft af motoren, der forsøger at skubbe gulvet tilbage gennem hjulet, men hjulet og gulvet er koblet af friktionskraft.
For at bestemme koefficienten for statisk friktion bruger vi det faktum, at den opnåede F er den maksimalt mulige friktion, da vi er på grænsen for maksimal acceleration, derfor:
F = μog N = μe (0,8 mg)
Det blev taget i betragtning, at baghjulene understøtter 0,8 gange vægten. Løsning af friktionskoefficienten opnår vi:
μog = F / (0,8 mg) = 23520 N / (0,8 x 600 kg x 9,8 m / s ^ 2) = 5.
Konklusion: μog = 5.
Endnu ingen kommentarer