
Konstant funktionsegenskaber, eksempler, øvelser
Det konstant funktion er den værdi, hvor værdien af y holdes konstant. Med andre ord: en konstant funktion har altid formen f (x) = k, hvor k er et reelt tal.
Ved graftegning af den konstante funktion i koordinatsystemet xy, resulterer altid i en lige linje parallelt med den vandrette akse eller akse x.
Denne funktion er et særligt tilfælde af affin funktion, hvis graf også er en lige linje, men med en hældning. Den konstante funktion har nul hældning, dvs. det er en vandret linje, som vist i figur 1.
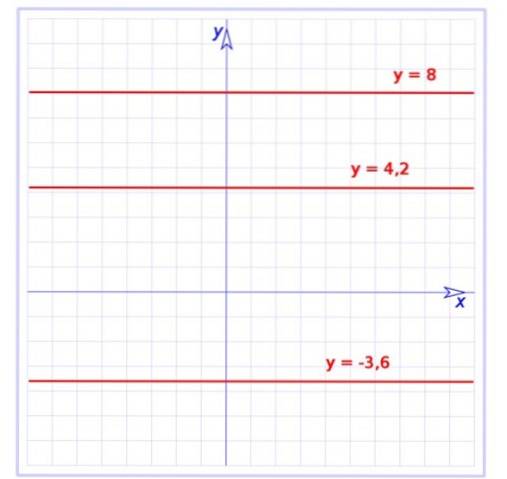
Der vises grafen over tre konstante funktioner:
f (x) = -3,6
g (x) = 4,2
h (x) = 8
Alle er linjer, der er parallelle med den vandrette akse, den første er under aksen, mens resten er over.
Artikelindeks
- 1 Karakteristika for den konstante funktion
- 2 Eksempler
- 2.1 En anden måde at repræsentere en konstant funktion på
- 3 Løst øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 3.3 - Øvelse 3
- 3.4 - Øvelse 4
- 3.5 - Øvelse 6
- 4 Referencer
Karakteristika for den konstante funktion
Vi kan opsummere de vigtigste egenskaber ved den konstante funktion som følger:
-Grafen er en lige vandret linje.
-Det har et enkelt kryds med aksen Y, værdi k.
-Er kontinuerlig.
-Domænet for den konstante funktion (det sæt af værdier, som x) er sættet med reelle tal R.
-Stien, området eller kontradomænet (det sæt af værdier, som variablen tager Y) er simpelthen den konstante k.
Eksempler
Funktioner er nødvendige for at etablere forbindelser mellem mængder, der på en eller anden måde afhænger af hinanden. Forholdet mellem dem kan matematisk modelleres for at finde ud af, hvordan en af dem opfører sig, når den anden varierer..
Dette hjælper med at opbygge modeller til mange situationer og forudsige deres adfærd og udvikling..
På trods af sin tilsyneladende enkelhed har den konstante funktion mange anvendelser. For eksempel når det kommer til at studere størrelser, der forbliver konstante over tid eller i det mindste i en mærkbar tid.
På denne måde opfører størrelser sig i situationer som følgende:
-Det hastighed krydser en bil, der kører ned ad en lang lige motorvej. Så længe du ikke bremser eller accelererer, har bilen en ensartet lodret bevægelse.

-En fuldt opladet kondensator frakoblet et kredsløb har en belastning konstant i tiden.
-Endelig opretholder en fast parkeringsplads en pris konstant uanset hvor længe en bil er parkeret der.
En anden måde at repræsentere en konstant funktion på
Den konstante funktion kan alternativt repræsenteres som følger:
f (x) = kx0
Da enhver værdi af x hævet til 0 giver 1 som et resultat, reducerer det foregående udtryk til det allerede velkendte:
f (x) = k
Selvfølgelig sker det så længe værdien af k er forskellig fra 0.
Derfor er den konstante funktion også klassificeret som en polynomfunktion af grad 0, da eksponenten for variablen x er 0.
Løst øvelser
- Øvelse 1
Svar på følgende spørgsmål:
a) Kan det siges, at linjen givet ved x = 4 er en konstant funktion? Årsag til dit svar.
b) Kan en konstant funktion have en x-skæring?
c) Er funktionen f (x) = w konstantto?
Svar til
Her er grafen for linjen x = 4:
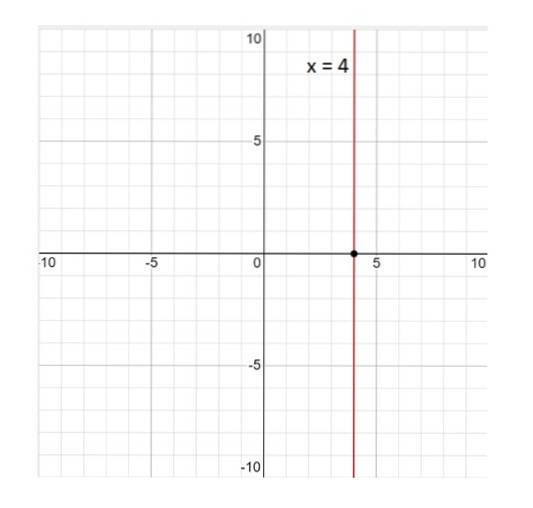
Linjen x = 4 er ikke en funktion; pr. definition er en funktion en sådan relation, at ved hver værdi af variablen x svarer til en enkelt værdi på Y. Og i dette tilfælde er dette ikke sandt, da værdien x = 4 er forbundet med uendelige værdier af Y. Derfor er svaret nej.
Svar b
Generelt har en konstant funktion intet skæringspunkt med aksen x, medmindre det handler om y = 0, i hvilket tilfælde det er aksen x Korrekt sagt.
Svar c
Ja, siden w er konstant, ligesom dens firkant. Det der betyder noget er det w afhænger ikke af inputvariablen x.
- Øvelse 2
Find krydset mellem funktionerne f (x) = 5 Y g (x) = 5x - 2
Opløsning
For at finde skæringspunktet mellem disse to funktioner kan de omskrives henholdsvis som:
y = 5; y = 5x - 2
De udlignes og opnår:
5x - 2 = 5
Hvad er en lineær ligning af første grad, hvis løsning er:
5x = 5 + 2 = 7
x = 7/5
Skæringspunktet er (7 / 5,5).
- Øvelse 3
Vis, at afledningen af en konstant funktion er 0.
Opløsning
Fra definitionen af derivat har vi:

f (x + h) = k
Udskiftning i definitionen:

Også, hvis vi tænker på derivatet som ændringshastigheden dy / dx, den konstante funktion gennemgår ingen ændringer, derfor er dens afledte nul.
- Øvelse 4
Find den ubestemte integral af f (x) = k.
Opløsning

En mobiltelefonvirksomhed tilbyder ubegrænset fast internet-service til $ 15 pr. Måned. Hvad er prisfunktionen i henhold til tid?
Opløsning
Lad P være den pris, der skal betales i $ og t den tid, der kan udtrykkes i dage. Funktionen er indstillet således:
P (t) = 15
- Øvelse 6
Den følgende graf over hastighed versus tid svarer til bevægelsen af en partikel.

Det spørger:
a) Skriv et udtryk for hastighedsfunktionen som en funktion af tiden v (t).
b) Find den tilbagelagte afstand fra mobilen i tidsintervallet mellem 0 og 9 sekunder.
Løsning til
Fra den viste graf kan det ses, at:
-v = 2 m / s i tidsintervallet mellem 0 og 3 sekunder
-Mobilen stoppes mellem 3 og 5 sekunder, da hastigheden i dette interval er 0.
-v = - 3 m / s mellem 5 og 9 sekunder.
Det er et eksempel på en stykkevis funktion eller stykkevis funktion, som igen er sammensat af konstante funktioner, der kun er gyldige i de angivne tidsintervaller. Det konkluderes, at den søgte funktion er:

Løsning b
Fra v (t) -grafen kan afstanden tilbagelagt af mobilen beregnes, hvilket er numerisk ækvivalent med arealet under / på kurven. På denne måde:
-Afstand tilbagelagt mellem 0 og 3 sekunder = 2 m / s. 3 s = 6 m
-Mellem 3 og 5 sekunder blev han stoppet, derfor rejste han ikke nogen afstand.
-Afstand tilbagelagt mellem 5 og 9 sekunder = 3 m / s. 4 s = 12 m
I alt rejste mobilen 18 m. Bemærk, at selvom hastigheden er negativ i intervallet mellem 5 og 9 sekunder, er den tilbagelagte afstand positiv. Hvad der sker er, at i løbet af dette tidsinterval havde mobilen ændret følelsen af sin hastighed.
Referencer
- Geogebra. Konstant funktioner. Gendannet fra: geogebra.org.
- Maplesoft. Den konstante funktion. Gendannet fra: maplesoft.com.
- Wikibooks. Beregning i en variabel / Funktioner / Konstant funktion. Gendannet fra: es.wikibooks.org.
- Wikipedia. Konstant funktion. Gendannet fra: en.wikipedia.org
- Wikipedia. Konstant funktion. Gendannet fra: es.wikipedia.org.

Endnu ingen kommentarer