
Homografisk funktion, hvordan man tegner graf, løste øvelser
Det det virkedehomografisk eller rationel ion Det er en type matematisk funktion, der består af delingen af to polynomiske komponenter. Det adlyder formularen P (x) / Q (x), hvor Q (x) ikke kan tage en null form.
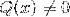
Eksempelvis svarer udtrykket (2x - 1) / (x + 3) til en homografisk funktion med P (x) = 2x - 1 og Q (x) = x + 3.

De homografiske funktioner udgør et afsnit af undersøgelsen af de analytiske funktioner, der behandles ud fra den grafiske tilgang og fra studiet af domænet og området. Dette skyldes de begrænsninger og grunde, der skal anvendes til deres opløsninger..
Artikelindeks
- 1 Hvad er en homografisk funktion?
- 2 Blandet homografisk funktion
- 2.1 Selv den niende rod af den homografiske funktion
- 2.2 Logaritme for den homografiske funktion
- 3 Sådan tegnes en homografisk funktion?
- 3.1 Rødder
- 3.2 Lodret asymptote
- 3.3 Vandret asymptote
- 3.4 Vækstinterval
- 3.5 Henfaldsinterval
- 3.6 Skæringspunkt med Y
- 4 eksempler
- 4.1 Øvelse 1
- 4.2 Øvelse 1.2
- 5 Øvelse 2
- 6 Referencer
Hvad er en homografisk funktion?
De er rationelle udtryk for en enkelt variabel, selvom dette ikke betyder, at der ikke findes et lignende udtryk for to eller flere variabler, hvor det allerede ville være i nærvær af legemer i rummet, der adlyder de samme mønstre som den homografiske funktion i flyet.
De har reelle rødder i nogle tilfælde, men eksistensen af lodrette og vandrette asymptoter opretholdes altid såvel som intervaller for vækst og fald. Almindeligvis er kun en af disse tendenser til stede, men der er udtryk, der kan vise begge dele i deres udvikling..
Dets domæne er begrænset af nævnernes rødder, da der ikke er nogen division med nul af de reelle tal.
Blandet homografisk funktion
De er meget hyppige i beregningen, især differentieret og integreret, og er nødvendige for at udlede og antidive under bestemte formler. Nogle af de mest almindelige er klassificeret nedenfor.
Selv nth rod af den homografiske funktion
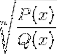
Ekskluder alle elementer fra domænet, der gør argumentet negativt. Rødderne til stede i hvert polynomisk udbytteværdi på nul, når de vurderes.
Disse værdier accepteres af radikalen, selvom den grundlæggende begrænsning af den homografiske funktion skal overvejes. Hvor Q (x) ikke kan modtage nulværdier.
Intervalløsningerne skal opfanges:
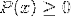
For at opnå løsningen af krydsene kan metoden til skilte blandt andet bruges.
Logaritme for den homografiske funktion
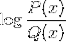
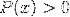
Det er også almindeligt at finde begge udtryk i et, blandt andre mulige kombinationer.
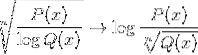
Sådan tegnes en homografisk funktion?
Homografiske funktioner svarer grafisk til hyperboler i planet. Som transporteres vandret og lodret i henhold til de værdier, der definerer polynomierne.
Der er flere elementer, som vi skal definere for at tegne en rationel eller homografisk funktion.
Ejendom
Den første vil være rødderne eller nuller til funktionerne P og Q.
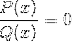
De opnåede værdier angives på grafens x-akse. Angiver krydset i grafen med aksen.
Lodret asymptote
De svarer til lodrette linjer, der afgrænser grafen i henhold til de tendenser, som disse præsenterer. De berører x-aksen ved de værdier, der gør nævneren nul og vil aldrig blive berørt af grafen for den homografiske funktion.
Vandret asymptote
Repræsenteret med en vandret stinglinje afgrænser den en grænse, for hvilken funktionen ikke vil blive defineret på det nøjagtige punkt. Trends vil blive observeret før og efter denne linje.
For at beregne det må vi ty til en metode svarende til L'Hopitals metode, der bruges til at løse grænser for rationelle funktioner, der har tendens til uendelig. Vi skal tage koefficienterne for de højeste kræfter i funktionens tæller og nævneren.
For eksempel har følgende udtryk en vandret asymptote ved y = 2/1 = 2.
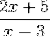
Vækstinterval
Ordinatværdierne vil have tendenser markeret på grafen på grund af asymptoter. I tilfælde af vækst stiger funktionen i værdier, når elementerne i domænet evalueres fra venstre mod højre.
Sænk interval
Ordinatværdierne falder, når domæneelementerne evalueres fra venstre til højre.
De spring, der findes i værdierne, tages ikke med i betragtning, når de stiger eller falder. Dette sker, når grafen er tæt på en lodret eller vandret asymptote, hvor værdierne kan variere fra uendelighed til negativ uendelighed og omvendt..
Y kryds
Ved at indstille værdien af x til nul finder vi skæringspunktet med ordinataksen. Dette er et meget nyttigt stykke information til opnåelse af grafen for den rationelle funktion.
Eksempler
Definer grafen for følgende udtryk, find deres rødder, lodrette og vandrette asymptoter, intervaller for vækst og fald og skæringspunkt med ordinataksen.
Øvelse 1
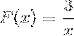
Udtrykket har ingen rødder, fordi det har en konstant værdi i tælleren. Begrænsningen til at gælde vil være x forskellig fra nul. Med vandret asymptote ved y = 0 og lodret asymptote ved x = 0. Der er ingen skæringspunkter med y-aksen.
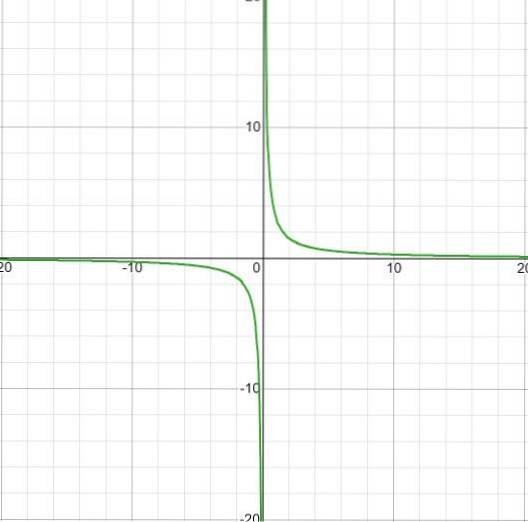
Det observeres, at der ikke er nogen vækstintervaller, selv med springet fra minus til plus uendelig ved x = 0.
Henfaldsintervallet er
ID: (-∞; o) U (0, ∞)
Øvelse 1.2
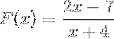
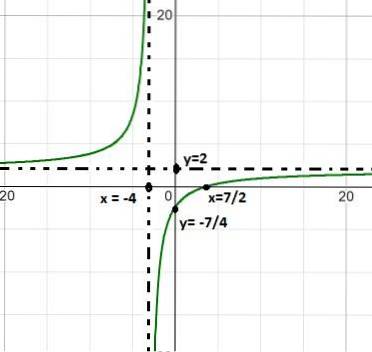
2 polynomer observeres som i den oprindelige definition, så vi fortsætter i henhold til de etablerede trin.
Den fundne rod er x = 7/2, hvilket er resultatet af at indstille funktionen lig med nul.
Den lodrette asymptote er ved x = - 4, hvilket er den værdi, der er ekskluderet fra domænet af den rationelle funktionsbetingelse.
Den vandrette asymptote er ved y = 2, dette efter opdeling af 2/1, koefficienterne for variablerne i grad 1.
Det har en y-skæring = - 7/4. Værdi fundet efter ligning med x til nul.
Funktionen vokser konstant med et spring fra plus til minus uendelig omkring roden x = -4.
Dens vækstinterval er (-∞, - 4) U (- 4, ∞).
Når værdien af x nærmer sig uendelighed, tager funktionen værdier tæt på 2. Det samme sker, når x nærmer sig mere uendelighed.
Udtrykket nærmer sig plus uendeligt, når man vurderer til - 4 fra venstre, og til minus uendelighed, når man vurderer til - 4 fra højre.
Øvelse 2
Grafen for følgende homografiske funktion observeres:
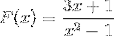
Beskriv dens opførsel, rødder, lodrette og vandrette asymptoter, vækst- og faldintervaller og skæringspunkt med ordinataksen..
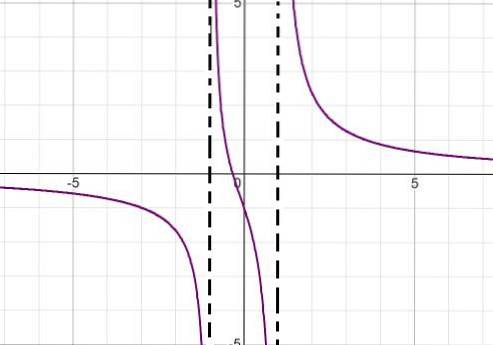
Nævneren af udtrykket fortæller os ved at faktorisere forskellen i kvadrater (x + 1) (x - 1) værdierne af rødderne. På denne måde kan begge lodrette asymptoter defineres som:
x = -1 og x = 1
Den vandrette asymptote svarer til abscissaksen, fordi den højeste effekt er i nævneren.
Dens eneste rod er defineret med x = -1/3.
Udtrykket falder altid fra venstre til højre. Det nærmer sig nul, når det nærmer sig uendeligt. Minus uendelighed, når du nærmer dig -1 fra venstre. Et plus uendeligt, når det nærmer sig -1 fra højre. Minus uendelighed når man nærmer sig 1 fra venstre og mere uendelighed når man nærmer sig 1 fra højre.
Referencer
- Tilnærmelse med rationelle funktioner. Donald J. Newman. American Mathematical Soc., 31. dec. 1979
- Ortogonale rationelle funktioner. UNIVERSIDAD DE LA LAGUNA TENERIFE ADHEMAR BULTHEEL, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njastad. Cambridge University Press, 13. feb. 1999
- Rationel tilnærmelse af reelle funktioner. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3. mar. 2011
- Algebraiske funktioner. Gilbert Ames Bliss. Courier Corporation, 1. jan 2004
- Tidsskrift for det spanske matematiske samfund, bind 5-6. Spanish Mathematical Society, Madrid 1916



Endnu ingen kommentarer