
Transcendente funktionstyper, definition, egenskaber, eksempler
Det transcendente funktioner Elementære er eksponentielle, logaritmiske, trigonometriske, inverse trigonometriske funktioner, hyperbolske og inverse hyperbolske. Det vil sige, de er dem, der ikke kan udtrykkes ved hjælp af et polynom, et kvotient af polynomer eller rødder af polynomer..
De ikke-elementære transcendente funktioner er også kendt som specielle funktioner, og blandt dem kan fejlfunktionen navngives. Det algebraiske funktioner (polynomer, kvotienter af polynomer og rødder af polynomer) sammen med transcendente funktioner elementaler udgør det, der i matematik er kendt som elementære funktioner.
Transcendente funktioner betragtes også som de, der skyldes operationer mellem transcendente funktioner eller mellem transcendente og algebraiske funktioner. Disse operationer er: summen og forskellen på funktioner, produkt og kvotient af funktioner samt sammensætningen af to eller flere funktioner.
Artikelindeks
- 1 Definition og egenskaber
- 1.1 Eksponentiel funktion
- 1.2 Egenskaber for den eksponentielle funktion
- 1.3 Logaritmisk funktion
- 1.4 Egenskaber for logaritmefunktionen
- 1.5 Funktioner til sinus, cosinus og tangent
- 2 Derivater og integraler
- 2.1 Afledt af den eksponentielle funktion
- 2.2 Integration af den eksponentielle funktion
- 2.3 Tabel over derivater og integraler af transcendente funktioner
- 3 eksempler
- 3.1 Eksempel 1
- 3.2 Eksempel 2
- 4 Referencer
Definition og egenskaber
Eksponentiel funktion
Det er en reel funktion af den virkelige uafhængige variabel i formen:
f (x) = a ^ x = ax
hvor til er et positivt reelt tal (a> 0) fast kaldes basen. Circflex eller overskrift bruges til at betegne den forstærkende operation.
Lad os sige a = 2 så ser funktionen sådan ud:
f (x) = 2 ^ x = 2x
Hvilket vil blive evalueret for flere værdier af den uafhængige variabel x:

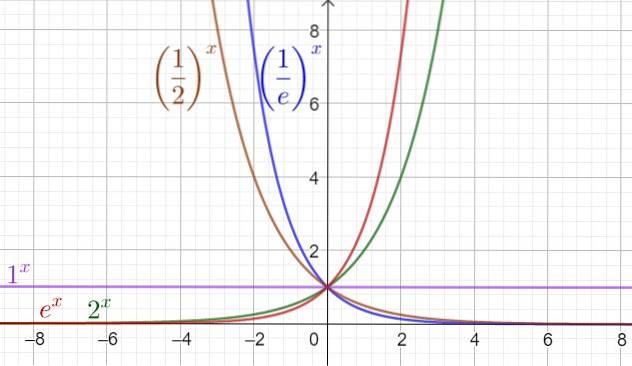
Nedenfor er en graf, hvor den eksponentielle funktion er repræsenteret for forskellige værdier af basen, inklusive basen og (Neper nummer og ≃ 2,72). Grundlag og er så vigtigt, at når vi taler om en eksponentiel funktion, tænker vi generelt e ^ x, hvilket også er betegnet exp (x).

Egenskaber for den eksponentielle funktion
Fra figur 1 kan det ses, at domænet for eksponentielle funktioner er de reelle tal (Dom f = R) og området eller stien er de positive realer (Ran f = R+).
På den anden side, uanset værdien af basen a, passerer alle eksponentielle funktioner gennem punktet (0, 1) og gennem punktet (1, a).
Når basen a> 1, så stiger funktionen og hvornår 0 < a < 1 funktionen er faldende.
Kurver på y = a ^ x og af y = (1 / a) ^ x er symmetriske omkring aksen Y.
Bortset fra sagen a = 1, den eksponentielle funktion er injektiv, det vil sige at hver værdi af billedet svarer til en og kun en startværdi.
Logaritmisk funktion
Det er en reel funktion af reel uafhængig variabel baseret på definitionen af logaritmen for et tal. Logaritmen, der skal baseres til af et nummer x, Det er antallet Y som basen skal hæves for at opnå argumentet x:
logtil(x) = y ⇔ a ^ y = x
Det vil sige logaritmefunktion i basen til er den omvendte funktion af den eksponentielle funktion i basen til.
For eksempel:
logto1 = 0, da 2 ^ 0 = 1
En anden sag, logto4 = 2, fordi 2 ^ 2 = 4
Logaritmen til roden til 2 er logto√2 = ½, fordi 2 ^ ½ = √2
logto ¼ = -2, da 2 ^ (- 2) = ¼
Nedenfor er en graf over logaritmefunktionen i forskellige baser.
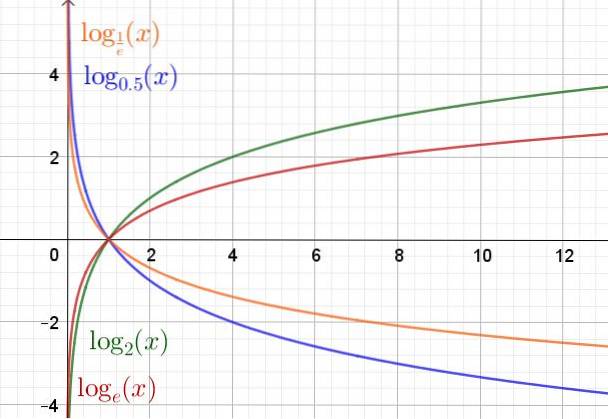
Egenskaber for logaritmefunktionen
Domænet for logaritmefunktionen y (x) = logtil(x) er de positive reelle tal R+. Området eller området er de reelle tal R.
Uanset basis passerer logaritmefunktionen altid gennem punktet (1,0), og punktet (a, 1) hører til grafen for denne funktion.
I tilfælde af at basen a er større end enhed (a> 1) stiger logaritmefunktionen. Men hvis (0 < a < 1) entonces es una función decreciente.
Sinus-, Cosine- og Tangent-funktioner
Sinusfunktionen tildeler et reelt tal y til hver x-værdi, hvor x repræsenterer målingen af en vinkel i radianer. For at opnå værdien af Sen (x) for en vinkel er vinklen repræsenteret i enhedscirklen, og projektionen af nævnte vinkel på den lodrette akse er sinus svarende til den vinkel.
Det følgende viser (i figur 3) den trigonometriske cirkel og sinus for forskellige vinkelværdier X1, X2, X3 og X4.
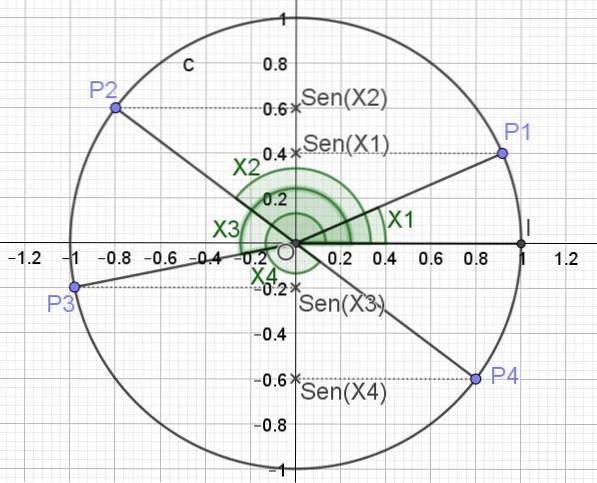
Defineret på denne måde er den maksimale værdi, som funktionen Sen (x) kan have, 1, der opstår, når x = π / 2 + 2π n, hvor n er et heltal (0, ± 1, ± 2,). Den mindste værdi, som funktionen Sen (x) kan tage, opstår, når x = 3π / 2 + 2π n.
Cosinusfunktionen y = Cos (x) er defineret på en lignende måde, men projiceringen af vinkelpositionerne P1, P2 osv. Udføres på den vandrette akse i den trigonometriske cirkel..
På den anden side er funktionen y = Tan (x) kvotienten mellem sinusfunktionen og cosinusfunktionen.
Nedenfor er en graf over de transcendente funktioner Sen (x), Cos (x) og Tan (x)
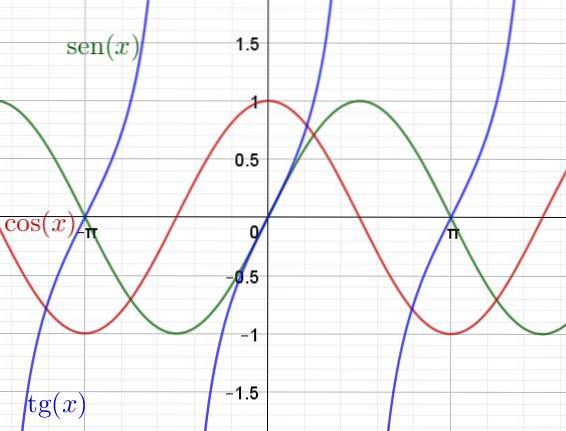
Derivater og integraler
Afledt af den eksponentielle funktion
Afledte Y ' af den eksponentielle funktion y = a ^ x er funktionen a ^ x ganget med naturlig logaritme af base a:
y '= (a ^ x)' = a ^ x ln a
I det særlige tilfælde af basen og, afledningen af den eksponentielle funktion er selve den eksponentielle funktion.
Integreret af den eksponentielle funktion
Den ubestemte integral af a ^ x er selve funktionen divideret med basens naturlige logaritme.
I det særlige tilfælde af basen e er integrationen af den eksponentielle funktion selve den eksponentielle funktion.
Tabel over derivater og integraler af transcendente funktioner
Nedenfor er en oversigtstabel over de vigtigste transcendente funktioner, deres derivater og ubestemte integraler (antiderivativer):

Eksempler
Eksempel 1
Find den funktion, der er resultatet af sammensætningen af funktionen f (x) = x ^ 3 med funktionen g (x) = cos (x):
(f eller g) (x) = f (g (x)) = cos3(x)
Dens derivat og dets ubestemte integral er:
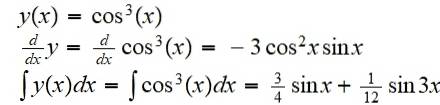
Eksempel 2
Find sammensætningen af funktionen g med funktionen f, hvor g og f er funktionerne defineret i det foregående eksempel:
(g eller f) (x) = g (f (x)) = cos (x3)
Det skal bemærkes, at sammensætningen af funktioner ikke er en kommutativ operation.
Den afledte og den ubestemte integral for denne funktion er henholdsvis:

Integralet blev efterladt angivet, fordi det ikke er muligt at skrive resultatet som en kombination af elementære funktioner nøjagtigt.
Referencer
- Beregning af en enkelt variabel. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. nov 2008
- The Implicit Function Theorem: History, Theory, and Applications. Steven G. Krantz, Harold R. Parks. Springer Science & Business Media, 9. nov. 2012
- Multivariabel analyse. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. dec. 2010
- Systemdynamik: Modellering, simulering og kontrol af mekatroniske systemer. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. mar 2012
- Calculus: Matematik og modellering. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. jan 1999
- wikipedia. Transcendent funktion. Gendannet fra: es.wikipedia.com

Endnu ingen kommentarer