
Grundlæggende trigonometriske funktioner i det kartesiske plan, eksempler, øvelse
Det trigonometriske funktioner af ægte variabel svarer til en hvilken som helst vinkel (udtrykt i radianer), et trigonometrisk forhold, som kan være sinus, cosinus, tangens, cotangent, secant og cosecant.
På denne måde har vi de seks trigonometriske funktioner: sinus, cosinus, tangens, cosecant, secant og cotangent..
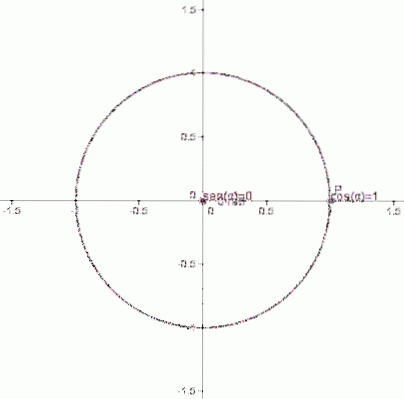
De trigonometriske funktioner for vinkler mellem 0 og 2π defineres ved hjælp af enhedscirklen, med radius 1, og hvis centrum falder sammen med oprindelsen til det kartesiske koordinatsystem: punktet (0,0).
Vi kan finde ethvert punkt P med koordinater (x, y) på denne omkreds.
Det segment, der forbinder oprindelsen med P, sammen med de respektive segmenter, der forbinder projektionerne af P på koordinatakserne, udgør en højre trekant, hvis trigonometriske forhold er kendt som forholdet mellem siderne af trekanten. A) Ja:
- sin θ = modsat ben / hypotenus
- cos θ = tilstødende ben / hypotenus
- tg θ = modsat ben / tilstødende ben
Og nu er årsagerne, der er omvendte af de foregående:
- sek θ = hypotenus / tilstødende ben
- cosec θ = hypotenus / modsat ben
- ctg θ = tilstødende ben / modsatte ben
I enhedscirklen er hypotenusen i en hvilken som helst trekant lig med 1, og benene er værd x og y, så:
sin θ = y
cos θ = x
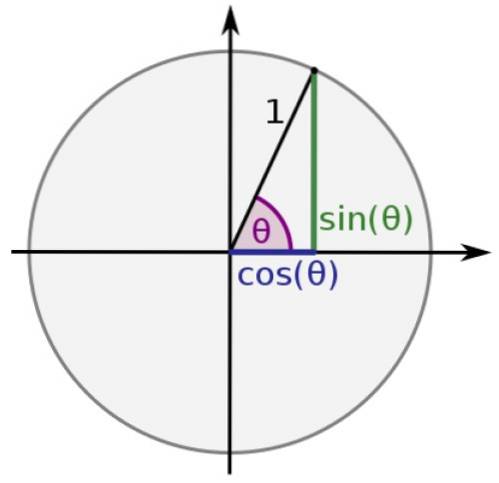
På denne måde får sinus- og cosinusfunktionerne altid værdier mellem -1 og 1, mens resten:
tg θ = y / x
cosec θ = 1 / y
sek θ = 1 / x
De defineres ikke hvornår x eller Y værd 0.
Artikelindeks
- 1 Trigonometriske funktioner i det kartesiske plan
- 1.1 Funktion f (x) = sin x
- 1.2 Funktion f (x) = cos x
- 1.3 Diskontinuerlige trigonometriske funktioner
- 2 Øvelse løst
- 2.1 Løsning
- 3 Referencer
Trigonometriske funktioner på det kartesiske plan
Som vi vil se nedenfor, er trigonometriske funktioner karakteriseret ved at være periodiske. Derfor er de ikke bindende, undtagen i et begrænset domæne..
Funktion f (x) = sin x
Startende på den trigonometriske cirkel ved punkt P (1,0) er vinklen 0 radianer. Derefter roterer radius mod uret, og sin x-funktionen vokser gradvist, indtil den når π / 2 radianer (90º), svarende til ca. 1.571 radianer..
Der når den værdien y = 1 og falder derefter, indtil den når nul i π radianer (180 °). Senere falder det endnu mere, da værdien bliver negativ, indtil den når -1, når vinklen er 3π / 2 radianer (270 °).
Endelig øges den igen, indtil den vender tilbage til nul i 360 °, hvor alt begynder igen. Dette gør y = sin x a periodisk funktion i periode 2π, derfor er sinusfunktionen ikke bijektiv.
Grafen er også symmetrisk i forhold til punktet (0,0), derfor er funktionen ulige.
Derefter er grafen for y = sin x:
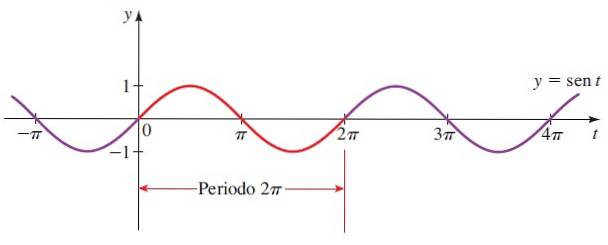
Sektionen med rødt er den første periode. Negative vinkler overvejes også, da trigonometrisk cirkels radius kan rotere med uret.
Sin domæne x = Alle virkelige.
Syndens rækkevidde eller sti x = [-1,1]
Funktion f (x) = cos x
Ved punktet P (1,0) er cosinus-funktionen 1 værd, og derfra falder den og når 0, når vinklen er π / 2. Det fortsætter med at falde og tager negative værdier, indtil det når -1 i vinklen π.
Derefter begynder det gradvist at stige, indtil det når 0 i 3π / 2 og vender tilbage til værdien 1, når radiusen har foretaget en fuldstændig omdrejning. Derfra gentager cyklussen sig, da cos x er periodisk og også er jævn (symmetrisk omkring den lodrette akse).
Formen af cosinusfunktionen er den samme som sinusfunktionen, bortset fra at de forskydes π / 2 i forhold til hinanden..
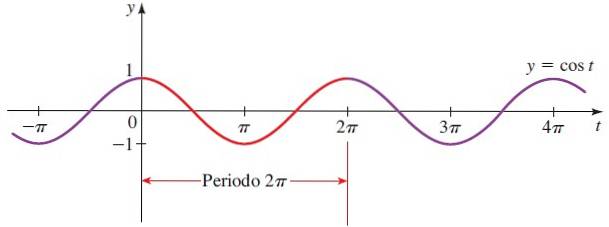
Domæne for cos x = Alle virkelige.
Cos x rækkevidde eller rejse = [-1,1]
Diskontinuerlige trigonometriske funktioner
Funktionerne tg x, ctg x, sec x og cosec x er diskontinuerlige, da de er kvotienter mellem sinus og cosinus eller det omvendte. Da disse er værd at være 0 i nogle vinkler, gør de funktionen diskontinuerlig, når de vises i nævneren.
Og da sinus og cosinus er periodiske funktioner, er funktionerne tg x, ctg x, sec x, cosec x også periodiske..
Tangentfunktion f (x) = tg x
For tangentfunktionen er diskontinuitetsværdierne: ± π / 2, ± 3π / 2, ± 5π / 2… Der tager funktionen meget store eller meget små værdier. Generelt sker dette for alle multipla af π af formen (2n + 1) π / 2, både positive og negative, med n = 0, 1, 2 ...
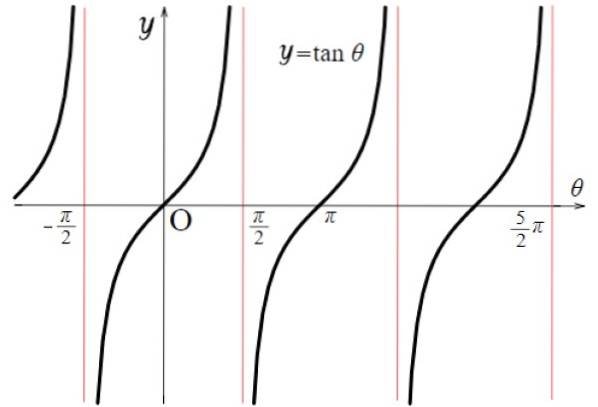
Derfor:
Tg x domæne: D = x ∈ R / x ≠ (2n + 1) π / 2; n ∈ Z
Tg x rækkevidde eller rejse: Alt rigtigt.
Bemærk, at funktionen f (x) = tg x gentages mellem - π / 2 og + π / 2, derfor er dens periode π. Derudover er det symmetrisk med hensyn til oprindelsen.
Cotangent-funktion f (x) = ctg x
For denne funktion forekommer diskontinuitetsværdierne ved 0, ± π, ± 2π…, det vil sige heltalsmultiplerne af π.
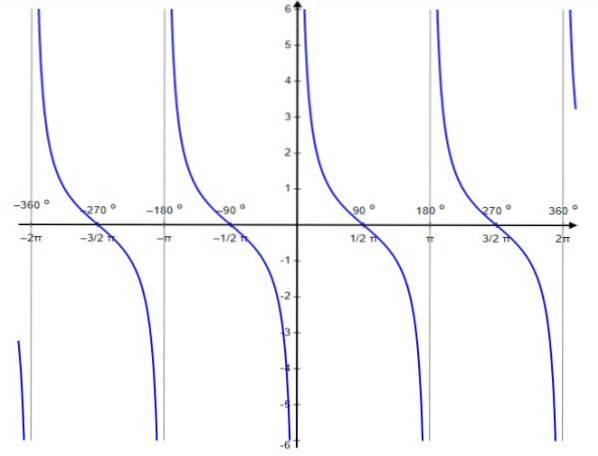
Ligesom tangentfunktionen er cotangentfunktionen periodisk af perioden π. For hende er det rigtigt, at:
Ctg x domæne: D = x ∈ R / x ≠ n π; n ∈ Z
Ctg x rækkevidde eller rejse: Alt rigtigt.
Sekantfunktion f (x) = sek x
Sec x-funktionen har diskontinuitetspunkter ved ± π / 2, ± 3π / 2, ± 5π / 2…, hvor cos x = 0. Det er også periodisk med periode π, og det observeres også fra grafen, at funktionen aldrig tager værdier i intervallet (-1,1)
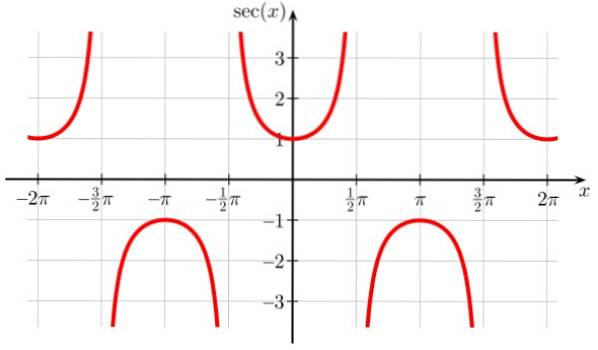
Domæne i sek x: D = x ∈ R / x ≠ (2n + 1) π / 2; n ∈ Z
Sek x rækkevidde eller rejse: Alle reelle undtagen (-1,1)
Cosecant-funktion f (x) = cosec x
Det svarer til sekantfunktionen, skønt den forskydes til højre, derfor er diskontinuitetspunkterne 0, ± π, ± 2π og alle heltalmultipler af π. Det er også periodisk.
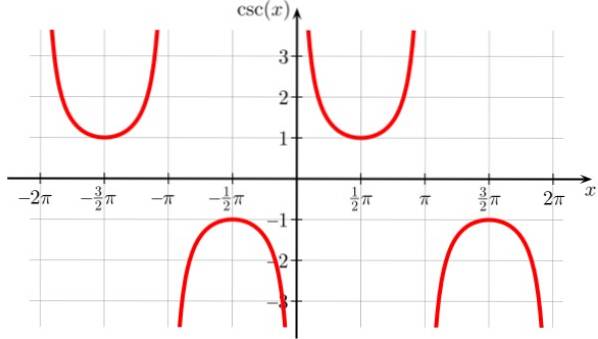
Cosec Domain X: D = x ∈ R / x ≠ n π; n ∈ Z
Høstområde eller sti x: Alle reelle undtagen (-1,1)
Træning løst
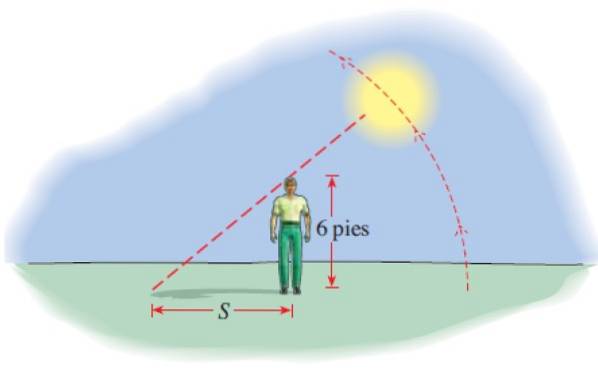
En 6 fod høj mand kaster en skygge S, hvis længde er givet af:
S (t) = 6 │seng (π.t / 12) │
Med S i fødder og t antallet af timer siden 6 AM. Hvor høj er skyggen kl.8.00, 12.00, 14.00 og 17.45?
Opløsning
Vi skal evaluere funktionen for hver af de givne værdier, bemærke, at den skal tage den absolutte værdi, da længden af skyggen er positiv:
-Kl. 8 er der gået to timer fra kl. 6, derfor er t = 2 og S (t):
S (2) = 6 │ barneseng (π.2 / 12) │ft = 6 │ barneseng (π / 6) │ft = 10,39 fod.
-Når det er 12 N, er der gået t = 6 timer, derfor:
S (6) = 6 │ barneseng (π.6 / 12) │ft = 6 │ barneseng (π / 2) │ft = 0 fod. (På det tidspunkt falder solen lodret på personens hoved).
-Kl. 14 t = 8 timer gået:
S (8) = 6 │ barneseng (π.8 / 12) │ft = 6 │ barneseng (2π / 3) │ft = 3,46 fod.
-Når klokken er 17.45, er der allerede gået 11,75 timer siden kl. 6, så:
S (11,75) = 6 │ barneseng (π x 11,75 / 12) │ fødder = 91,54 fod. På dette tidspunkt bliver skyggerne længere.
Kan læseren beregne det tidspunkt, hvor personens skygge svarer til hans højde??
Referencer
- Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
- Figuera, J. 1999. Matematik. 1. Diversificeret. Bolivarian Collegiate Editions.
- Hoffman, J. Selection of Mathematics Topics. Bind 4.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Zill, D. 1984. Algebra og trigonometri. Mcgraw bakke.


Endnu ingen kommentarer