Grader af frihed, hvordan man beregner dem, typer, eksempler

Det grader af frihed i statistik er de antallet af uafhængige komponenter i en tilfældig vektor. Hvis vektoren har n komponenter, og der er s lineære ligninger, der relaterer deres komponenter, så grad af frihed er n-p.

Begrebet grader af frihed Det vises også i teoretisk mekanik, hvor de stort set svarer til dimensionen af ​​rummet, hvor partiklen bevæger sig minus antallet af bindinger..

Denne artikel vil diskutere begrebet frihedsgrader anvendt på statistik, men et mekanisk eksempel er lettere at visualisere i geometrisk form.

Artikelindeks

• 1 Typer af frihedsgrader
  • 1.1 I et mekanisk tilfælde
  • 1.2 I et sæt tilfældige værdier
• 2 Eksempler
  • 2.1 Variation og frihedsgrader
  • 2.2 I Chi-kvadratfordelingen
  • 2.3 I hypotesetest (med eksempel udarbejdet)
• 3 Referencer

Typer af frihedsgrader

Afhængigt af den sammenhæng, hvori det anvendes, kan måden at beregne antallet af frihedsgrader variere på, men den underliggende idé er altid den samme: samlede dimensioner minus antal begrænsninger.

I et mekanisk tilfælde

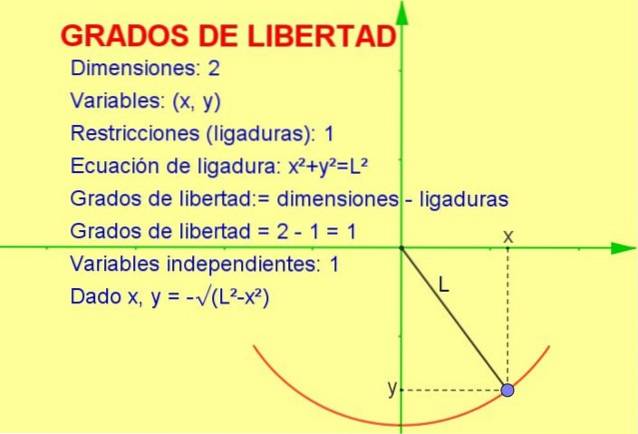
Lad os overveje en oscillerende partikel bundet til en streng (et pendul), der bevæger sig i det lodrette x-y-plan (2 dimensioner). Imidlertid er partiklen tvunget til at bevæge sig på radiusens omkreds lig med akkordlængden.

Da partiklen kun kan bevæge sig på denne kurve, er antallet af grader af frihed er 1. Dette kan ses i figur 1.

Måden at beregne antallet af frihedsgrader på er at tage forskellen i antallet af dimensioner minus antallet af begrænsninger:

frihedsgrader: = 2 (dimensioner) - 1 (ligatur) = 1

En anden forklaring, der giver os mulighed for at nå frem til resultatet, er følgende:

-Vi ved, at positionen i to dimensioner er repræsenteret af et punkt med koordinater (x, y).

-Men da punktet skal tilfredsstille ligningen af ​​omkredsen (x^to + Y^to = L^to) for en given værdi af variablen x bestemmes variablen y af ligningen eller begrænsningen.

Således er kun en af ​​variablerne uafhængige, og systemet har en (1) grad af frihed.

I et sæt tilfældige værdier

Antag vektoren for at illustrere, hvad begrebet betyder

x = (x₁, x_to,..., x_n)

Hvad repræsenterer prøven af n normalt distribuerede tilfældige værdier. I dette tilfælde den tilfældige vektor x har n uafhængige komponenter og derfor siges det at x har n grader af frihed.

Lad os nu bygge vektoren r affald

r = (x₁ - , x_to - ,…., X_n - )

Hvor repræsenterer prøve middelværdien, der beregnes som følger:

= (x₁ + x_to +…. + X_n) / n

Så summen

(x₁ - ) + (x_to - ) +…. + (X_n - ) = (x₁ + x_to +... + X_n) - n= 0

Det er en ligning, der repræsenterer en begrænsning (eller binding) på elementerne i vektoren r af resterne, da hvis n-1-komponenter i vektoren er kendt r, begrænsningsligningen bestemmer den ukendte komponent.

Derfor vektoren r af dimension n med begrænsningen:

∑ (x_jeg - ) = 0

Har (n - 1) frihedsgrader.

Igen anvendes det, at beregningen af ​​antallet af frihedsgrader er:

frihedsgrader: = n (dimensioner) - 1 (begrænsninger) = n-1

Eksempler

Variation og frihedsgrader

Variansen s^to er defineret som gennemsnittet af kvadratet af afvigelser (eller rester) af stikprøven af ​​n-data:

s^to = (r•r) / (n-1)

hvor r er vektoren for resterne r = (x1 - , x2 - ,…., Xn - ) og det tykke punkt (•) er den skalære produktoperatør. Alternativt kan variansformlen skrives som følger:

s^to = ∑ (x_jeg - )^to / (n-1)

Under alle omstændigheder skal det bemærkes, at når man beregner middelværdien af ​​residualernes kvadrat, divideres det med (n-1) og ikke med n, da som beskrevet i det foregående afsnit, antallet af frihedsgrader for vektor r er (n-1).

Hvis til beregningen af ​​variansen blev divideret med n i stedet for (n-1) ville resultatet have en bias, der er meget signifikant for værdier på n under 50 år.

I litteraturen vises variansformlen også med divisoren n i stedet for (n-1), når det kommer til variationen i en population.

Men sættet med den tilfældige variabel for restprodukterne, repræsenteret af vektoren r, Selvom den har dimension n, har den kun (n-1) frihedsgrader. Men hvis antallet af data er stort nok (n> 500), konvergerer begge formler til det samme resultat.

Regnemaskiner og regneark giver begge versioner af variansen og standardafvigelsen (som er kvadratroden af ​​variansen).

Vores anbefaling i betragtning af den analyse, der præsenteres her, er at altid vælge versionen med (n-1) hver gang det er nødvendigt at beregne variansen eller standardafvigelsen for at undgå partiske resultater..

I Chi-kvadratfordelingen

Nogle sandsynlighedsfordelinger i kontinuerlig tilfældig variabel afhænger af en kaldet parameter grad af frihed, er tilfældet med Chi-kvadratfordelingen (χ^to).

Navnet på denne parameter kommer nøjagtigt fra frihedsgraderne for den underliggende tilfældige vektor, som denne fordeling gælder for.

Antag, at vi har g-populationer, hvorfra der tages prøver af størrelse n:

x₁ = (x1₁, x1_to,… X1_n)

X2 = (x2₁, x2_to,... X2_n)

... .

x_j = (xj₁, xj_to,... Xj_n)

... .

Xg = (xg₁, xg_to,... Xg_n)

En befolkning j hvad har gennemsnit og standardafvigelse Sj, følger normalfordelingen N (, Sj ).

Den standardiserede eller normaliserede variabel zj_jeg er defineret som:

zj_jeg = (xj_jeg - ) / Sj.

Og vektoren Zj er defineret således:

Zj = (zj₁, zj_to,..., zj_jeg,..., zj_n) og følger den standardiserede normalfordeling N (0,1).

Så variablen:

Spørgsmål = ((z1₁ ^ 2 + z2₁^ 2 +…. + zg₁^ 2),…., (Z1_n^ 2 + z2_n^ 2 +…. + zg_n^ 2))

følg fordelingen χ^to(g) kaldte chi kvadratfordeling med grad af frihed g.

I hypotesetesten (med eksempel udarbejdet)

Når du vil teste hypoteser baseret på et bestemt sæt tilfældige data, skal du kende antal frihedsgrader g for at kunne anvende Chi kvadrat testen.

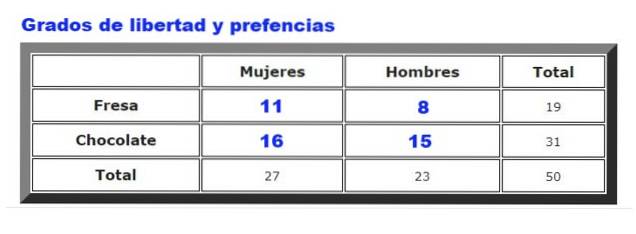
Som et eksempel analyseres de data, der er indsamlet om præferencer for chokolade eller jordbæris blandt mænd og kvinder i en bestemt isbar. Hyppigheden, hvormed mænd og kvinder vælger jordbær eller chokolade, er opsummeret i figur 2.

For det første beregnes tabellen over forventede frekvenser, som udarbejdes ved at multiplicere samlede rækker For ham samlede kolonner, divideret med samlede data. Resultatet er vist i følgende figur:

Derefter fortsætter vi med at beregne Chi-firkanten (ud fra dataene) ved hjælp af følgende formel:

χ^to = ∑ (F._eller - F_og)^to / F_og

Hvor F_eller er de observerede frekvenser (figur 2) og F_og er de forventede frekvenser (figur 3). Summationen går over alle rækker og kolonner, som i vores eksempel giver fire termer.

Efter at have udført operationerne får du:

χ^to = 0,2043.

Nu er det nødvendigt at sammenligne med den teoretiske Chi-firkant, som afhænger af antal frihedsgrader g.

I vores tilfælde bestemmes dette antal som følger:

g = (# rækker - 1) (# kolonner - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Det viser sig, at antallet af frihedsgrader g i dette eksempel er 1.

Hvis du vil kontrollere eller afvise nulhypotesen (H0: der er ingen sammenhæng mellem TASTE og KØN) med et signifikansniveau på 1%, beregnes den teoretiske Chi-kvadratværdi med frihedsgraden g = 1.

Værdien søges, der gør den akkumulerede frekvens (1 - 0.01) = 0.99, det vil sige 99%. Denne værdi (som kan opnås fra tabellerne) er 6.636.

Da den teoretiske Chi overstiger den beregnede, bekræftes nulhypotesen.

Det vil sige med de indsamlede data, Ikke observeret forholdet mellem variablerne TASTE og Køn.

Referencer

1. Minitab. Hvad er frihedsgraderne? Gendannet fra: support.minitab.com.
2. Moore, David. (2009) Grundlæggende anvendt statistik. Antoni Bosch redaktør.
3. Leigh, Jennifer. Sådan beregnes frihedsgrader i statistiske modeller. Gendannet fra: geniolandia.com
4. Wikipedia. Grad af frihed (statistik). Gendannet fra: es.wikipedia.com
5. Wikipedia. Grad af frihed (fysisk). Gendannet fra: es.wikipedia.com