Trigonometriske identiteter (eksempler og øvelser)

Det trigonometriske identiteter er forhold mellem trigonometriske forhold, som gælder for enhver værdi af variablen. For eksempel:

tan θ = sin θ / cos θ

Det er en trigonometrisk identitet, der relaterer til tre forhold mellem vinklen θ, tangenten, sinus og cosinus i nævnte vinkel.

Denne identitet gælder for alle værdier, undtagen dem, der gør 0 nævneren. Cos θ er 0 for θ = ± π / 2, ± 3π / 2, ± 5π / 2 ... Et andet eksempel på trigonometrisk identitet er:

synd x. sek x. ctg x = 1

Artikelindeks

• 1 demo
• 2 Typer af trigonometriske identiteter
  • 2.1 - Grundlæggende trigonometriske identiteter
  • 2.2 - Pythagoras identiteter
  • 2.3 - Formler for cosinus og sinus for addition / subtraktion af vinkler
  • 2.4 - Formler til den dobbelte vinkel
  • 2.5 - Formler til halv vinkel
• 3 Løst øvelser
  • 3.1 - Øvelse 1
  • 3.2 - Øvelse 2
• 4 Referencer

Demonstration

Der er to grundlæggende måder at vise, at en trigonometrisk identitet er sand:

1- Transformere et af medlemmerne af ligestillingen til det andet gennem bekvemme algebraiske manipulationer.

2- Udvikl begge medlemmer af ligestillingen hver for sig, indtil de respektive endelige udtryk for hver enkelt er nøjagtigt de samme.

I den foreslåede identitet vil vi transformere venstre side af ligestillingen, for hvilken vi udtrykker ctg x og sec x i form af sinus og cosinus som følger:

ctg x = cos x / sin x

sek x = 1 / cos x

Vi erstatter dette udtryk på venstre side af identiteten og forenkler:

synd x. (1 / cos x). (cos x / sin x) = (sin x. cos x / cos x. sin x) = 1

Og sandhedens identitet er allerede bekræftet.

Typer af trigonometriske identiteter

Der er flere klasser af trigonometriske identiteter. Vi beskriver kort de vigtigste nedenfor:

- Grundlæggende trigonometriske identiteter

Vi skelner mellem to typer grundlæggende identiteter:

I) De, der udtrykkes gennem grundforholdet sinus, cosinus og tangens:

• sek x = 1 / cos x
• cosec x / 1 / sin x
• ctg x = 1 / tg x
• tg x = sin x / cos x
• ctg x = cos x / sin x

II) De, der stammer fra paritet. Vi ved fra dens graf, at sin x er en ulige funktion, hvilket betyder at:

sin (-x) = - sin x

For sin del er cos x en jævn funktion, derfor:

cos (-x) = cos x

Derefter:

tg (-x) = sin (-x) / cos (-x) = -sen x / cos x

Tilsvarende:

• cotg (-x) = -ctg x
• sek (-x) = sek x
• cosec (-x) = - cosec x

- Pythagoras identiteter

De fås ved anvendelse af Pythagoras sætning til højre trekant af ben a og b og hypotenus c. Lad os se:

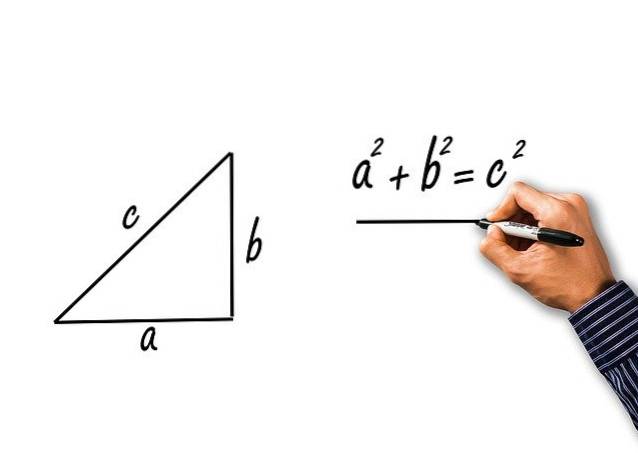
Pythagoras sætning siger, at:

c^to = a^to + b^to

Opdeler alt med c^to:

c^to / c^to = (a^to / c^to) + (B^to / c^to)

Udtrykket til venstre er 1 og husker, at sinus og cosinus i den spidse vinkel α er defineret som:

sin α = a / c

cos α = b / c

Resultat:

1 = (sin α)^to + (cos α)^to

Denne identitet er kendt som grundlæggende identitet.

Proceduren kan udføres ved at dividere med a^to og b^to, hvilket giver anledning til yderligere to identiteter:

sek^to α = 1 + tg^to a

høst^to α = 1 + ctg^to a

- Formler for cosinus og sinus for addition / subtraktion af vinkler

De vigtigste trigonometriske identiteter for cosinus, sinus og tangens for addition og subtraktion er som følger:

Bevis for synd (α + β) og cos (α + β)

Disse identiteter kan bevises geometrisk eller også ved Eulers formel:

og^ia = cos α + i sin α

Lad os se, hvad der sker med formlen, når vi erstatter summen af ​​to vinkler α og β:

og^{i (a +β)} = cos (α + β) + i sin (α + β)

Dette udtryk er komplekst, dets virkelige del er cos (α + β), og dens imaginære del er i sin (α + β). Vi gemmer dette resultat til senere brug og fokuserer på at udvikle den eksponentielle del:

og^{i (a +β)} = e^ia ⋅ e^iβ = (cos α + i sin α). (cos β + i sin β) =

= cos α⋅cos β + cos α⋅i sin β + i⋅sen α cos β - sin α⋅sen β

Den virkelige del af dette udtryk er den, der ikke ganges med den imaginære enhed "i":

cos α⋅cos β - sin α. sin β

Den imaginære del er derfor:

i (cos α⋅sen β + sin α⋅cos β)

For at to komplekse udtryk skal være ens, skal den reelle del af den ene svare til den reelle del af den anden. Det samme sker med imaginære dele.

Vi tager det gemte resultat og sammenligner det med dette:

cos α. cos β - sin α. sin β = cos (α + β)

i (cos α⋅sen β + sin α⋅cos β) = i sin (α + β)

sin (α + β) = (cos α. sin β + sin α⋅cos β)

- Formler til den dobbelte vinkel

I de foregående formler tager vi β = α og udvikler:

sin (α + α) = sin 2 α = sin α⋅cos α + cos α. sin α = 2⋅ sin α ⋅ cos α

cos (α + α) = cos 2 α = cos α⋅cos α - sin α⋅sen α = cos^to α - synd ^to a

tg (α + α) = tg 2 α = [tg α + tg α] / [1- tg α⋅tg α] = 2tg α / 1- tg^to a

Hvis vi i det andet udtryk erstatter cos^to α = 1 - synd^to α opnås:

cos 2 α = cos^to α - (1- cos^to α) = 2 cos^to a -1

- Formler til halv vinkel

I dette sidste udtryk, lad os erstatte α med α / 2, følgende forbliver:

cos α = 2 cos ^to(a / 2) -1

Løser for:

Løst øvelser

- Øvelse 1

Vis det:

Vi skal arbejde venstre sigt algebraisk, så det ligner det rigtige. Da sin x vises i det rigtige udtryk, er det første trin at udtrykke cos^tox i form af sin x, så alt er i samme trigonometriske forhold:

Derefter tages 1 - synd i betragtning^to x fordi det er en forskel på perfekte firkanter. For at gøre dette rydder det den grundlæggende identitet:

cos^tox = 1 - synd^to x

1 - sen^to x = (1- sin x) (1 + sinx)

Og faktoriseringen erstattes i det originale udtryk:

Udtrykket (1-sinx) er forenklet, og der er stadig en lighed:

1 + sin x = 1 + sinx

- Øvelse 2

Løs følgende trigonometriske ligning, og giv løsningen for værdier mellem 0 og 360º:

tg x + sek^to x = 3

Opløsning

I betegnelsen til venstre er der to trigonometriske forhold, derfor er det nødvendigt at reducere alt til en enkelt for at være i stand til at løse det ukendte. Udtrykket sek^to x udtrykkes gennem en af ​​de pythagoreiske identiteter:

sek^to α = 1 + tg^to a

Udskiftning i ligningen forbliver:

tg x + 1 + tg^to x = 3

Omarrangere vilkårene:

tg^to x + tg x + 1 = 3

Denne ligning løses ved at foretage ændringen af ​​variablen:

tg x = u

eller^to + u + 1 - 3 = 0 → u^to + u - 2 = 0

Denne kvadratiske ligning kan let løses ved factoring:

(u +2) (u-1) = 0

Derfor u₁ = -2 og u_to = 1, hvilket svarer til:

tg x₁ = -2

tg x_to = 1

Langt om længe:

x₁ = arctg (-2) = 296,6º

x_to  = arctg (1) = 45º

Referencer

1. Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
2. Figuera, J. 1999. Matematik. 1. Diversificeret. Bolivarian Collegiate Editions.
3. Hoffman, J. Selection of Mathematics Topics. Bind 4.
4. Jiménez, R. 2008. Algebra. Prentice hall.
5. Wikipedia. Trigonometri identiteter og formler. Gendannet fra: es.wikipedia.org.
6. Zapata, F. 4 måder at løse en kvadratisk ligning på. Gendannet fra: francesphysics.blogspot.com.
7. Zill, D. 1984. Algebra og trigonometri. Mcgraw bakke.