
Multiplikativ invers forklaring, eksempler, løste øvelser
Det forstås af Invers multiplikativ af et tal giver et andet tal, der ganges med det første, som resultat det neutrale element i produktet, det vil sige enheden. Hvis du har et rigtigt tal til så er dens multiplikative inverse betegnet med til-1, og det er sandt, at:
a a-1 = a-1 a = 1
Normalt antallet til tilhører et sæt reelle tal.
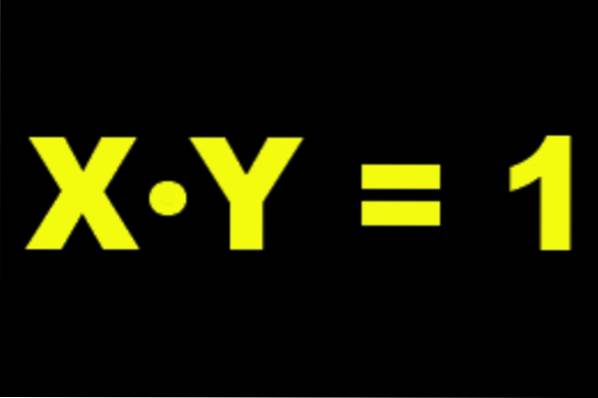
Hvis vi for eksempel tager a = 2, så er dens multiplikative inverse to-1 = ½ da følgende er bekræftet:
2 ⋅ 2-1 = 2-1⋅ 2 = 1
2⋅ ½ = ½ ⋅ 2 = 1
Til Omvendt multiplikativ af et nummer kaldes også gensidig, fordi multiplikativ invers opnås ved at udveksle tæller og nævner, for eksempel er multiplikativ invers på 3/4 4/3.
Som en generel regel kan det siges, at for et rationelt tal (p / q) dens multiplikative inverse (p / q)-1 Det er gensidigt (q / p) som kan bekræftes nedenfor:
(p / q) ⋅ (p / q)-1 = (p / q) ⋅ (q / p) = (p⋅ q) / (q⋅ p) = (p⋅ q) / (p⋅ q) = 1
Den multiplikative inverse findes ikke i det numeriske sæt af heltal, For eksempel, hvis heltal 2 tages, ville dets multiplikative inverse i henhold til hvad der er set ovenfor være ½, men a ½ er ikke et heltal..
Der er heller ingen multiplikativ invers af multiplikationens null-element. Med andre ord har tallet nul (0), som er nulelementet i multiplikationsoperationen, ikke en multiplikativ invers, da der ikke er noget tal, der multipliceres med enhed nul.
Den multiplikative inverse findes i rationelle tal, i reelle tal og i komplekse tal.
Eksempler på multiplikativ invers
Eksempel 1
Find det multiplikative inverse af 3/2, og kontroller, at det opfylder egenskaben af multiplikative heltal.
I overensstemmelse med ovenstående regel udskiftes tælleren og nævneren på denne måde multiplikativ invers af (3/2) er (2/3). For at kontrollere multiplikationen af de to tal udføres:
(3/2) ⋅ (2/3) = (3 ⋅ 2) / (2 ⋅ 3) = 6/6 = 1.
For at multiplicere to brøktal skal du blot gange tælleren for den første med tælleren for den anden for at få tælleren af resultatet..
For at opnå nævneren for et produkt med brøktal skal du fortsætte på en lignende måde, dvs. multiplicere nævnere med hinanden, og resultatet er nævneren for produktet. I vores eksempel er det verificeret, at tælleren af nummeret på produktet og dets gensidige er 6, og nævneren er 6, hvilket efterlader fraktionen 6/6, som er 1.
Eksempel 2
Den multiplikative inverse af -5 bør ikke forveksles med dens symmetriske (+5), som undertiden kaldes den aritmetiske inverse. Den multiplikative inverse opnås som følger:
(-5) ⋅ X = 1
Hvor X er den multiplikative inverse, der skal opnås. En mulig procedure er at løse det ukendte X. Da (-5) multiplicerer det ukendte X i det venstre medlem, så sker det ved at dividere det rigtige medlem:
X = 1 / (-5)
Da det er kendt, at + mellem - er -, opnås endelig X:
X = - ⅕ .
Afslutningsvis - ⅕ er den multiplikative inverse af -5.
Eksempel 3
Få multiplikativ invers af -√2. Antag, at den multiplikative inverse er X, så -√2 ganget med X skal være enhed, en betingelse, som vi stiller nedenfor:
-√2 ⋅ X = 1
Derefter divideres begge medlemmer med -√2 for at opnå:
(-√2 ⋅ X) / (-√2) = 1 / (-√2)
I det første medlem er -√2 forenklet og efterlader:
X = 1 / (-√2)
Dette udtryk kan rationaliseres, dvs. eliminere nævnens rod, multiplicere i tælleren med (-√2) og i nævneren med samme mængde, så resultatet ikke ændres:
X = (-√2) / [(-√2) (- √2)] = - (√2 / 2)
Afslutningsvis - (√2 / 2) er den multiplikative inverse af (-√2).
Eksempel 4
Antag ethvert tal x, få dets multiplikative inverse og repræsentere det grafisk.
I dette tilfælde er det en funktion f (x) = x, at opnå multiplikativ invers er at finde funktionen g (x) sådan, at ganget med enhedens første tal. Funktionen g er den gensidige af f og bør ikke på nogen måde forveksles med dens inverse funktion.
Med andre ord er den multiplikative inverse af x en y, således at følgende er sandt:
x ⋅ y = 1
hvorfra clearing og du har:
y = 1 / x.
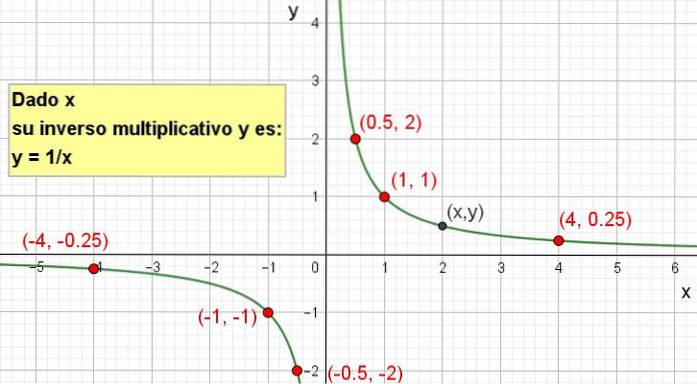
Ovenstående fortolkes således givet en værdi på x, den foregående formel giver os dens multiplikative inverse.
Det er muligt at fremstille den grafiske repræsentation som vist i følgende figur:
Uddannelse
Øvelse 1
Givet x = 2 - √2, få dets multiplikative inverse y.
Opløsning:
For at y er en multiplikativ invers af x, skal følgende ligestilling være opfyldt:
x ⋅ y = 1
Erstat x med dens værdi:
(2 - √2) ⋅ y = 1
Så rydder det og:
y = 1 / (2 - √2)
For at rationalisere resultatet ganges tælleren og nævneren med deres konjugerede binomiale:
y = (2 + √2) / ((2 + √2) (2 - √2))
I nævneren genkendes et bemærkelsesværdigt produkt kaldet produktet af en sum og en forskel, hvilket er forskellen mellem kvadraterne. På denne måde forsvinder roden i nævneren.
y = (2 + √2) / (2 ^ 2 - (√2) ^ 2)
Løsning af kræfterne:
y = (2 + √2) / (4 - 2)
Forenkling:
y = (2 + √2) / 2
Øvelse 2
Få multiplikativ invers af (1 / a + 1 / b), hvor a og b ikke er nul reelle tal.
Opløsning:
Vi kalder Y multiplikativ invers af (1 / a + 1 / b), så følgende ligning skal være opfyldt:
Og ⋅ (1 / a + 1 / b) = 1
Variablen Y ryddes:
Y = 1 / (1 / a + 1 / b)
Nævneren er løst:
Y = 1 / ((b + a) / a b)
Som det er kendt fra algebra reglerne, overgår nævneren til tælleren:
Y = (a b) / (b + a)
Det beordres til endelig at opnå:
(a b) / (a + b), som er multiplikativ invers af (1 / a + 1 / b).
Øvelse 3
Få multiplikativ invers af (a - b) / (a ^ 2 - b ^ 2).
Opløsning:
Husk, at den multiplikative inverse også kaldes den gensidige, fordi den opnås nøjagtigt ved at udveksle tæller og nævneren.
Derefter vil den multiplikative inverse af (a - b) / (a ^ 2 - b ^ 2) være:
(a ^ 2 - b ^ 2) / (a - b)
Men dette udtryk kan forenkles, hvis vi i henhold til reglerne for algebra anerkender, at tælleren er en forskel på kvadrater, der kan betragtes som et produkt af en sum ved en forskel:
((a + b) (a - b)) / (a - b)
Da der er en fælles faktor (a - b) i tælleren og nævneren, fortsætter vi med at forenkle og endelig opnår:
(a + b) som er multiplikativ invers af (a - b) / (a ^ 2 - b ^ 2).
Referencer
- Fuentes, A. (2016). GRUNDLÆGGENDE MATE. En introduktion til beregning. Lulu.com.
- Garo, M. (2014). Matematik: kvadratiske ligninger: Hvordan løser en kvadratisk ligning. Marilù Garo.
- Haeussler, E. F., & Paul, R. S. (2003). Matematik til ledelse og økonomi. Pearson Uddannelse.
- Jiménez, J., Rofríguez, M., & Estrada, R. (2005). Matematik 1 SEP. Grænseværdi.
- Preciado, C. T. (2005). Matematik kursus 3.. Redaktionel Progreso.
- Rock, N. M. (2006). Algebra I er let! Så let. Team Rock Press.
- Sullivan, J. (2006). Algebra og trigonometri. Pearson Uddannelse.



Endnu ingen kommentarer