
Hookes lovformler, eksempler, applikationer, øvelser
Det Hookes lov påpeger, at deformationen, som en elastisk genstand oplever, er direkte proportional med den kraft, der påføres den. Proportionalitetskonstanten afhænger af genstanden, dens geometri og det materiale, som den er lavet med..
Alle materialer har elastiske egenskaber i større eller mindre grad, så de overholder Hookes lov, så længe de vender tilbage til deres oprindelige dimensioner, når kraften ophører. Fjedre og elastikker er gode eksempler på genstande, der overholder Hookes lov, men det er også stålstift, der er en del af en bro.

Idet vi tager en fjeder eller fjeder som et eksempel for at holde den strakt eller komprimeret, er det nødvendigt at anvende en kraft, hvis størrelse er F. Ifølge Hookes lov vil fjederen opleve en deformation x:
F ∝ x
Konstanten af proportionalitet, som kaldes en kilde fjederstivhed konstant, betegnes som k, derfor:
F = k⋅x
I enhederne i det internationale system er kraften i newton (N) og deformationen i meter (m). Derfor har fjederkonstanten enheder på N / m. Fjederkonstanten repræsenterer den kraft, der skal påføres for at deformere den med 1 m længde.
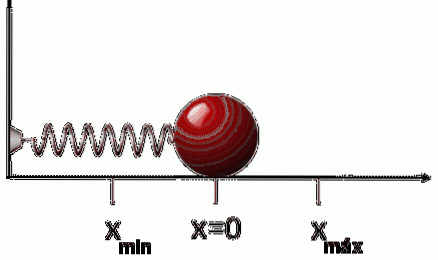
Hvis den efter strækning eller komprimering af fjederen frigøres, bevæger den sig i modsat retning af den påførte kraft. Dette betyder, at hvis vi strækker det, komprimerer det og omvendt. Derfor er kraften FR hvad foråret udøver det er:
FR = -k⋅x
Det negative tegn angiver det ovennævnte: at styrken modsætter sig forskydningen, derfor kaldes denne kraft som genoprettende kraft.
Artikelindeks
- 1 Formel og ligninger
- 1.1 Arbejde udført for at strække eller komprimere en fjeder
- 2 Eksempler på fjedre
- 2.1 Kompressionsfjeder
- 2.2 Forlængelses- og torsionsfjedre
- 2.3 Materialer til fremstilling af fjedre
- 3 Anvendelser af Hookes lov
- 4 Løst øvelser
- 4.1 - Øvelse 1
- 4.2 - Øvelse 2
- 5 Referencer
Formel og ligninger
Forholdet mellem kraft og forskydning i et forår blev opdaget af Robert Hooke (1635-1703), en bemærkelsesværdig engelsk fysiker kendt for sin rivalisering med Isaac Newton. Hooke var en alsidig videnskabsmand, der med held vovede sig ind i forskellige videnskabelige områder: mekanik, biologi, astronomi og arkitektur..

Hooke indså, at hvis kraften, der påføres en fjeder, ikke er særlig stor, deformeres fjederen proportionalt med kraften, og når denne kraft forsvinder, vender fjederen tilbage til sin naturlige længde.
Således er Hookes lov i grafisk form i form af en lige linje, hvis hældning er fjederkonstant. Det følgende billede viser den kraft, der udøves på fjederen til at strække den - eller komprimere den - som en funktion af position x. Bemærk også, at kraften ikke afhænger af fjederens naturlige længde, men af dens forskydning..
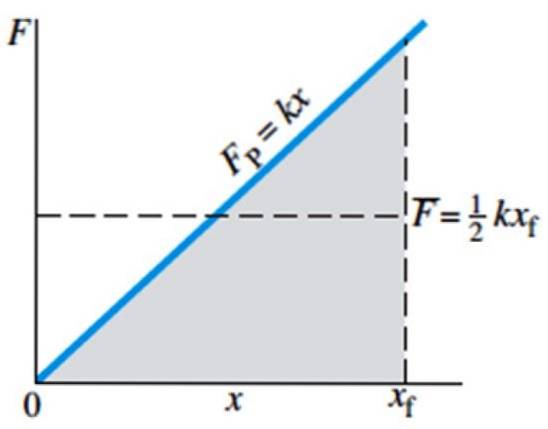
Den gennemsnitlige kraft er angivet på grafen med bjælken F og er lig med ½ kxF, hvor xF er fjederens endelige position.
Både den kraft, der udøves på fjederen, og den kraft, den udøver på en genstand, der er bundet til den, er variable kræfter. Jo mere du vil strække eller komprimere fjederen, jo mere kraft skal du anvende for at opnå det..
Arbejde udført for at strække eller komprimere en fjeder
Når en deformerende kraft påføres fjederen, udføres der arbejde, der opbevares i foråret og kan bruges senere..
Mekanisk arbejde defineres som området under grafen for kraft F som en funktion af position x. At beregne det arbejde W, som en variabel kraft F (x) gør, når en objekt flyttes fra position x1 op til position xto vi skal beregne den bestemte integral:
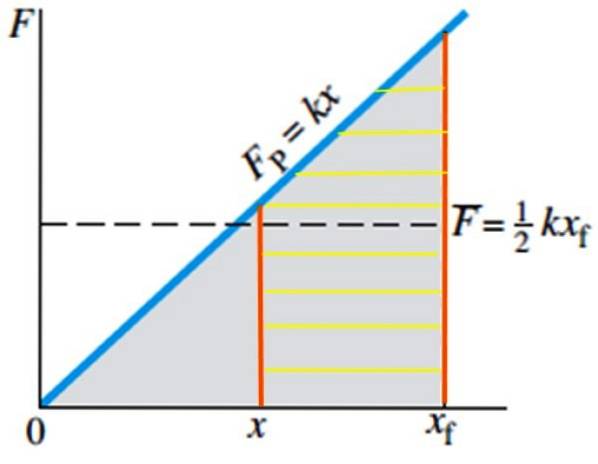
I tilfælde af det arbejde, der kræves for at bringe en fjeder fra sin ligevægtsposition til position xF Det er meget simpelt, da området, der skal beregnes, er det for den trekant, der er skygget i gråt i figur 4, hvis formel er kendt:
Areal af trekanten = ½ base. højde
Derfor er det nødvendige arbejde:
W = ½ xF . (kxF) = ½ k (xF)to
Og hvis du vil beregne det arbejde, der er nødvendigt for at bringe fjederen fra position x til position xF, svarer til at beregne arealet af den skraverede trapez i figur 5:
W = ½ k (xF)to - ½ k xto

Eksempler på fjedre
Afhængigt af den anvendelse, som de er beregnet til, kan fjedrene være spiralformede, cylindriske, koniske, spiralformede, med et cirkulært tværsnit (den mest almindelige), firkantede eller rektangulære..
En almindeligt anvendt klassificering er i henhold til den type indsats, som de vil blive udsat for: der er vridnings-, bøjnings-, kompressions- og forlængelsesfjedre. Sidstnævnte bruges i vid udstrækning, og nogle fungerer lige meget til spænding og kompression..
Kompressionsfjeder
Et eksempel på en trykfjeder er den, der bruges i legetøjet, der kaldes pogo eller springestok. Disse fjedre lagrer meget potentiel energi, når de komprimeres og frigiver den lidt efter lidt, når de vender tilbage til ligevægtspositionen. På denne måde er rebounds ikke for bratte.

Forlængelses- og torsionsfjedre
Trampolinfjedre er forlængerfjeder og er fremstillet med tæt viklede spoler med to kroge i enderne. De er i stand til at bevare en masse potentiel energi, som de derefter frigiver, når nogen klatrer op og begynder at hoppe på måtten, som også har sit eget elastiske respons, som alle materialer..
Torsionsfjedre er meget almindelige, fordi de bruges til at lave tøjnål. I stedet for kroge i enderne bøjes de i en vinkel for at modstå vridningskræfter.

Materialer til fremstilling af fjedre
De mest egnede materialer til fremstilling af fjedre er dem med en ultimativ modstand (endelig modstand) høj, det vil sige, de støtter en stor indsats, før de bryder. Det er også ønskeligt, at materialet har et højt udbyttepunkt, så det ikke mister sine elastiske kvaliteter med lille indsats..
Kraftige fjedre er lavet af legeringer inklusive kulstofstål, kobber, nikkel og bronze.
Hookes lovansøgninger
Da fjedre har dyden til at lagre potentiel energi, når de strækkes eller komprimeres, er de i stand til at udføre arbejde ved at flytte ting som mekanismer..
På denne måde har fjedrene et væld af anvendelser, lige fra små og hverdagslige genstande gennem biler til maskiner af enhver art. Fjedrene er vant til at:
-Fugt vibrationer.
-Fremstillingsmekanismer, der kan trækkes tilbage: kuglepenne, tøjnåle, hårspænder.
-Lav fjedervægte eller dynamometre
Og de er også en del af mekanismen til:
-Ure.
-Trampoliner.
-Låse.
-Legetøj.
-Våben.
-Nåelmålere, for eksempel galvanometeret, bruges til at måle strømme, spændinger og modstande.
Løst øvelser
- Øvelse 1
En kraft på 5,0 N påføres en fjeder, hvilket får en længde på 3,5 cm til at blive strakt fra sin naturlige længde..
a) Hvor meget strækker det sig, når den påførte kraft er 7 N?
b) Find det arbejde, der er udført af den påførte kraft for at strække fjederen 3,5 cm fra sin naturlige længde.
Løsning til
Når vi ved, at fjederen strækkes 3,5 cm ved at anvende 5,0 N, kan vi beregne dens konstante:
k = F / x = 5,0 N / 3,5 cm = 1,43 N / cm.
Når en kraft på 7 N påføres, opnås følgende strækning:
x = F / k = 7,0 N / 1,43 N / m = 4,9 cm
Løsning b
Arbejdet, der kræves for at deformere en fjeder, gives af:
W = ½ kxto = 0,5 x 1,43 N / cm x (3,5 cm)to = 8,76 N. cm = 8,76 N. 1 x 10 -to m = 0,0876 J.
- Øvelse 2
En fjeder med ubetydelig masse og 10 cm lang er ophængt fra en støtte. Hvis en 2 kg masse hænges på den, strækkes fjederen til 15 cm. Beregn:
a) Fjederkonstanten
b) Fjederens størrelse, når en 3 kg masse suspenderes.
Løsning til
Fjederstrækningen er x = 15 - 10 cm = 5 cm
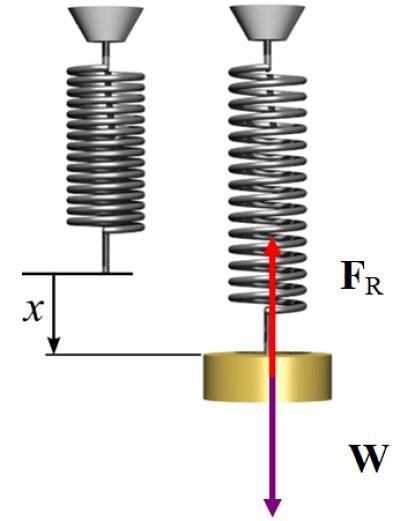
Da systemet er i statisk ligevægt, styres den kraft, som fjederen udøver, når der strækkes, lodret opad for at kompensere for vægten, som er rettet nedad, og derefter:
FR = W → kx = mg
k = 2 x 9,8 N / 5 x 10 -to m = 392 N / m
Løsning b
Når en vægt på 3 kg er suspenderet, er den nye kraft W = 3 x 9,8 N = 29,4 N
I et sådant tilfælde er strækningen:
x = mg / k = 29. 4 N / 392 N / m = 0,075 m = 7,5 cm
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill.
- Blog om kreative mekanismer. Fire forskellige fjedertyper. Gendannet fra: creativemechanisms.com.
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 2. dynamik. Redigeret af Douglas Figueroa (USB).
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed. Prentice Hall.
- .



Endnu ingen kommentarer