
Keplers love forklaring, øvelser, eksperiment
Det Keplers love på planetarisk bevægelse blev formuleret af den tyske astronom Johannes Kepler (1571-1630). Kepler udledte dem på baggrund af hans lærers arbejde den danske astronom Tycho Brahe (1546-1601).
Brahe kompilerede omhyggeligt data om planetbevægelser i mere end 20 år med overraskende præcision og nøjagtighed i betragtning af at teleskopet endnu ikke var opfundet på det tidspunkt. Gyldigheden af dine data er stadig gyldig i dag.

Artikelindeks
- 1 Keplers 3 love
- 2 Loven om universel tyngdekraft og Keplers tredje lov
- 3 Øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 eksperiment
- 4.1 Materialer
- 4.2 Fremgangsmåde
- 5 Referencer
Keplers 3 love
Keplers love siger:
-Første lov: alle planeter beskriver elliptiske kredsløb med solen i et af brændpunkterne.
-Anden lov eller lov om lige områder: en linje rettet fra solen til enhver planet (fokal radius), fejer lige områder i lige tid.
-Tredje lov: kvadratet af den tid, det tager for en planet at kredse om Solen, er proportional med terningen af dens gennemsnitlige afstand fra Solen.
Være T sagde tiden, kaldte omløbstid, Y r den gennemsnitlige afstand, derefter:
Tto er proportional med r3
T = k r3
Dette betyder, at kvotienten Tto/ r3 er den samme for alle planeter, hvilket gør det muligt at beregne kredsløbsradius, hvis kredsløbsperioden er kendt.
Hvornår T udtrykkes i år og r i astronomiske enheder AU * er proportionalitetskonstanten k = 1:
Tto= r3
* En astronomisk enhed svarer til 150 millioner kilometer, hvilket er den gennemsnitlige afstand mellem jorden og solen. Jordens kredsløb er 1 år.
Loven om universel tyngdekraft og Keplers tredje lov
Den universelle lov for tyngdekraft siger, at størrelsen af tyngdekraftens tiltrækningskraft mellem to massegenstande M Y m henholdsvis hvis centre er adskilt af en afstand r, er givet af:
F = G mM / rto
G er den universelle gravitationskonstant, og dens værdi er G = 6,674 x 10 -elleve N.mto/ kgto .
Nu er planeternes baner elliptiske med en meget lille excentricitet.
Dette betyder, at banen ikke er meget langt fra en omkreds, undtagen i nogle tilfælde som dværgplaneten Pluto. Hvis vi tilnærmer banerne til den cirkulære form, er accelerationen af planetens bevægelse:
tilc = vto/ r
På grund af F = ma, har:
G mM / rto = m.vto/ r
Her v er planetens lineære hastighed omkring Solen, antaget statisk og med masse M, mens planetens er m. Derefter:

Dette forklarer, at planeterne længere væk fra solen har en lavere omløbshastighed, da dette afhænger af 1 / √r.
Da afstanden planeten bevæger sig, er cirka længden af omkredsen: L = 2πr og det tager en tid lig med T, kredsløbets periode, opnår vi:
v = 2πr / T
Ligning af begge udtryk for v giver et gyldigt udtryk for Tto, kvadratet i omløbsperioden:

Og dette er netop Keplers tredje lov, da i dette udtryk parentes 4πto / GM er derfor konstant Tto er proportional med afstanden r kuberet.
Den endelige ligning for kredsløbsperioden opnås ved at tage kvadratroden:

Hvor meget er solens masse værd? Det er muligt at finde ud af ved denne ligning. Vi ved, at jordens kredsløbsperiode er et år, og kredsløbsradiusen er 1 AU svarende til 150 millioner kilometer, så vi har alle de nødvendige data.
I vores tidligere ligning løser vi for M, ikke uden først at konvertere alle værdier til det internationale system af enheder SI:
1 år = 3,16 x 107 sekunder.
1 AU = 150 millioner km = 1,5 x10elleve m.

Uddannelse
Selvom Kepler kun havde planeterne i tankerne, da han udledte sine berømte love, er disse også gyldige for bevægelse af satellitter og andre kroppe i solsystemet, som vi vil se nedenfor..
- Øvelse 1
Ved at vide, at Jupiters bane er 5,19 gange Jorden, finder du Jupiters omløbstid.
Opløsning
I henhold til definitionen af den astronomiske enhed er Jupiter fjernt fra solen 5.19 AU, derfor ifølge Keplers tredje lov:
Tto= r3= (5,19)3 flere år
Derfor T = (5,19)3/2 år = 11,8 år
- Øvelse 2
Komet Halley besøger solen hvert 75,3 år. Finde:
a) Den halv-store akse for dens bane.
b) Aphelion-foranstaltningen, hvis periheliet måler 0,568 AU.
Opløsning
Komet Halley besøger solen hvert 75,3 år. Finde:
a) Den halv-store akse for dens bane.
b) Aphelion-foranstaltningen, hvis periheliet måler 0,568 AU.
Løsning til
Når en planet eller en hvilken som helst anden stjerne er ved sit nærmeste punkt til solen, siges det at være i perihelion, og når det er længere væk, i aphelion. I det specielle tilfælde af en cirkulær bane er r i Keplers tredje lov baneens radius.
I den elliptiske bane er himmellegemet dog mere eller mindre langt fra solen, hvor den halv-store akse "a" er gennemsnittet mellem aphelion og perihelion:

Derfor erstatter vi r med a i Keplers tredje lov, som resulterer for Halley i:
Tto= a3→ a = (T)2/3 → a = (75,3) 2/3 UA = 17.832 UA
Løsning b
a = ½ (Perihelion + Aphelion)
17.832 = ½ (0.568+ Aphelion) → Aphelion = 2 x 17.832 - 0.568 AU = 35.10 AU.
Eksperiment
Analysering af planetenes bevægelse kræver uger, måneder og endda år med omhyggelig observation og registrering. Men i laboratoriet kan der udføres et meget simpelt skalaeksperiment for at bevise, at Keplers lov om lige områder holder..
Til dette kræves et fysisk system, hvor styrken, der styrer bevægelsen, er central, en tilstrækkelig betingelse for, at loven om områder kan opfyldes. Et sådant system består af en masse bundet til et langt reb, med den anden ende af tråden fastgjort til en støtte..
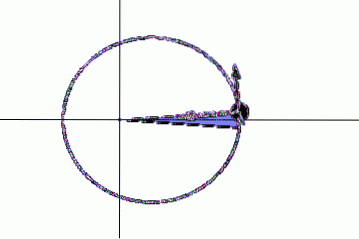
Massen bevæges en lille vinkel fra sin ligevægtsposition, og der gives en lille impuls til den, så den udfører en oval (næsten elliptisk) bevægelse i det vandrette plan, som om det var en planet omkring Solen..
På den kurve, der er beskrevet af pendulet, kan vi bevise, at den fejer lige store områder på lige tid, hvis:
-Vi overvejer vektorradier, der går fra tiltrækningscenteret (begyndelsesbalancepunkt) til massens position.
-Og vi fejer mellem to på hinanden følgende øjeblikke af samme varighed i to forskellige områder af bevægelsen.
Jo længere pendulstrengen er og jo mindre vinklen er væk fra lodret, vil nettogendannelseskraften være mere vandret, og simuleringen ligner tilfældet med bevægelse med central kraft i et plan.
Derefter nærmer den beskrevne ovale sig til en ellipse, som den, som planeterne rejser.
Materialer
-Uforlængelig tråd
-1 dej eller metalkugle malet hvid, der fungerer som en pendulbob
-Lineal
-Transportør
-Fotografisk kamera med automatisk strobedisk
-Beslag
-To lyskilder
-Et ark sort papir eller pap
Behandle
Det er nødvendigt at samle figuren for at tage billeder af flere blink i pendulet, når den følger dens sti. For at gøre dette skal du placere kameraet lige over pendulet og den automatiske strobedisk foran linsen.
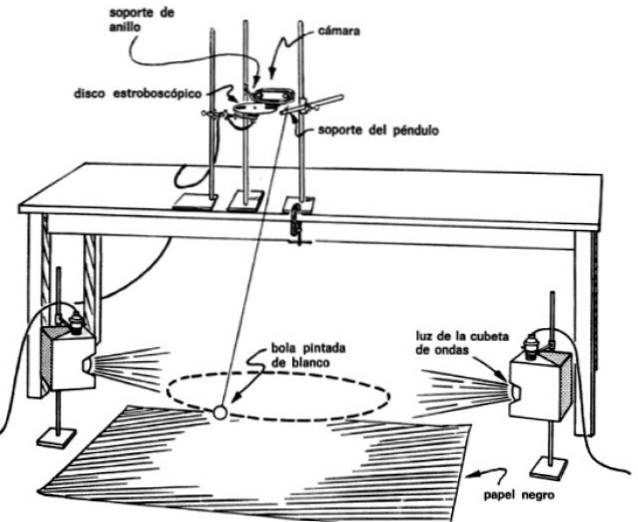
På denne måde opnås billeder med regelmæssige tidsintervaller i pendulet, for eksempel hvert 0,1 eller hvert 0,2 sekund, hvilket gør det muligt at kende den tid, det tog at flytte fra et punkt til et andet..
Du er også nødt til at belyse pendulets masse korrekt og sætte lysene på begge sider. Linsen skal males hvidt for at forbedre kontrasten i baggrunden, som består af et sort papir spredt på jorden.
Nu skal du kontrollere, at pendulet fejer lige store områder på lige tid. For at gøre dette vælges et tidsinterval, og de punkter, der er optaget af pendulet i intervallet, er markeret på papiret..
På billedet er der trukket en linje fra midten af det ovale til disse punkter, og således får vi det første af de områder, der fejes af pendulet, hvilket er omtrent en elliptisk sektor som den vist nedenfor:
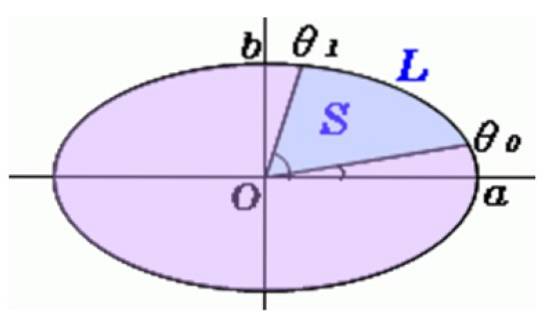
Beregning af arealet af den elliptiske sektion
Vinkler måles med vinkelmåleren θeller Y θ1, og denne formel bruges til at finde S, området for den elliptiske sektor:
S = F (θ1) - F (θeller)
Med F (θ) givet af:

Noter det til Y b er henholdsvis halv- og mindre akser. Læseren behøver kun at bekymre sig om omhyggeligt at måle halvakserne og vinklerne, da der er lommeregnere online for nemt at evaluere dette udtryk..
Hvis du insisterer på at udføre beregningen manuelt, skal du huske at vinklen θ måles i grader, men når du indtaster dataene i regnemaskinen, skal værdierne udtrykkes i radianer.
Derefter skal du markere et andet par punkter, hvor pendulet har vendt det samme tidsinterval, og tegne det tilsvarende område og beregne dets værdi med samme procedure.
Verifikation af loven om lige områder
Endelig er det tilbage at kontrollere, at lovgivningen om områder er opfyldt, dvs. at lige områder fejes på lige tid.
Afviger resultaterne en smule fra det forventede? Det skal altid huskes, at alle målinger ledsages af deres respektive eksperimentelle fejl.
Referencer
- Keisan Online Lommeregner. Område for en elliptisk sektorberegner. Gendannet fra: keisan.casio.com.
- Openstax. Keplers lov om planetarisk bevægelse. Gendannet fra: openstax.org.
- PSSC. Laboratoriefysik. Redaktionel Reverté. Gendannet fra: books.google.co.
- Palen, S. 2002. Astronomi. Schaum-serien. Mcgraw bakke.
- Pérez R. Enkelt system med central styrke. Gendannet fra: francesphysics.blogspot.com
- Stern, D. Keplers tre love om planetbevægelse. Gendannet fra: phy6.org.


Endnu ingen kommentarer