Bloker algebraelementer, eksempler, løste øvelser

Det blok algebra henviser til det sæt af operationer, der udføres gennem blokke. Disse og nogle andre elementer tjener til skematisk at repræsentere et system og let visualisere dets reaktion på et givet input..

Generelt indeholder et system forskellige elektriske, elektroniske og elektromekaniske elementer, og hver enkelt af dem med sin respektive funktion og position i systemet samt den måde, de er relateret på, er skitseret gennem funktionelle blokke.

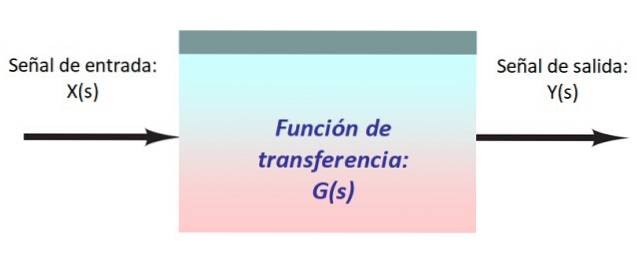
I figuren ovenfor er der et meget simpelt system, der består af et indgangssignal X (s), der kommer ind i blokken med overføringsfunktionen G (s), der ændrer det og producerer output Y (s).

Det er praktisk at repræsentere signalerne og deres vej gennem systemet ved hjælp af pile, der kommer ind og forlader hver blok. Normalt ledes signalstrømmen fra venstre mod højre.

Fordelen ved denne form for skematisk er den visuelle hjælp, den giver til forståelse af systemet, selvom det ikke er en fysisk repræsentation af systemet. Faktisk er blokdiagrammet ikke entydigt, for afhængigt af synspunktet kan flere diagrammer af det samme system endda tegnes..

Det kan også ske, at det samme diagram tjener flere systemer, der ikke nødvendigvis er relateret til hinanden, så længe det tilstrækkeligt beskriver deres adfærd. Der er forskellige systemer, hvis respons er ens i mange henseender, for eksempel et LC-kredsløb (induktorkondensator) og et massefjedersystem..

Artikelindeks

• 1 Hvad er et blokdiagram?
• 2 Elementer af blokdiagrammet
  • 2.1 Signalet
  • 2.2 Blokken
  • 2.3 Summen
  • 2.4 Forgreningspunkt
• 3 Eksempler på blokalgebraregler
  • 3.1 Kaskadeblokke
  • 3.2 Blokke parallelt
  • 3.3 Flyt en optæller til venstre
  • 3.4 Flyt en markør til højre
  • 3.5 Flytning af et forgreningspunkt fra venstre mod højre
  • 3.6 Flyt et forgreningspunkt fra højre til venstre
  • 3.7 Feedback-system
  • 3.8 System med feedback og transducer
• 4 Løst øvelser
  • 4.1 Øvelse 1
  • 4.2 Øvelse 2
• 5 Referencer

Hvad er et blokdiagram?

Systemerne er generelt mere komplicerede end den i figur 1, men blokalgebra giver en række enkle regler til at manipulere systemskemaet og reducere det til sin enkleste version..

Som forklaret i begyndelsen bruger diagrammet blokke, pile og cirkler til at etablere forholdet mellem hver komponent i systemet og strømmen af ​​signaler, der løber gennem det..

Blokalgebra giver dig mulighed for at sammenligne to eller flere signaler ved at tilføje, trække og multiplicere dem samt analysere det bidrag, som hver komponent giver til systemet.

Takket være dette er det muligt at reducere hele systemet til et enkelt indgangssignal, en enkelt overførselsfunktion, der fuldt ud beskriver systemets handling og den tilsvarende udgang..

Blokdiagramelementer

Elementerne i blokdiagrammet er som følger:

Signalet

Signalerne er af meget varieret art, for eksempel er det almindeligt, at det er en elektrisk strøm eller en spænding, men det kan være lys, lyd og mere. Det vigtige er, at det indeholder information om et bestemt system.

Signalet betegnes med et stort bogstav, hvis det er en funktion af variablen s af Laplace-transformationen: X (s) (se figur 1) eller med små bogstaver, hvis det er en funktion af tiden t, som x (t).

I blokdiagrammet er indgangssignalet repræsenteret af en pil rettet mod blokken, mens udgangssignalet, betegnet som Y (s) eller y (t), er angivet med en udgående pil.

Både indgangs- og udgangssignalerne er unikke, og retningen, som informationen flyder, bestemmes af pilens retning. Og algebraen er den samme for en af ​​de to variabler.

Blokken

Blokken er repræsenteret af et kvadrat eller et rektangel (se figur 1) og kan bruges til at udføre operationer eller implementere overføringsfunktionen, som normalt betegnes med store bogstaver G. Denne funktion er en matematisk model, der bruger, som beskriver svaret tilbydes af systemet til et indgangssignal.

Overførselsfunktionen kan udtrykkes i tid t som G (t) eller variablen s som G (s).

Når indgangssignalet X (er) når blokken, ganges det med overførselsfunktionen og omdannes til udgangssignalet Y (er). Matematisk udtrykkes det således:

Y (s) = X (s). G (s)

Tilsvarende er overførselsfunktionen forholdet mellem Laplace-transformationen af ​​udgangssignalet og Laplace-transformationen af ​​indgangssignalet, forudsat at de indledende betingelser for systemet er nul:

G (s) = Y (s) / X (s)

Sumpunkt

Tilføjelsespunktet eller addereren er symboliseret ved en cirkel med et kryds indeni. Det bruges til at kombinere to eller flere signaler ved hjælp af addition og subtraktion. I slutningen af ​​pilen, der symboliserer tegnet, placeres et + tegn direkte, hvis nævnte tegn tilføjes, eller et - tegn, hvis det trækkes fra..

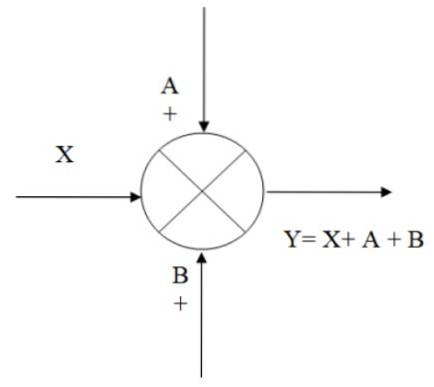
I den følgende figur er der et eksempel på, hvordan addereren fungerer: vi har indgangssignalet X, hvortil signalerne A og B tilføjes, hvilket resulterer i output Y, som er algebraisk ækvivalent med:

Y = X + A + B

Grenpunkt

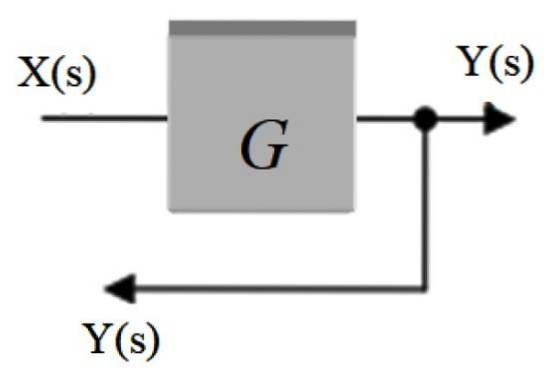
Det kaldes også forgreningspunkt. I det distribueres signalet, der kommer ud af en blok, til andre blokke eller til en adder. Det er repræsenteret af et punkt placeret på signalpilen, og en anden pil kommer ud af det, der omdirigerer signalet til en anden del.

Eksempler på blokalgebraregler

Som forklaret før er ideen at udtrykke systemet ved hjælp af blokdiagrammet og reducere det for at finde den overførselsfunktion, der beskriver det. Følgende er blokalgebra regler for at forenkle diagrammer:

Cascading blokke

Når du har et signal, der passerer successivt gennem G-blokkene₁, G_to, G₃..., reduceres til en enkelt blok, hvis overføringsfunktion er produktet af G₁, G_to, G₃...

I det følgende eksempel kommer signalet X (er) ind i den første blok, og dets output er:

Y₁(s) = X (s) .G₁(s)

Drej Y₁(s) indtast blok G_to(s), hvis output er:

Y_to(s) = X (s) .G₁(s). G_to(s)

Proceduren er gyldig for n kaskadeblokke:

Y_n (s) = X (s). G₁(s) .G_to(s) ... G_n(s)

Parallelle blokke

I diagrammet til venstre forgrener signalet X (s) sig for at komme ind i G-blokkene₁(s) og G_to(s):

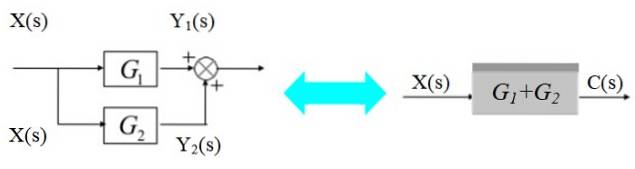
De respektive udgangssignaler er:

Y₁(s) = X (s) .G₁(s)

Y_to(s) = X (s) .G_to(s)

Disse signaler tilføjes sammen for at opnå:

C (s) = Y₁(s) + Y_to(s) = X (s). [G₁(s) + G_to(s)]

Som vist i diagrammet til højre.

Flyt en optæller til venstre

En optæller kan flyttes til venstre for blokken som følger:

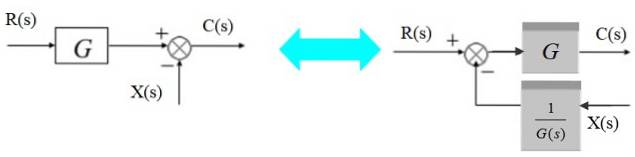
Til venstre er udgangssignalet:

C (s) = R (s). G (s) - X (s)

Tilsvarende til højre:

C (s) = [R (s) - X (s) / G (s)]. G (s)

Flyt en optæller til højre

Adderen kan flyttes til højre for blokken på denne måde:

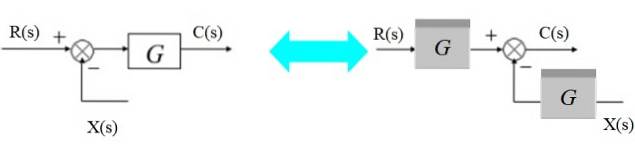
Til venstre har vi: [R (s) - X (s)]. G (s) = C (s)

Og til højre:

R (s). G (s) - X (s). G (s) = C (s)

Flyt et forgreningspunkt fra venstre mod højre

For at flytte forgreningspunktet fra venstre mod højre for blokken, skal du bare observere, at output C (s) til højre er produktet X (s). G (s). Da du vil konvertere det til X (s) igen, skal du gange med det inverse af G (s).

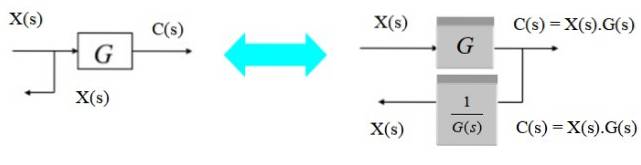
Flyt et forgreningspunkt fra højre til venstre

Alternativt kan forgreningspunktet forskydes fra højre til venstre som følger:

Da vi ved udgangen af ​​grenen ønsker at få C (s), skal du blot indsætte en ny blok G (s) ved et forgreningspunkt til venstre for den originale blok.

Feedback-system

I det følgende system føres udgangssignalet C (s) tilbage gennem markøren til venstre:

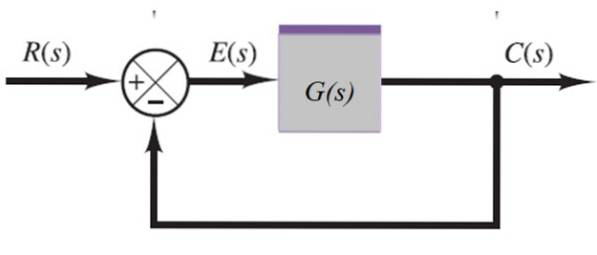
C (s) = E (s). G (s)

Men:

E (s) = R (s) -C (s)

Ved at erstatte dette udtryk i den foregående ligning forbliver det: C (s) = [R (s) -C (s)]. G (s), hvorfra C (s) kan løses:

C (s) + C (s) .G (s) = R (s). G (s) → C (s). [1 + G (s)] = R (s). G (s)

C (s) = R (s). G (s) / [1 + G (s)]

Eller alternativt:

C (s) / R (s) = G (s) / [1 + G (s)]

I grafisk form forbliver det efter forenkling:

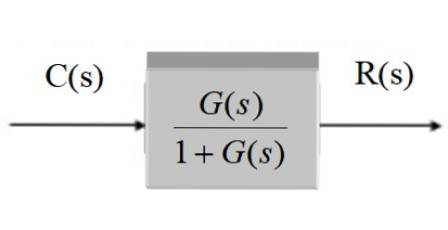
System med feedback og transducer

Transduceren består af overførselsfunktionen H (s):

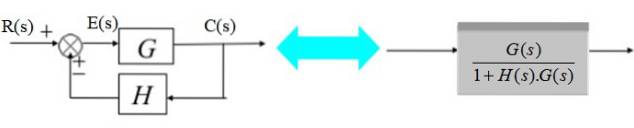
I diagrammet til højre er udgangssignalet C (s):

C (s) = E (s). G (s) med E (s) = R (s) - C (s). H (s)

Derefter:

C (s) = [R (s) - C (s). H (s)]. G (er)

C (s) [1+ H (s) .G (s)] = R (s). G (s)

Derfor kan C (s) løses ved:

C (s) = G (s). R (s) / [1+ H (s) .G (s)]

Og overførselsfunktionen vil være:

G (s) / [1+ H (s) .G (s)]

Som vist i det forenklede diagram til højre.

Løst øvelser

Øvelse 1

Find overførselsfunktionen til følgende system:

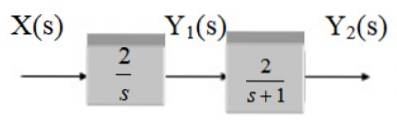
Opløsning

Den behandler to blokke i kaskade, derfor er overførselsfunktionen et produkt af funktionerne G₁ og G_to.

Det skal:

G₁ = 2 / s

G_to = 2 / (s + 1)

Derfor er den ønskede overførselsfunktion:

G (s) = 4 / [s (s + 1)]

Øvelse 2

Reducer følgende system:

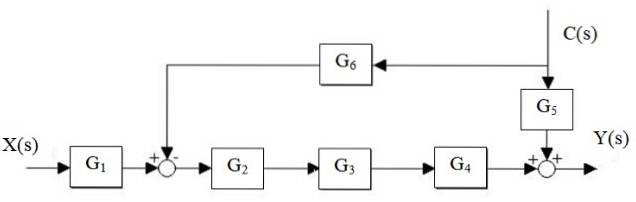
Opløsning

Først reduceres G-kaskaden_to, G₃ og G_4, og parallel G er adskilt₅ og G₆:

Derefter addereren til venstre for blok G_to ⋅G₃ ⋅ G₄ bevæger sig til højre:

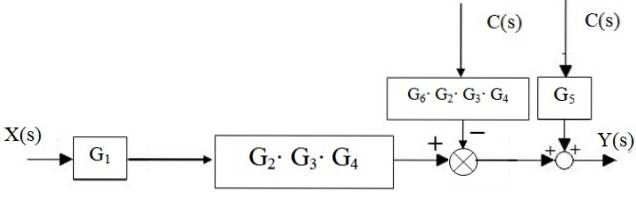
Tilføjere til højre reduceres til kun en samt kaskadeblokkene:

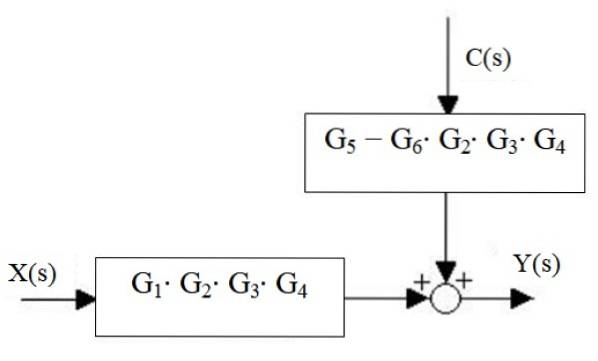
Endelig er systemets output:

Y (s) = X (s) ⋅G₁⋅ G_to ⋅G₃ ⋅ G₄ + C (s) ⋅ [G₅ - G₆ ⋅ G_to ⋅G₃ ⋅ G₄]

Referencer

1. Alaydi, J. Kontrolsystem blokdiagram. Gendannet fra: site.iugaza.edu.ps.
2. Bolton, W. 2006. Kontrolteknik. 2. plads Udgave. Alpha Omega.
3. Cwalinsky, J. Introduktion til systemblokalgebra. Gendannet fra: cedengineering.com.
4. Dademuchconnection. Blokdiagram. Gendannet fra: dademuch.com.
5. Ogata, K. 2010. Moderne kontrolteknik. 5. plads Udgave. Pearson.