Det Fermat grænse er en numerisk metode, der bruges til at få værdien af en linjes hældning, som er tangent til en funktion på et givet punkt i dens domæne. Det bruges også til at opnå kritiske punkter i en funktion. Dets udtryk er defineret som:
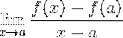
Det er indlysende, at Fermat ikke kendte de grundlæggende faktorer for afledning, men det var hans studier, der fik en gruppe matematikere til at forhøre sig om tangentlinjer og deres anvendelser i beregning..
Artikelindeks
Den består af en tilgang på 2 punkter, der i tidligere forhold danner en sekant linje til funktionen med skæringspunkt i par af værdier.
Ved at nærme sig variablen til værdien "a" tvinges parret til at mødes. På denne måde bliver den tidligere sekante linje tangent til punktet (a; f (a)).
Værdien af kvotienten (x - a), når den evalueres i punkt "a", giver en ubestemmelighed af K-type grænser mellem nul (K / 0). Hvor disse ubestemmelighed kan brydes gennem forskellige factoringteknikker.
De mest anvendte driftsteknikker er:
-Kvadratforskel (ato - bto ) = (a + b) (a - b); Eksistensen af elementet (a-b) indebærer i de fleste tilfælde den faktor, der forenkler udtrykket (x-a) i kvoten for Fermat-grænsen.
- Afslutning af firkanter (axto + bx); Efter afslutning af firkanter opnås et Newton binomium, hvor en af dens 2 faktorer er forenklet med udtrykket (x - a), der bryder ubestemtheden.
- Konjugat (a + b) / (a + b); Multiplikation og deling af udtrykket med konjugatet af en eller anden faktor kan være til stor hjælp for at bryde ubestemmelsen.
- Fælles faktor I mange tilfælde skjuler resultatet af betjening af tælleren af Fermat-grænsen f (x) - f (a) den faktor (x - a), der er nødvendig for at faktorere. Til dette observeres det nøje, hvilke elementer der gentages i hver faktor af udtrykket.
Selvom Fermat-grænsen ikke skelner mellem maksimum og minimum, da den kun kan identificere de kritiske punkter i henhold til dens definition, bruges den ofte til beregning af hætter eller gulve for funktionerne i flyet..
En grundlæggende viden om den grafiske funktionsteori i forbindelse med denne sætning kan være tilstrækkelig til at fastlægge maksimale og minimale værdier mellem funktioner. Faktisk kan bøjningspunkterne defineres ved hjælp af middelværdisætningen ud over Fermats sætning.
Det mest betydningsfulde paradoks for Fermat kom fra at studere den kubiske parabel. Fordi hans opmærksomhed var rettet mod tangentlinjerne i en funktion for et givet punkt, løb han ind i problemet med at definere tangentlinjen ved bøjningspunktet i funktionen.
Det syntes umuligt at bestemme tangentlinjen til et punkt. Således begynder forespørgslen, der vil give anledning til den differentielle beregning. Defineret senere af vigtige eksponenter for matematik.
Undersøgelsen af maksimum og minimum af en funktion var en udfordring for klassisk matematik, hvor en entydig og praktisk metode var nødvendig for at definere disse.
Fermat skabte en metode baseret på driften af små differensværdier, som efter factoring-processer elimineres, hvilket giver plads til den maksimale og minimale værdi, der søges.
Denne variabel skal evalueres i det originale udtryk for at bestemme koordinaten for det nævnte punkt, som sammen med analytiske kriterier vil blive defineret som maksimum eller minimum for udtrykket.
I sin metode bruger Fermat den bogstavelige symbolik af Vieta, som bestod i den eksklusive brug af store bogstaver: vokaler, for ukendte og konsonanter for kendte mængder..
I tilfælde af radikale værdier implementerede Fermat en bestemt proces, som senere ville blive brugt til faktorisering af grænserne for ubestemmelighed uendelighed blandt uendelighed.
Denne proces består i at dividere hvert udtryk med værdien af den anvendte differens. I tilfælde af Fermat brugte han bogstavet E, hvor den værdi, der blev søgt til det kritiske punkt efter at have divideret med E med den højeste magt, blev klar..
Fermat-grænsen er faktisk et af de mindst kendte bidrag på matematikerens lange liste. Hans studier gik fra primtalene for at grundlæggende skabe basis for beregningen.
Til gengæld var Fermat kendt for sine excentriske forhold til hans hypoteser. Det var almindeligt for ham at efterlade en slags udfordring til de andre matematikere på det tidspunkt, da han allerede havde løsningen eller beviset.
Han havde en lang række tvister og alliancer med forskellige tidens matematikere, der elskede eller hadede at arbejde med ham.
Hans sidste sætning var hovedansvarlig for hans verdensberømmelse, hvor han erklærede, at en generalisering af Pythagoras sætning for enhver klasse "n" var det umuligt. Han hævdede at have et gyldigt bevis på det, men døde før han offentliggjorde det.
Denne demonstration måtte vente ca. 350 år. I 1995 sluttede matematikerne Andrew Wiles og Richard Taylor den angst, Fermat efterlod, og viste, at han havde ret gennem et gyldigt bevis for hans sidste sætning.
Definer hældningen af tangentlinjen til kurven f (x) = xto ved punktet (4, 16)
Udskiftning i udtrykket af Fermat-grænsen har vi:
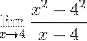
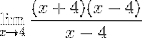
Faktorerne (x - 4) er forenklet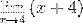
Ved evaluering har du
M = 4 + 4 = 8
Definer det kritiske punkt for udtrykket f (x) = xto + 4x ved hjælp af Fermat-grænsen
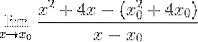
En strategisk gruppering af elementer udføres, der søger at gruppere X-X-parene0
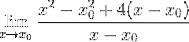
De mindste firkanter er udviklet
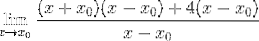
Den fælles faktor X-X observeres0 og ekstraheres
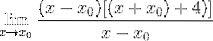
Udtrykket kan nu forenkles og ubestemmelighed brydes
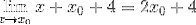
Ved minimumspunkterne er det kendt, at tangentlinjens hældning er lig med nul. På denne måde kan vi udligne det fundne udtryk til nul og løse værdien X0
2 X0 + 4 = 0
x0 = -4/2 = -2
For at få den manglende koordinat er det kun nødvendigt at evaluere punktet i den oprindelige funktion
F (-2) = (-2)to + 4 (-2) = 4-8 = - 4
Det kritiske punkt er P (-2, -4).
Endnu ingen kommentarer