
Invers matrixberegning og løst øvelse
Det Omvendt matrix af en given matrix er det matrixen, der ganges med de originale resultater i identitetsmatrixen. Den omvendte matrix er nyttig til løsning af systemer med lineære ligninger, derfor er det vigtigt at vide, hvordan man beregner den.
Matricer er meget nyttige i fysik, teknik og matematik, da de er et kompakt værktøj til løsning af komplekse problemer. Nytten af matricer forbedres, når de er inverterbare, og deres inverse er også kendt.
Inden for grafisk behandling, Big Data, Data Mining, Machine Learning og andre anvendes effektive og hurtige algoritmer til at evaluere den inverse matrix af nxn-matricer med meget store n, i størrelsesordenen tusinder eller millioner.
For at illustrere brugen af den inverse matrix til håndtering af et system med lineære ligninger starter vi med det enkleste tilfælde af alle: 1 × 1 matricer.
Det enkleste tilfælde: en lineær ligning af en enkelt variabel betragtes som: 2 x = 10.
Ideen er at finde værdien af x, men det vil blive gjort "matrixmæssigt".
Matrixen M = (2), der multiplicerer vektoren (x), er en 1 × 1 matrix, der resulterer i vektoren (10):
M (x) = (10)
Det inverse af matrixen M er betegnet med M-1.
Den generelle måde at skrive dette "lineære system" på er:
M X = B, hvor X er vektoren (x) og B er vektoren (10).
Per definition er den inverse matrix en, der ganges med den oprindelige matrix, resulterer i identitetsmatrix I:
M-1 M = jeg
I det betragtede tilfælde matricen M-1 er matrixen (½), det vil sige M-1 = (½) siden M-1 M = (½) (2) = (1) = I
For at finde den ukendte vektor X = (x) i den foreslåede ligning ganges begge medlemmer med den inverse matrix:
M-1 M (x) = M-1 (10)
(½) (2) (x) = (½) (10)
(½ 2) (x) = (½ 10)
(1) (x) = (5)
(x) = (5)
En ligestilling af to vektorer er nået, som kun er ens, når deres tilsvarende elementer er ens, det vil sige x = 5.
Beregning af det inverse af en matrix
Det, der motiverer beregningen af den inverse matrix, er at finde en universel metode til løsning af lineære systemer såsom det følgende 2 × 2-system:
x - 2 y = 3
-x + y = -2
Ved at følge trinene i 1 × 1-sagen, undersøgt i det foregående afsnit, skriver vi ligningssystemet i matrixform:
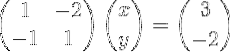
Bemærk, at dette system er skrevet i kompakt vektornotation som følger:
M X = B
hvor
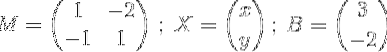
Det næste trin er at finde det omvendte af M.
Metode 1: Brug af Gaussisk eliminering
Den Gaussiske eliminationsmetode vil blive anvendt. Hvilket består i at udføre elementære operationer på matrixens rækker, disse operationer er:
- Multiplicer en række med et ikke-nul tal.
- Tilføj eller træk fra en række en anden række eller multiplum af en anden række.
- Skift rækkerne.
Målet er gennem disse operationer at konvertere den originale matrix til identitetsmatrixen.
Når dette gøres, anvendes i matrix M nøjagtigt de samme operationer til identitetsmatricen. Når der efter flere operationer på rækkerne M er omdannet til den enhedsmatrix, vil den, der oprindeligt var enheden, blive omdannet til den inverse matrix af M, det vil sige M-1.
1- Vi starter processen med at skrive matrixen M og ved siden af den enhedsenheden:
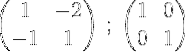
2- Vi tilføjer de to rækker, og vi placerer resultatet i anden række, på denne måde opnår vi et nul i det første element i anden række:
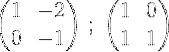
3- Vi gange den anden række med -1 for at opnå 0 og 1 i anden række:
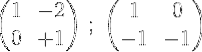
4- Den første række ganges med ½:
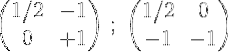
5- Det andet og det første tilføjes, og resultatet placeres i første række:
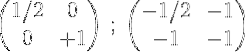
6- For at afslutte processen multipliceres den første række med 2 for at få identitetsmatricen i den første række og den inverse matrix for den oprindelige matrix M i den anden:
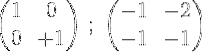
Nemlig:
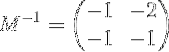
Systemløsning
Når den inverse matrix er opnået, fortsætter vi med at løse ligningssystemet ved at anvende den inverse matrix på begge medlemmer af den kompakte vektorligning:
M-1M X = M-1B
X = M-1B
Som eksplicit ser sådan ud:
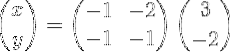
Derefter udføres matrixmultiplikation for at opnå vektor X:
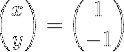
Metode 2: Brug af vedhæftet matrix
I denne anden metode beregnes den inverse matrix startende fra den tilstødende matrix af den oprindelige matrix TIL.
Antag en matrix A givet af:

hvorhenjeg, j er elementet i rækken jeg og kolonnen j af matrixen TIL.
Matrixens sammenhæng TIL det vil blive kaldt Adj (A) og dens elementer er:
annoncejeg, j = (-1)(i + j) ¦Ai, j¦
hvor Ai, j er den komplementære mindre matrix opnået ved at eliminere række i og kolonne j fra den oprindelige matrix TIL. Søjlerne ¦ ¦ angiver, at determinanten beregnes, dvs. ¦Ai, j¦ er determinanten for den komplementære mindre matrix.
Omvendt matrixformel
Formlen til at finde den inverse matrix startende fra den tilstødende matrix i den oprindelige matrix er følgende:
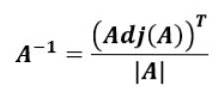
Det vil sige den omvendte matrix af TIL, TIL-1, er transponere af tilslutningen til TIL divideret med determinanten for TIL.
Transponere TILTaf en matrix TIL er den, der opnås ved at udveksle rækker med kolonner, det vil sige, den første række bliver den første kolonne, og den anden række bliver den anden kolonne og så videre, indtil n-rækkerne i den oprindelige matrix er afsluttet.
Træning løst
Lad matrix A være følgende:
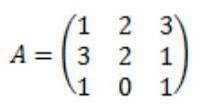
Hvert eneste element i den sammenhængende matrix af A beregnes: Adj (A)
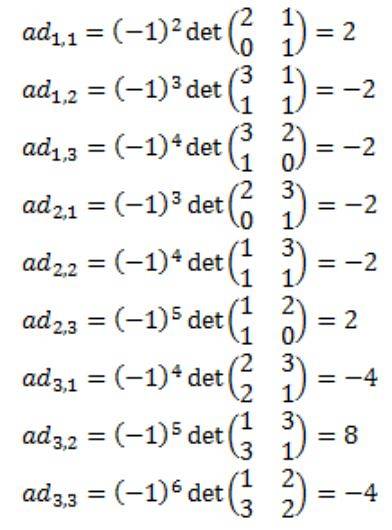
Resultatet er, at den sammenhængende matrix af A, Adj (A) er følgende:
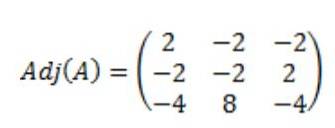
Derefter beregnes determinanten for matrix A, det (A):
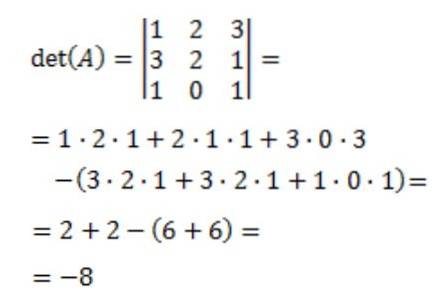
Endelig opnås den inverse matrix af A:
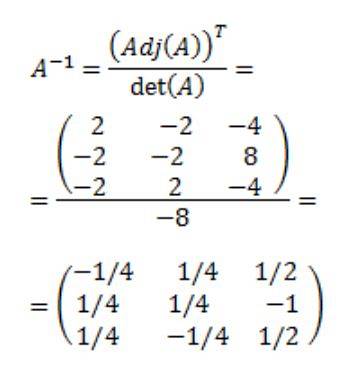
Referencer
- Anthony Nicolaides (1994) Determinants & Matrices. Bestået offentliggørelse.
- Awol Assen (2013) En undersøgelse af beregningen af determinanterne for en 3 × 3
- Casteleiro Villalba M. (2004) Introduktion til lineær algebra. ESIC redaktionelt.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Jenny Olive (1998) Matematik: En studerendes overlevelsesvejledning. Cambridge University Press.
- Richard J. Brown (2012) 30-Second Maths: The 50 Most Mind-Expanding Theories in Mathematics. Ivy presse begrænset.
- Matrix. Lap Lambert Academic Publishing.

Endnu ingen kommentarer