Den har en ortogonal matrix når matrixen ganget med dens transponering resulterer i identitetsmatrixen. Hvis den inverse af en matrix er lig med transponeringen, er den oprindelige matrix ortogonal.
Ortogonale matricer har den egenskab, at antallet af rækker er lig med antallet af kolonner. Rækkevektorerne er også ortogonale enhedsvektorer, og de transponerende rækkevektorer er også.
Når en ortogonal matrix ganges med vektorerne i et vektorrum, frembringer den en isometrisk transformation, en transformation, der ikke ændrer afstandene og bevarer vinklerne.
En typisk repræsentant for ortogonale matricer er rotationsmatricer. Transformationerne af ortogonale matricer på et vektorrum kaldes ortogonale transformationer.
De geometriske transformationer af rotation og refleksion af punkter, der er repræsenteret af deres kartesiske vektorer, udføres ved at anvende ortogonale matricer på de originale vektorer for at opnå koordinaterne for de transformerede vektorer. Det er af denne grund, at ortogonale matricer anvendes i vid udstrækning til computergrafikbehandling..
Artikelindeks
Et array M er ortogonal, hvis den ganges med dens transponering MT returnerer identitetsmatrixen jeg. På samme måde resulterer produktet i transponering af en ortogonal matrix af den originale matrix i identitetsmatrixen:
M MT = MT M = jeg
Som en konsekvens af den foregående udsagn har vi, at transponeringen af en ortogonal matrix er lig med dens inverse matrix:
MT = M-1.
Sættet af dimensionelle ortogonale matricer n x n danner gruppen af ortogonale På). Og delmængden af På) af ortogonale matricer med determinant +1 danner Gruppe af ensartede specialmatricer SU (n). Gruppens matricer SU (n) er matricer, der producerer lineære rotationstransformationer, også kendt som rotationsgruppe.
Lad os vise, at en matrix er ortogonal, hvis og kun hvis rækkevektorerne (eller søjlevektorerne) er ortogonale over for hinanden og af norm 1.
Antag, at rækkerne i en ortogonal matrix n x n er n ortonormale vektorer med dimension n. Hvis betegnet med v1, vto,…., Vn n-vektorerne er tilfredse:
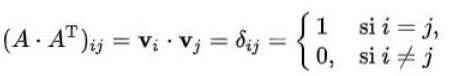
Hvor det er tydeligt, at sættet med rækkevektorer faktisk er et sæt ortogonale vektorer med norm én.
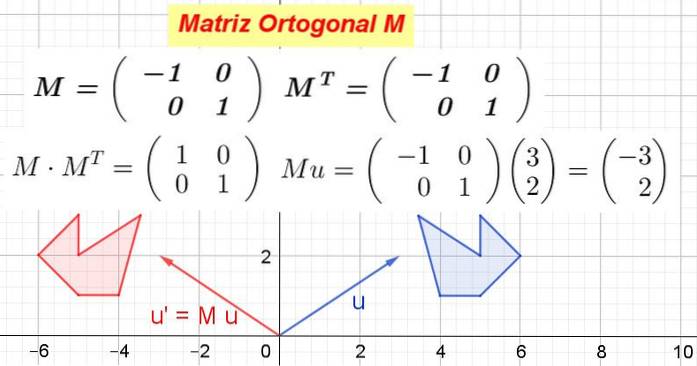
Vis, at den 2 x 2 matrix, der i sin første række har vektoren v1= (-1 0) og i anden række vektoren v2= (0 1) er en ortogonal matrix.
Opløsning: Matricen er bygget M og dens transponering beregnes MT:
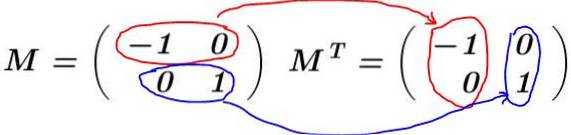
I dette eksempel er arrayet M den er selvtransporteret, dvs. matrixen og dens transponering er identiske. Det multipliceres M ved dens transponering MT:
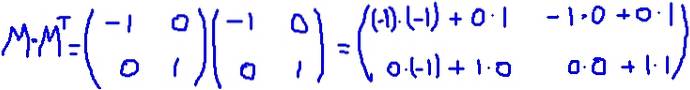
Det er bekræftet, at M MT er lig identitetsmatrixen:
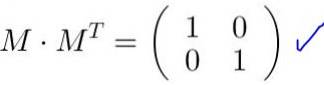
Når matrixen M ganges med koordinaterne for en vektor eller et punkt, der opnås nye koordinater, der svarer til den transformation, som matrixen foretager på vektoren eller punktet.
Figur 1 viser hvordan M transformere vektor eller på eller' og også hvordan M omdanne den blå polygon til den røde polygon. Hvad M er ortogonal er det så en ortogonal transformation, der bevarer afstande og vinkler.
Antag at du har en 2 x 2 matrix defineret i realerne givet af følgende udtryk:
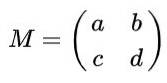
Find de reelle værdier af til, b, c Y d sådan at matrixen M være en ortogonal matrix.
Opløsning: Per definition er en matrix ortogonal, hvis den ganges med dens transponering, opnås identitetsmatricen. Når man husker, at den transponerede matrix hentes fra originalen, udveksler rækker med kolonner, opnås følgende ligestilling:
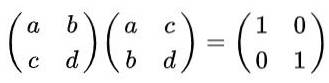
Gennemfør den matrixmultiplikation, vi har:
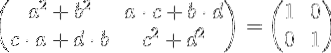
Ligning med elementerne i den venstre matrix med elementerne i identitetsmatricen til højre, vi opnår et system med fire ligninger med fire ukendte a, b, c og d.
Vi foreslår følgende udtryk for a, b, c og d i form af trigonometriske forhold sinus og cosinus:
Med dette forslag og på grund af den grundlæggende trigonometriske identitet tilfredsstilles den første og tredje ligning automatisk i ligningen af matrixelementerne. Den tredje og fjerde ligning er den samme, og i matrixligning efter at have erstattet de foreslåede værdier ser det sådan ud:
hvilket fører til følgende løsning:
Endelig opnås følgende opløsninger til den ortogonale matrix M:
Bemærk, at den første af opløsningerne har determinant +1, så den tilhører gruppen SU (2), mens den anden opløsning har determinant -1 og derfor ikke hører til denne gruppe.
Givet følgende matrix, find værdierne af a og b, så vi har en ortogonal matrix.
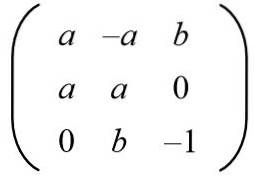
Opløsning: For at en given matrix skal være ortogonal, skal produktet med dets transponering være identitetsmatrixen. Derefter udføres matrixproduktet for den givne matrix med dens transponerede matrix, hvilket giver følgende resultat:
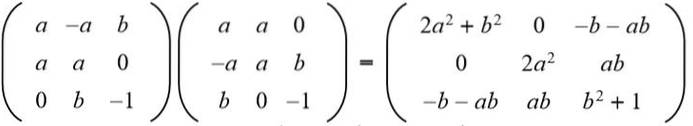
Derefter sidestilles resultatet med 3 x 3 identitetsmatrixen:
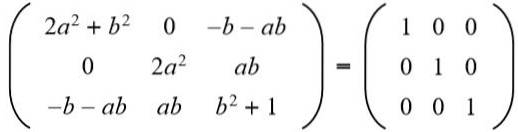
I anden række tredje kolonne har vi (a b = 0), men til det kan ikke være nul, for i så fald ville ligestillingen mellem elementerne i anden række og anden kolonne ikke være opfyldt. Så nødvendigvis b = 0. Udskiftning b for værdien 0 har vi:
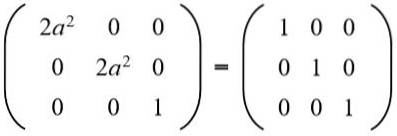
Derefter er ligningen løst: 2a ^ 2 = 1, hvis løsninger er: + ½√2 og -½√2.
Tager den positive løsning til til følgende ortogonale matrix opnås:
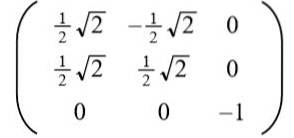
Læseren kan let kontrollere, at rækkevektorerne (og også søjlevektorerne) er ortogonale og enhedsløse, dvs. ortonormale.
Bevis at matrixen TIL hvis rækkevektorer er v1 = (0, -1 0), v2 = (1, 0, 0) Y v3 = (0 0 -1) er en ortogonal matrix. Find også, hvordan vektorerne i den kanoniske base transformeres Jeg J K til vektorer u1, u2 Y u3.
Opløsning: Det skal huskes, at elementet (i, j) i en matrix ganget med dets transponering er prikproduktet af vektoren i række (i) med den i kolonnen (j) i transponeringen. Desuden er dette produkt lig med Kronecker-deltaet, hvis matrixen er ortogonal:
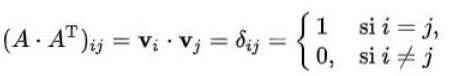
I vores tilfælde ser det sådan ud:
v1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1
v2 • v2 = 1 × 1 + 0x0 + 0x0 = 1
v3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1
v1 • v2 = 0x1 + (-1) x0 + 0x0 = 0
v2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0
v2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0
v3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0
v1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0
v3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0
Med hvilket det er vist, at det er en ortogonal matrix.
Hvad mere er u1 = A i = (0, 1, 0); u2 = A j = (-1, 0, 0) og endelig u3 = A k = (0, 0, -1)
Endnu ingen kommentarer