
Bohr atommodel karakteristika, postulater, begrænsninger

Det Bohr atommodel er den danske fysiker Niels Bohrs (1885-1962) opfattelse af atomets struktur, udgivet i 1913. I Bohr-atomet besætter elektronerne omkring kernen kun visse tilladte baner takket være en begrænsning kaldet kvantisering.
For Bohr var billedet af atomet som et miniaturesolsystem med elektroner, der kredser omkring kernen, ikke helt i overensstemmelse med det faktum, at elektriske ladninger, når de accelereres, udstråler energi..
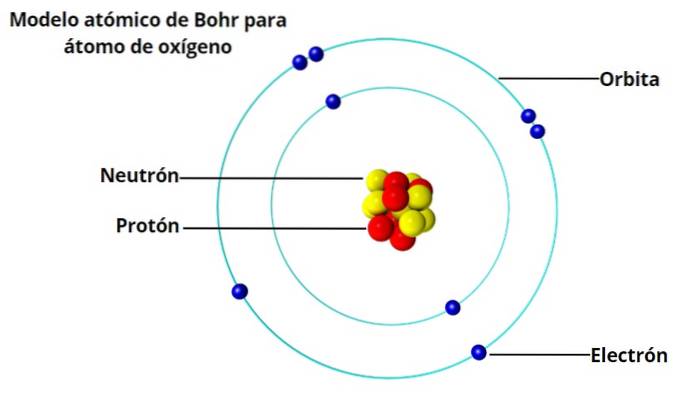
Et sådant atom ville ikke være stabilt, fordi det ville ende med at kollapse før eller senere, fordi elektronerne ville spiralere mod kernen. Og på det tidspunkt havde de karakteristiske lysmønstre, som brint og andre gasser udsender ved opvarmning, været kendt i 50 år..
Mønsteret eller spektret består af en række lyse linjer med visse meget specifikke bølgelængder. Og brintatomet kollapser ikke, når det udsender lys.
For at forklare, hvorfor atomet er stabilt på trods af at det er i stand til at udstråle elektromagnetisk energi, foreslog Bohr, at vinkelmoment kun kunne vedtage bestemte værdier og derfor også energi. Dette menes med kvantisering.
Ved at acceptere, at energien blev kvantiseret, ville elektronen have den nødvendige stabilitet for ikke at skynde sig mod kernen, der ødelagde atomet..
Og atomet udstråler kun lysenergi, når elektronen overgår fra en bane til en anden, altid i diskrete størrelser. På denne måde forklares tilstedeværelsen af emissionsmønstre i brint..
Bohr komponerede således en vision af atomet ved at integrere velkendte begreber fra klassisk mekanik med nyopdagede, såsom Plancks konstant, fotonet, elektronen, atomkernen (Rutherford havde været Bohrs mentor) og ovennævnte spektrum af spørgsmål.
Artikelindeks
- 1 De vigtigste egenskaber ved Bohr-modellen
- 1.1 Beregning af radius for elektronens bane
- 2 Postulater af Bohrs atommodel
- 2.1 Elektroner beskriver cirkulære stier
- 2.2 Vinkelmomentet kvantiseres
- 2.3 Elektroner udsender eller absorberer fotoner, når de går fra en energitilstand til en anden
- 3 Begrænsninger
- 4 Artikler af interesse
- 5 Referencer
Hovedtræk ved Bohr-modellen
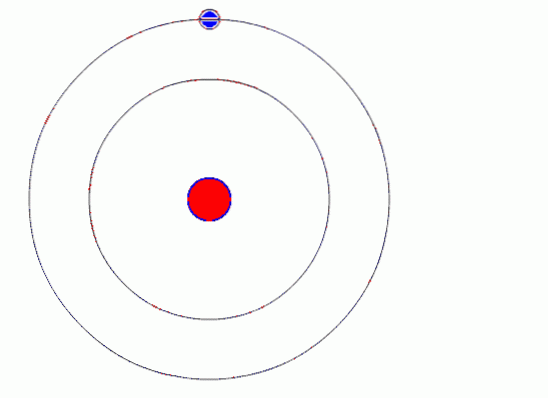
Bohrs atommodel antager, at elektronen bevæger sig i en cirkulær bane omkring kernen ved virkningen af Coulombs elektrostatiske tiltrækningskraft og foreslår, at elektronens vinkelmoment kvantiseres.
Lad os se, hvordan man integrerer begge begreber i matematisk form:
Lad L være størrelsen af vinkelmomentet, m massen af elektronen, v elektronens hastighed og r kredsløbets radius. For at beregne L har vi:
L = m⋅r⋅v
Bohr foreslog, at L var lig med heltalsmultipler af den konstante h / 2π, hvor h er den Planck er konstant, introduceret for kort tid siden af fysikeren Max Planck (1858-1947), da han løste problemet med den energi, der udsendes af en sort krop, et teoretisk objekt, der absorberer alt det indfaldende lys.
Dens værdi er h = 6,626 × 10−34 J ・ s, mens en h / 2π betegnes som ħ, hvad der læses "H bar".
Derfor forbliver vinkelmomentet L:
m⋅r⋅v = nħ, med n = 1,2, 3 ...
Og fra denne tilstand udledes radierne af banerne, der er tilladt for elektronen, som vi vil se nedenfor.
Beregning af radius for elektronens bane
I det følgende antager vi de enkleste atomer: brint, der består af en enkelt proton og en elektron, begge med en ladning af størrelsen e.
Den centripetale kraft, der holder elektronen i sin cirkulære bane, tilvejebringes ved elektrostatisk tiltrækning, hvis størrelse F er:
F = keto/ rto
Hvor k er den elektrostatiske konstant af Coulombs lov og r elektron-protonafstanden. At vide, at i en cirkulær bevægelse centripetal acceleration vedc er givet ved forholdet mellem kvadratet af hastigheden og afstanden r:
tilc = vto / r
Ifølge Newtons anden lov er nettokraften produktet af massen m og accelerationen:
mvto/ r = keto/ rto
Forenkling af radius r opnår vi:
m⋅vtor = keto
Ved at kombinere dette udtryk med vinkelmomentet har vi et ligningssystem givet af:
1) mvtor = keto
2) r = n ħ/ mv
Ideen er at løse systemet og bestemme r, radius af den tilladte bane. En lille elementær algebra fører til svaret:
r = (nħ)to / k⋅m⋅eto
Med n = 1, 2, 3, 4, 5 ...
For n = 1 har vi den mindste af radierne, kaldet Bohr radius tileller med en værdi på 0,529 × 10−10 m. Radierne for de andre baner udtrykkes i form af tileller.
På denne måde introducerer Bohr det vigtigste kvantetal n, bemærker, at de tilladte radier er en funktion af Plancks konstant, den elektrostatiske konstant og massen og ladningen af elektronen.
Bohrs atommodel postulerer

Bohr kombinerer dygtigt Newtons mekanik med nye opdagelser, der konstant fandt sted i anden halvdel af det nittende og tidlige tyvende århundrede. Blandt dem det revolutionære koncept af "kvanten", som Planck selv hævdede ikke var meget overbevist om.
Gennem sin teori var Bohr i stand til på tilfredsstillende måde at forklare serien i hydrogenspektret og forudsige energiemissioner i det ultraviolette og infrarøde område, som endnu ikke var blevet observeret..
Vi kan sammenfatte dets postulater som følger:
Elektroner beskriver cirkulære stier
Elektronen drejer sig om kernen i en stabil cirkulær bane med ensartet cirkulær bevægelse. Bevægelsen skyldes den elektrostatiske tiltrækning, som kernen udøver på den.
Vinkelmomentet kvantiseres
Elektronens vinkelmoment kvantiseres i henhold til udtrykket:
L = mvr = nħ
Hvor n er et heltal: n = 1, 2, 3, 4 ..., hvilket fører til, at elektronen kun kan være i bestemte definerede kredsløb, hvis radier er:
r = (n ħ)to / k m eto
Elektroner udsender eller absorberer fotoner, når de går fra en energitilstand til en anden
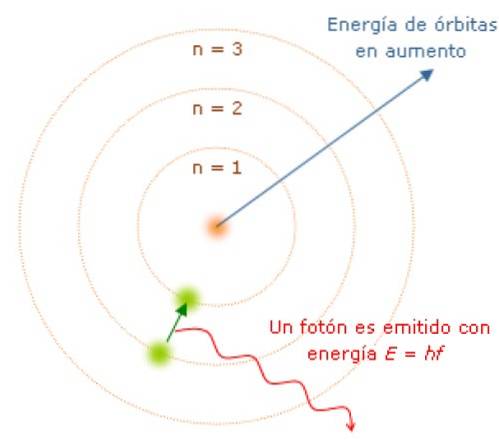
Da vinkelmomentet kvantiseres, er energien E. Det kan vises, at E er givet ved:


Elektron volt, eller eV, er en anden enhed for energi, der er meget brugt i atomfysik. Det negative tegn i energien sikrer kredsløbets stabilitet, hvilket indikerer, at der skal arbejdes for at adskille elektronen fra denne position..
Mens elektronen er i sin bane, absorberer eller udsender den ikke lys. Men når det springer fra en højere energibane til en lavere, gør det det..
Frekvensen f for det udsendte lys afhænger af forskellen mellem banernes energiniveauer:
E = hf = Einitial - Eendelig
Begrænsninger
Bohr-modellen har visse begrænsninger:
-Det anvendes kun med succes på hydrogenatomet. Forsøg på at anvende det på mere komplekse atomer mislykkedes.
-Det svarer ikke på, hvorfor nogle baner er stabile, og andre ikke er. Det faktum, at energien i atomet blev kvantificeret, fungerede meget godt, men modellen gav ingen grund, og det var noget, der forårsagede forskere ubehag..
-En anden vigtig begrænsning er, at den ikke forklarede de ekstra linjer, der udsendes af atomer i nærvær af elektromagnetiske felter (Zeeman-effekt og Stark-effekt). Eller hvorfor nogle linjer i spektret var mere intense end andre.
-Bohr-modellen overvejer heller ikke relativistiske effekter, som det er nødvendigt at tage i betragtning, da det eksperimentelt blev bestemt, at elektroner er i stand til at nå hastigheder, der er helt tæt på lysets i vakuum..
-Det antages, at det er muligt at kende nøjagtigt positionen og hastigheden af elektronen, men hvad der faktisk beregnes er sandsynligheden for, at elektronen indtager en bestemt position.
På trods af sine begrænsninger var modellen meget vellykket på det tidspunkt, ikke kun for at integrere nye opdagelser med allerede kendte elementer, men også fordi den rejste nye spørgsmål, hvilket gjorde det klart, at vejen til en tilfredsstillende forklaring af atomet lå i kvantemekanik..
Artikler af interesse
Schrödingers atommodel.
Atomic de Broglie model.
Chadwick Atomic Model.
Heisenberg atommodel.
Perrins atommodel.
Thomsons atommodel.
Dalton atommodel.
Dirac Jordan atommodel.
Atomisk model af Democritus.
Atomisk model af Leucippus.
Sommerfeld atommodel.
Nuværende atommodel.
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 2. Mc Graw Hill.
- Bohrs atommodel. Gendannet fra: sgpwe.izt.uam.mx.
- Serway, R. (2008). Fysik til videnskab og teknik. Bind 2. 7. Ed. Cengage Learning.
- Thomas Griffith, W. 2007. Konceptuel fysik. Mcgraw bakke.
- Tomé, C. Begrænsningerne ved Bohr-modellen. Notebooks of Scientific Culture. Gendannet fra: culturacientifica.com.



Endnu ingen kommentarer