
Dirac Jordan atommodel egenskaber og postulater

Det Atommodel fra Dirac-Jordan er den relativistiske generalisering af den Hamilton-operatør i ligningen, der beskriver elektronens kvantebølgefunktion. I modsætning til den tidligere model, Schrodinger, er det ikke nødvendigt at påtvinge spin ved hjælp af Pauli-udelukkelsesprincippet, da det forekommer naturligt.
Derudover indeholder Dirac-Jordan-modellen relativistiske korrektioner, spin-orbit-interaktionen og Darwin-udtrykket, der tegner sig for den fine struktur af atomets elektroniske niveauer..

Fra 1928 satte forskerne Paul A. M. Dirac (1902-1984) og Pascual Jordan (1902-1980) sig i gang med at generalisere kvantemekanikken udviklet af Schrodinger for at inkludere Einsteins rettelser af særlig relativitetsteori..
Dirac starter fra Schrodinger-ligningen, som består af en differentiel operatør, kaldet en Hamiltonian, der fungerer på en funktion kendt som elektronbølgefunktionen. Imidlertid tog Schrodinger ikke hensyn til de relativistiske effekter.
Løsningerne til bølgefunktionen giver os mulighed for at beregne de regioner, hvor elektronen med en vis grad af sandsynlighed findes omkring kernen. Disse regioner eller zoner kaldes orbitaler og afhænger af bestemte diskrete kvantetal, der definerer elektronens energi og vinkelmoment.
Artikelindeks
- 1 Postulater
- 1.1 De fire postulater fra Dirac
- 2 Dirac-ligningen
- 2.1 Dirac-Jordan-atomet
- 2.2 Relativistiske korrektioner til energispektret
- 3 Artikler af interesse
- 4 Referencer
Postulater
I kvantemekaniske teorier, uanset om de er relativistiske eller ej, er der intet begreb om baner, da hverken elektronens position eller hastighed kan specificeres samtidigt. Og desuden fører angivelse af en af variablerne til total upræcision i den anden..
Hamiltonian er for sin del en matematisk operator, der virker på kvantebølgefunktionen og er bygget ud fra elektronens energi. For eksempel har en fri elektron total energi E, som afhænger af dens lineære momentum s dermed:
E = (sto) / 2m
For at konstruere Hamiltonian starter vi med dette udtryk og erstatning s af kvanteoperatøren for momentum:
s = -i ħ ∂ / ∂r
Det er vigtigt at bemærke, at vilkårene s Y s er forskellige, da den første er momentum, og den anden er differentiel operatør forbundet med momentum.
Derudover er i den imaginære enhed og ħ Planck-konstanten divideret med 2π, på denne måde opnås den Hamilton-operatør H af det frie elektron:
H = (ħto/ 2m) ∂to / ∂rto
For at finde elektronen fra Hamilton i atomet skal du tilføje interaktionen mellem elektronen og kernen:
H = (ħ2 / 2m) ∂to / ∂rto - eΦ (r)
I det foregående udtryk -e er elektronens elektriske ladning og Φ (r) er det elektrostatiske potentiale produceret af den centrale kerne.
Nu fungerer operatøren H på bølgefunktionen ψ i henhold til Schrodinger-ligningen, som er skrevet således:
H ψ = (i ħ ∂ / ∂t) ψ
Diracs fire postulater
Første postulat: Den relativistiske bølgeligning har samme struktur som Schrodinger-bølgeligning, hvad der ændrer sig er H:
H ψ = (i ħ ∂ / ∂t) ψ
Andet postulat: Den Hamilton-operatør er konstrueret ud fra Einsteins energimomentforhold, som er skrevet som følger:
E = (mto c4 + sto cto)1/2
I det foregående forhold, hvis partiklen har momentum p = 0, har vi den berømte ligning E = mcto som relaterer hvileenergien af enhver massepartikel m til lysets hastighed c.
Tredje postulat: for at opnå den Hamilton-operatør anvendes den samme kvantiseringsregel, der anvendes i Schrodinger-ligningen:
s = -i ħ ∂ / ∂r
I begyndelsen var det ikke klart, hvordan man skulle håndtere denne differentiale operatør, der handlede inden for en kvadratrod, så Dirac satte sig for at opnå en lineær Hamilton-operatør på momentumoperatøren og derfra opstod hans fjerde postulat.
Fjerde postulat: for at slippe af med kvadratroden i den relativistiske energiformel, foreslog Dirac følgende struktur for E.to:
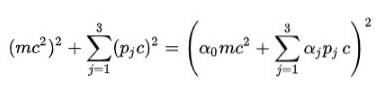
Selvfølgelig er det nødvendigt at bestemme alfakoefficienterne (α0, α1, α2, α3) for at dette skal være sandt.
Diracs ligning
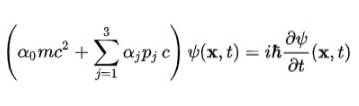
I sin kompakte form betragtes Dirac-ligningen som en af de smukkeste matematiske ligninger i verden:
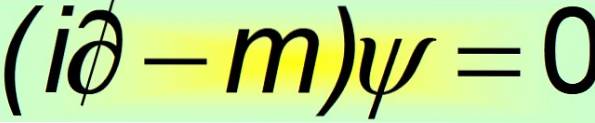
Og det er når det bliver klart, at den konstante alfa ikke kan være skalære størrelser. Den eneste måde, hvorpå det fjerde postulats ligestilling er opfyldt, er at de er 4 × 4 konstante matricer, der er kendt som Dirac matricer:
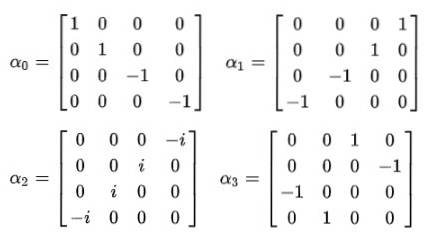
Det observeres straks, at bølgefunktionen ophører med at være en skalarfunktion og bliver en kaldet firekomponentvektor spinor:
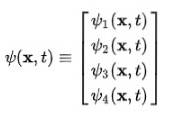
Dirac-Jordan-atomet
For at opnå atommodellen er det nødvendigt at gå fra ligningen af den frie elektron til elektronens i det elektromagnetiske felt produceret af atomkernen. Denne interaktion tages i betragtning ved at inkorporere det skalære potentiale Φ og vektorpotentialet TIL i Hamiltonian:
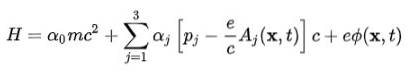
Bølgefunktionen (spinor), der skyldes inkorporering af denne Hamilton, har følgende egenskaber:
- Den opfylder speciel relativitet, da den tager højde for elektronens indre energi (første periode af det relativistiske Hamiltonian)
- Den har fire løsninger svarende til de fire komponenter i spinor
- De to første løsninger svarer til den ene til spin + ½ og den anden til spin - ½
- Endelig forudsiger de to andre løsninger eksistensen af antimateriale, da de svarer til positroner med modsatte spins..
Den store fordel ved Dirac-ligningen er, at korrektionerne til den grundlæggende Schrodinger Hamiltonian H (o) kan opdeles i flere udtryk, som vi viser nedenfor:
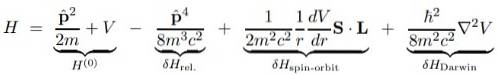
I det foregående udtryk er V det skalære potentiale, da vektorpotentialet TIL er nul, hvis den centrale proton antages at være stationær og derfor ikke vises.
Årsagen til, at Dirac-korrektionerne til Schrodinger-løsninger i bølgefunktionen er subtile. De stammer fra det faktum, at de sidste tre termer af den korrigerede Hamiltonian deles med lysets hastighed c i kvadrat, et enormt tal, hvilket gør disse udtryk numerisk små.
Relativistiske korrektioner til energispektret
Ved hjælp af Dirac-Jordan-ligningen finder vi korrektioner til elektronens energispektrum i hydrogenatomet. Korrektioner for energi i atomer med mere end en elektron i omtrentlig form findes også gennem en metode kendt som forstyrrelsesteori..
På lignende måde tillader Dirac-modellen at finde den fine strukturkorrektion i brintenerginiveauer..
Imidlertid opnås endnu mere subtile korrektioner såsom hyperfin struktur og lamskift fra mere avancerede modeller som f.eks kvantefeltsteori, som blev født netop af bidrag fra Dirac-modellen.
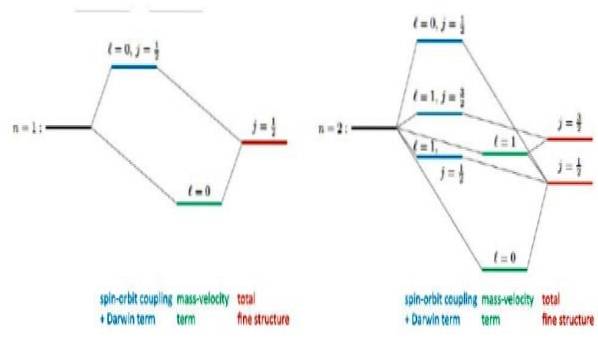
Følgende figur viser, hvordan Diracs relativistiske korrektioner til energiniveauer ser ud:
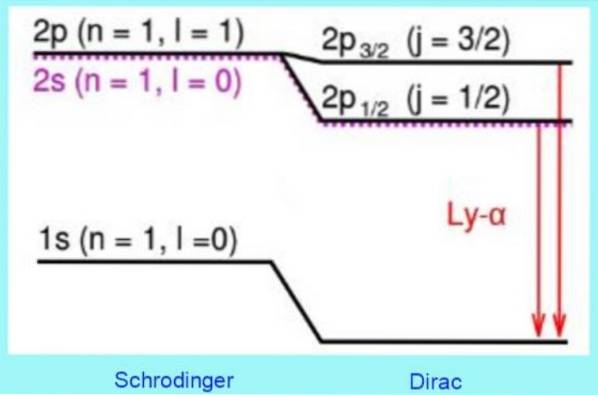
F.eks. Forudsiger løsninger til Dirac-ligningen korrekt et observeret skift på niveau 2s. Det er den velkendte korrektion af fin struktur i Lyman-alfa-linjen i hydrogenspektret (se figur 3).
Forresten er den fine struktur navnet i atomfysik til fordobling af linjerne i atomers emissionsspektrum, hvilket er en direkte konsekvens af elektronisk spin..
Artikler af interesse
Atomic de Broglie model.
Chadwick Atomic Model.
Heisenberg atommodel.
Perrins atommodel.
Thomsons atommodel.
Dalton atommodel.
Schrödingers atommodel.
Atomisk model af Democritus.
Atomisk model af Leucippus.
Bohr atommodel.
Nuværende atommodel.
Referencer
- Atomteori. Gendannet fra wikipedia.org.
- Elektronmagnetisk øjeblik. Gendannet fra wikipedia.org.
- Quanta: En håndbog med begreber. (1974). Oxford University Press. Gendannet fra Wikipedia.org.
- Dirac Jordan atommodel. Gendannet fra prezi.com.
- Det nye kvanteunivers. Cambridge University Press. Gendannet fra Wikipedia.org.


Endnu ingen kommentarer