
Uniform cirkulær bevægelse (M.C.U.) formler, egenskaber

En partikel har cirkulær bevægelse uniform (M.C.U.) når dens bane er en omkreds, og den også bevæger den med konstant hastighed. Mange genstande såsom dele af maskiner og motorer har for eksempel denne form for bevægelse, blandt hvilke computerharddiske, ventilatorblade, aksler og mange andre ting skiller sig ud..
Ensartet cirkulær bevægelse er også en god tilnærmelse til bevægelsen af nogle himmellegemer såsom Jorden. Faktisk er jordens bane elliptisk, som angivet af Keplers love. Banens excentricitet er imidlertid lille, og som en første tilnærmelse kan den betragtes som cirkulær, hvilket forenkler nogle beregninger, såsom at finde jordens hastighed, når den bevæger sig rundt om solen..
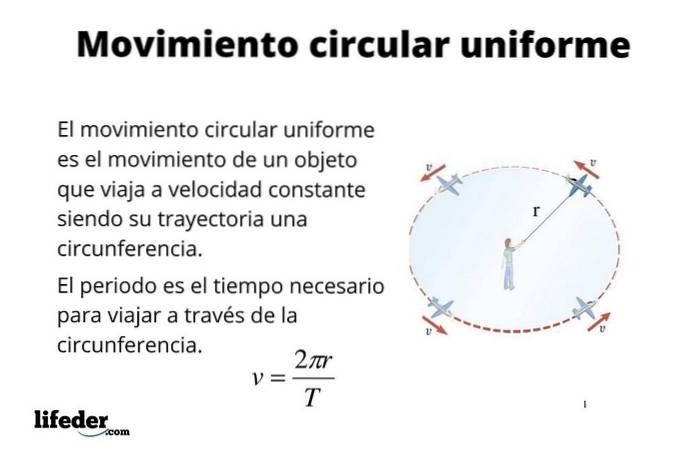
Ved beskrivelse af ensartet cirkulær bevægelse anvendes de samme parametre som i retlinet bevægelse, nemlig: position, forskydning, tid, hastighed og acceleration..
Acceleration? Ja, ja, ensartet cirkulær bevægelse accelereres, selvom dens hastighed v være konstant. Dette er fordi hastigheden v, hvilket er en vektor, og det er derfor, det er fed, kontinuerligt ændrer sin retning, når objektet eller partiklen roterer. Enhver ændring i v produceres ved en acceleration, som, som det ses, er rettet mod midten af den cirkulære sti.
Ensartet cirkulær bevægelse er bevægelse i planet xy, derfor er det en bevægelse i to dimensioner. Det er imidlertid muligt at udtrykke det mere behageligt ved hjælp af den vinkel θ, som partiklen fejer, målt i forhold til den vandrette akse eller en anden passende referenceakse..
Selvom det er et udvidet objekt, fejer dets partikler altid den samme vinkel, selvom de har forskellige koordinater. (x, y).
Artikelindeks
- 1 Egenskaber for ensartet cirkulær bevægelse
- 2 Formler for ensartet cirkulær bevægelse
- 2.1 Positionsvektor
- 2.2 Vinkelhastighed og lineær hastighed
- 2.3 Centripetal acceleration
- 2.4 Periode og hyppighed
- 3 Eksempler på ensartet cirkulær bevægelse
- 3.1 Jordens bevægelse
- 3.2 Partikler på kanten af en disk
- 3.3 Hubble-rumteleskop
- 3.4 Centrifuger
- 3.5 Havesprinklere
- 3.6 Sport
- 4 Øvelse løst
- 5 Referencer
Karakteristika for ensartet cirkulær bevægelse
Kendetegnene ved ensartet cirkulær bevægelse kan opsummeres som følger:
-Banen er en omkreds, derfor er den en bevægelse i planet.
-Farten v er konstant, men hastigheden v nej, fordi det konstant ændrer retning og retning for at imødekomme mobilens tur.
-Hastighedsvektoren v er altid tangentialt for omkredsen og vinkelret på radial retning.
-Vinkelhastigheden ω er konstant.
-På trods af at det er ensartet, er der en acceleration for at forklare disse ændringer i hastighedsretningen. Denne acceleration er den centripetale acceleration.
-Centripetal acceleration og hastighed er vinkelret på hinanden.
-Det er en periodisk eller gentagen bevægelse, derfor er periode- og frekvensstørrelser defineret for den.
Ensartede cirkulære bevægelsesformler
I denne ordning er der en partikel P, der drejer mod uret med MCU i henhold til retning og følelse af hastighedsvektoren v tegnet.
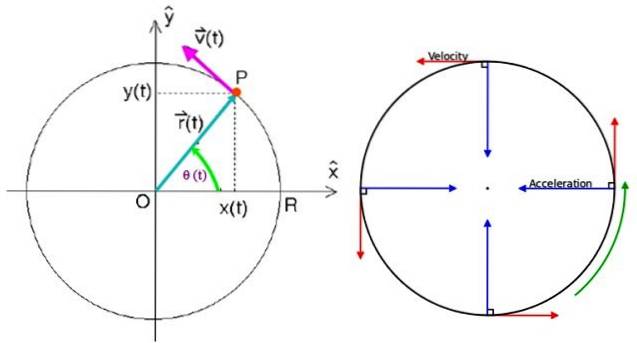
For at specificere positionsvektoren er det nødvendigt at have et referencepunkt, og det ideelle punkt er centrum for omkredsen O, der falder sammen med centrum af det kartesiske koordinatsystem i xy-planet.
Positionsvektor
Det betegnes som r (t) og er rettet fra oprindelsen til det punkt P, hvor partiklen er placeret. På et givet øjeblik t, i kartesiske koordinater, er det skrevet som:
r (t) = x (t) jeg + og T) j
Hvor jeg Y j er enhedsvektorerne vinkelrette i retningerne x og Y henholdsvis. Fra grafen kan det ses, at vektormodulet r (t) altid værd R, omkredsenes radius. Hvis θ er den dannede vinkel r med den vandrette akse er positionen lig med:
r (t) = [Rcos θ(t)] jeg +[Rsen θ(t)] j
Den vinkel, den danner r (t) med den vandrette akse er en central vinkel, og dens værdi er:
θ = s / R
Hvor s er bue af omkreds, og R radius. Den nævnte vinkel θ er en funktion af tiden, så den kan skrives θ = θ (t), opkald vinkelposition.
Da hastigheden er konstant, beskriver partiklen lige vinkler i lige tid og i analogi med den ensartede retlinede bevægelse, skrives det:
θ = θ (t) = θeller + .t
Her θeller er startvinklen målt i radianer i forhold til referenceaksen, den kan være 0 eller en hvilken som helst værdi, og ω er vinkelhastigheden.
Vinkelhastighed og lineær hastighed
Vinkelhastighed er det første afledte af vinkelposition og betegnes som ω. Dens værdi er konstant for ensartet cirkulær bevægelse, da lige vinkler fejes på lige tid. Med andre ord:

Enhederne med lineær hastighed i ensartet cirkulær bevægelse er de samme som for lineær bevægelse: m / s (i SI International System), km / t, cm / s og andre..
Centripetal acceleration
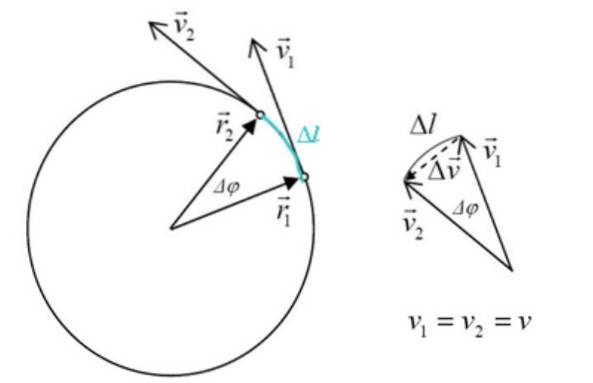
I nedenstående figur er der en partikel, der bevæger sig med uret rundt omkredsen med konstant hastighed. Dette betyder, at hastighedsvektoren altid har samme modul, men det ændrer retning for at imødekomme omkredsen.

Enhver ændring i hastighed resulterer i acceleration, som pr. Definition er:

Trekanten dannet af vto, v1 og Δv svarer til sidetrekanten rto, r1 og Δl, hvor Δφ er den centrale vinkel. Størrelsen af rto Y r1 de er de samme, så:
rto = r1 = r
Derefter har vi af begge trekanter disse forhold for vinklen:
Δφ = Δr / r; Δφ = Δv / v
Den fede type er ikke nødvendig, da målingen på vinklen afhænger af størrelsen af disse vektorer. Ved at matche de tidligere udtryk følger det:





Periode og hyppighed
Da den cirkulære bevægelse er gentagne, er perioden defineret T det samme som den tid det tager for mobilen at foretage en fuldstændig drejning. Da længden af omkredsen af radius R er 2πR, er vinklen fejet i radianer ved fuld drejning 2π radianer, og det tager tid T, er vinkelhastigheden:
ω = 2π / T
T = 2π / ω
Perioden med ensartet cirkulær bevægelse måles i sekunder i det internationale system.
For sin del frekvensen F er antallet af drejninger pr. tidsenhed og er periodens gensidige eller inverse:
f = n / t = 1 / T
Frekvensenheden i det internationale system er s-1.
Eksempler på ensartet cirkulær bevægelse
Mange genstande roterer for at producere forskellige effekter: hjul, skiver og turbiner. Når driftshastigheden er nået, udføres rotation normalt med en konstant hastighed. Cirkulær bevægelse er så almindelig i hverdagen, at du næsten aldrig tænker på det, så her er nogle nære eksempler, der illustrerer det meget godt:
Jordens bevægelse

Jorden og de andre planeter i solsystemet bevæger sig i elliptiske baner med lille excentricitet undtagen kviksølv, hvilket betyder, at det i den første tilnærmelse kan antages, at deres bevægelse er ensartet cirkulær.
Med dette har du en god idé om oversættelseshastigheden omkring Solen, da i tilfælde af Jorden er bevægelsesperioden kendt: et år eller 365 dage..
Partikler på kanten af en disk

Partiklerne, der roterer på kanten af en gammel pladespiller eller bladet på en fan, følger en ensartet cirkulær bevægelse, når enheden når sin afspilningshastighed.
Hubble-rumteleskop

Hubble-rumteleskopet cirkler jorden omkring 7550 m / s.
Centrifuger
Vaskemaskinerne udfører en centrifugeringsproces for at klemme tøjet, der består i at rotere beholdertromlen i høj hastighed. Tørretumblerne roterer også i en periode i en ensartet cirkulær bevægelse..
Centrifugering anvendes også i laboratorier til f.eks. At adskille forbindelser og således adskille deres bestanddele ved forskel i densiteter. Hver gang vi taler om centrifugering, er der en cirkulær bevægelse, der er ensartet, i det mindste et stykke tid.
Have vanddåser
Mange havesprinklere roterer med konstant hastighed, så jorden vandes jævnt..
sport

I for eksempel hammerkastet, som er en olympisk disciplin, drejer atleten en metalkugle med kraft ved hjælp af et stålkabel fastgjort til grebet. Målet er at sende bolden så langt som muligt, men uden at forlade et bestemt område.
Træning løst
En partikel bevæger sig i en omkreds på radius 2m med en konstant hastighed v = 8 m / s mod uret. Oprindeligt var partiklen i r = +2 j m. Beregn:
a) Vinkelhastigheden ω
b) Dens vinkelposition θ (t)
c) Bevægelsesperioden
d) Centripetal acceleration.
e) Partiklens position efter passage af t = π / 4 s
Løsning til
Fra formlen v = Rω følger det, at:
ω = v / R = (8 m / s) / 2m = 4rad ∙ s-1
Løsning b
Idet man tager den positive x-akse som referenceakse, er partiklen indledningsvis ved 90º = π / 2 radianer i forhold til aksen, da udsagnet siger, at startpositionen er +2 j m, det vil sige, at partiklen er på y = 2m, når bevægelsen begynder at følge.
θ = θ (t) = θeller + ωt = π / 2 + 4t
Løsning c
T = 2π / ω = 2π / 4 s = 0,5 π s
Løsning d
a = vto / R = (8 m / s)to / 2 m = 32 m / sto
Løsning e
θ (t) = π / 2 + 4t → θ (π / 4) = π / 2 + 4 ∙ (π / 4) = 3π / 2 radianer
Dette betyder, at partiklen efter dette tidspunkt er i positionen y = -2m j. Det giver mening, fordi t = π / 4 s er halvdelen af perioden, hvorfor partiklen bevægede en 180 ° vinkel mod uret fra sin oprindelige position, og den skal være lige i den modsatte position.
Referencer
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 1. kinematik. Redigeret af Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysik. 2. plads Ed. McGraw Hill.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1. Pearson.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7. Ed. Cengage Learning.
- Zapata, F. Cirkulær bevægelse. Gendannet fra: francesphysics.blogspot.com.



Endnu ingen kommentarer