
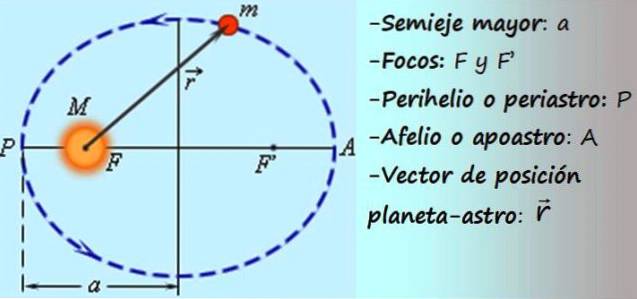
Elliptisk bevægelse
Hvad er elliptisk bevægelse?
I elliptisk bevægelse beskriver mobilen en ellipse, ligesom planeterne gør omkring Solen, og Månen og kunstige satellitter omkring Jorden, for at nævne et par velkendte eksempler..
Den kraft, der giver anledning til denne bevægelse, er tyngdekraften, en central kraft. Disse kræfter er rettet mod (eller fra) et fast punkt O, og deres modul afhænger af afstanden til dette punkt. Hvis r er afstanden og ellerr er enhedsvektoren i radial retning, den centrale kraft F er en vektorfunktion af formen:
F = F (r) ellerr
Med en del matematik kan det vises, at bevægelsen af et objekt under tyngdekraften følger en af disse fire baner: ellipse, omkreds, hyperbola eller parabel.
Karakteristika for den elliptiske bevægelse
Nogle af de vigtigste egenskaber ved elliptisk bevægelse under central styrke er:
-Vinkelmomentet i forhold til O bevares, kaldes L og der beregnes gennem vektorproduktet mellem positions- og hastighedsvektorerne: L = r × mv, hvor m repræsenterer massen af det bevægelige objekt.
-Den elliptiske bane ligger i planet bestemt af vektorerne r Y v.
-Fra bevarelsen af vinkelmoment er den såkaldte lov om områder, som fastslår, at mobilen rejser lige store områder på lige tid.
-Mekanisk energi bevares også i elliptisk bevægelse, hvis der ikke er nogen spredende kræfter.
-Den tid, det tager for mobilen at give en bane, og dens samlede energi afhænger kun af længden "a" af ellipsens halv-store akse..
Forskelle med cirkulær bevægelse
Selvom objektet både i cirkulær og elliptisk bevægelse bevæger sig i en lukket og gentagen sti, dvs. periodisk, er der åbenlyse forskelle mellem en bevægelse og en anden, såsom:
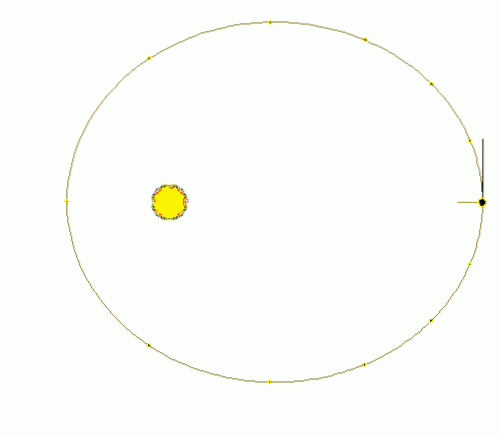
-I cirkulær bevægelse beskriver mobilen en omkreds, hvis radius (afstand til stiens centrum) er konstant, mens den i elliptisk bevægelse beskriver en ellipse, hvor afstanden til stiens centrum er variabel (se figur 1).
-I tilfælde af ensartet cirkulær bevægelse MCU fejer mobilen lige vinkler i lige tid, men i planetarisk elliptisk bevægelse fejes lige områder i lige tid. Dette er loven om områder, også kendt som Keplers anden lov om planetbevægelse..
Vigtige ligninger af planetarisk elliptisk bevægelse
Periode
I elliptisk bevægelse, der stammer fra tyngdekraften, er bevægelsesperioden den tid, det tager for planeten eller satellitten (m) at foretage en elliptisk drejning omkring solen eller jorden (M). Ved anvendelse af energibesparelse følger det, at den er proportional med terningen af længden af ellipsens halv-store akse:

Hvor G er den universelle gravitationskonstant: 6,67 × 10-elleve N ∙ mto/ kgto, M er massen af Solen, Jorden eller objektet, der forårsager interaktionen på m og "a" er længden af den halv-store akse.
Mekanisk energi
Den samlede energi til planeten (m) - Sol (M) -systemet er:

Vinkelmoment
Størrelsen af vinkelmomentet ved et punkt på den elliptiske bane afhænger også af længden af den semi-store akse såvel som af excentriciteten "e", en dimensionsløs parameter, der angiver, hvor flad ellipsen er. Hvis e = 0, bliver ellipsen en cirkel.

Fart
Hastighedens størrelse er givet ved følgende ligning:

Hvor r er afstanden mellem et punkt på banen (planetens placering) og fokus (sol).
Eksempler på elliptisk bevægelse
Planetariske bevægelser
Keplers første lov fastslår, at bevægelsen af planeterne omkring Solen følger en elliptisk sti med Solen i et af brændpunkterne. Nogle kometer, der regelmæssigt besøger jorden, såsom Halleys komet, følger også en elliptisk bevægelse..
Bortset fra denne elliptiske translationelle bevægelse og rotationen omkring deres akse, har planeterne deres egne bevægelser på grund af de komplekse gravitationsinteraktioner med de andre planeter og himmellegemer i solsystemet. På denne måde er de præcessions- og nutationsbevægelser, som Jorden besidder, og som skyldes solens og månens fælles tyngdekraft..
I precession beskriver jordaksen en kegle, når den roterer rundt om aksen vinkelret på planen eller ekliptikken. Og i nutation, som er overlejret på præcession, svinger Jordens akse op og ned i en elliptisk sløjfe hvert 18,6 år. I alt 1385 af disse sløjfer siden 25.767 år, hvilket er perioden med jordens akses nedgang.
En partikel af havvand
I havvand udfører en partikel en elliptisk bevægelse, hvor ellipsen bliver mere og mere fladt med stigende dybde. På den anden side, når vandet er dybt, er partiklernes bevægelse cirkulær.
Hvad der sker er, at når bølgen nærmer sig kysten, vises friktionskræfter takket være dens nærhed til bunden, og denne friktion har tendens til at bremse bevægelsen i den nedre del af banen, mens toppen fortsætter sin bevægelse..
Resultatet er, at omkredsen flader, og effekten forstærkes, når dybden øges..

Elliptisk svingningsform i et fysisk pendul
Et fysisk pendul består af et stift fast stof, der kan svinge i et plan omkring en akse vinkelret på det. Hvis objektet får lov til at bevæge sig frit, kan det beskrive en hvilken som helst vinkel omkring aksen, der forbinder massepunktet med ophængningspunktet, samt rotere omkring det..
Takket være jordens rotation er pendulet i stand til at beskrive baner med omtrent elliptisk form, der er kendt som elliptisk svingningstilstand, der er kendetegnet ved en anden vinkelmoment end 0.
Der er også plantilstand (vinkelmoment 0) og konisk tilstand (anden vinkelmoment end 0), sidstnævnte med en cirkulær sti på et vandret plan.
Elliptiske cykler
De elliptiske bevægelser, der er beskrevet tidligere, forekommer i naturen, men kan også bruges til at fremstille nyttige gadgets, såsom elliptiske cykler, som er meget populære maskiner til aerobic..
De er stationære cykler, der grundlæggende består af et styr og to pedaler, som personen aktiverer ved at skubbe sig selv med sin vægt og beskriver en ellipse med fødderne. Dette er en naturlig bevægelse med lav effekt, som er gavnlig, fordi den bevæger mange muskelgrupper i hele kroppen..
Referencer
- Astronomi for alle. Precession og nutation. Gendannet fra: astronomiaparatodos.com.
- Beregning af hastigheden i elliptiske baner. Gendannet fra: forum.lawebdefisica.com.
- Fowler, Michael. Elliptiske baner: Stier til planeterne. Gendannet fra: galileo.phys.virginia.edu.
- Hernández, J. Undersøgelse af svingningstilstandene i et symmetrisk fysisk pendul ved hjælp af det effektive potentiale. Gendannet fra: scielo.org.co.
- Kittel, C. 1973. Mekanik. Berkeley fysik kursus. Bind 1. Red. Reverté.
- Elliptiske baner under handling af central styrke. Gendannet fra: sc.ehu.es.
- Konservative systemer. Gendannet fra: dfmf.uned.es.Wikipedia. Elliptisk bane. Gendannet fra: en.wikipedia.org.


Endnu ingen kommentarer