
Reynolds nummererer, hvad det er til, hvordan det beregnes, øvelser
Det Reynolds nummer (Rog) er en dimensionsløs numerisk størrelse, der fastslår forholdet mellem de inertiale kræfter og de viskose kræfter i en væske i bevægelse. Træghedskræfter bestemmes af Newtons anden lov og er ansvarlige for den maksimale acceleration af væsken. Viskose kræfter er de kræfter, der modsætter sig væskens bevægelse.
Reynolds-nummeret gælder for enhver form for væskestrøm, såsom strømning i cirkulære eller ikke-cirkulære kanaler, i åbne kanaler og strømning omkring neddykkede kroppe..
Værdien af Reynolds-nummeret afhænger af densiteten, viskositeten, hastigheden af væsken og dimensionerne af den aktuelle vej. En væskes opførsel som en funktion af den mængde energi, der spredes på grund af friktion, vil afhænge af, om strømningen er laminær, turbulent eller mellemliggende. Af denne grund er det nødvendigt at finde en måde at bestemme typen af strømning på.
En måde at bestemme dette på er ved hjælp af eksperimentelle metoder, men de kræver meget præcision i målinger. En anden måde at bestemme strømningstypen på er ved at få Reynolds-nummeret.
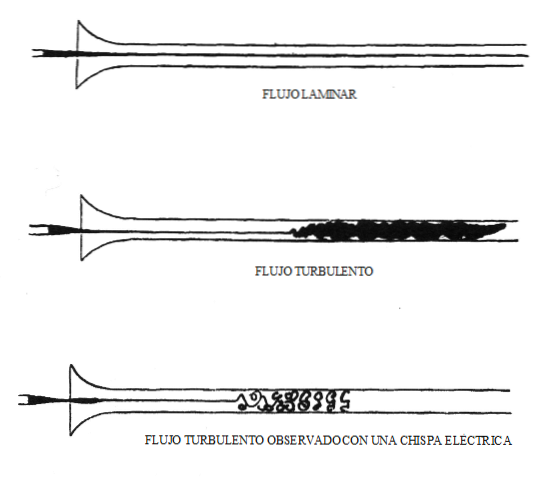
I 1883 opdagede Osborne Reynolds, at hvis værdien af dette dimensionsløse tal er kendt, kan den type strøm, der karakteriserer enhver situation med væskeledning, forudsiges..
Artikelindeks
- 1 Hvad er Reynolds-nummeret til?
- 2 Hvordan beregnes det?
- 3 Løst øvelser
- 3.1 Reynolds-nummer i en cirkulær kanal
- 3.2 Reynolds-nummer i en rektangulær kanal
- 3.3 Reynolds antal af en kugle nedsænket i en væske
- 4 applikationer
- 4.1 Anvendelser i biologi
- 5 Referencer
Hvad er Reynolds-nummeret til?
Reynolds-nummeret bruges til at bestemme en fluids opførsel, det vil sige til at bestemme, om strømmen af en væske er laminær eller turbulent. Strømningen er laminær, når de tyktflydende kræfter, der modsætter sig væskens bevægelse, er dem, der dominerer, og væsken bevæger sig med tilstrækkelig lille hastighed og i en retlinet bane.
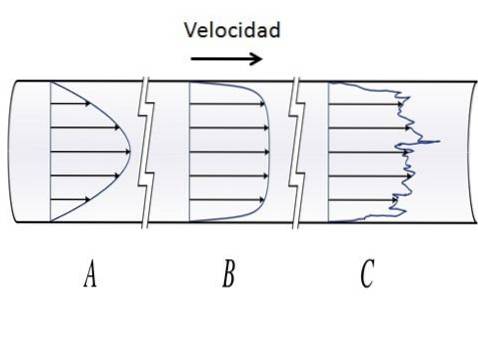
Væsken med laminær strøm opfører sig som om det var uendelige lag, der glider over hinanden på en ordnet måde uden blanding. I cirkulære kanaler har den laminære strømning en parabolisk hastighedsprofil med maksimale værdier i midten af kanalen og minimumsværdier i lagene nær kanaloverfladen. Værdien af Reynolds-tallet i laminær strømning er Rog<2000.
Strømmen er turbulent, når inerti-kræfterne er dominerende, og væsken bevæger sig med svingende hastighedsændringer og uregelmæssige baner. Turbulent strømning er meget ustabil og udviser momentumoverførsler mellem væskepartikler.
Når væsken cirkulerer i en cirkulær ledning med turbulent strømning, skærer væskelagene hinanden og danner hvirvler, og deres bevægelse har tendens til at være kaotisk. Reynolds-talværdien for turbulent flow i en cirkulær kanal er Rog > 4000.
Overgangen mellem laminær strømning og turbulent strømning forekommer for Reynolds-talværdier mellem 2000 Y 4000.
Hvordan beregnes det?
Ligningen, der bruges til at beregne Reynolds-tallet i en kanal med cirkulært tværsnit, er:
Rog = ρVD / η
ρ = Væsketæthed (kg / m3)
V = Flowhastighed (m3/ s)
D = Karakteristisk lineær dimension af væskestien, som for tilfældet med den cirkulære kanal repræsenterer diameteren.
η = dynamisk viskositet af væsken (Pa.s)
Forholdet mellem viskositet og densitet er defineret som kinematisk viskositet v = η / ρ, og dens enhed er mto/ s.
Ligningen af Reynolds-tallet som en funktion af kinematisk viskositet er:
Rog = VD / v
I kanaler og kanaler med ikke-cirkulære tværsnit er den karakteristiske dimension kendt som hydraulisk diameter DH y repræsenterer en generaliseret dimension af væskestien.
Den generaliserede ligning til beregning af Reynolds-tallet i kanaler med ikke-cirkulære tværsnit er:
Rog = ρV 'DH / η
V '= Gennemsnitlig strømningshastighed =GOES
Hydraulisk diameter DH etablerer forholdet mellem området TIL af strømningsstrømstværsnit og befugtet omkreds PM .
DH = 4A / PM
Den våde omkreds PM er summen af længderne af kanalens eller kanalens vægge, der er i kontakt med væsken.
Du kan også beregne Reynolds-antallet af en væske, der omgiver en genstand. For eksempel en kugle nedsænket i en væske, der bevæger sig med hastighed V. Kuglen oplever en trækkraft FR defineret af Stokes ligningen.
FR = 6πRVη
R = kuglens radius
Reynolds-nummeret på en kugle med hastighed V nedsænket i en væske er:
Rog = ρV R / η
Rog<1 cuando el flujo es laminar y Rog > 1 når flowet er turbulent.
Løst øvelser
Følgende er tre Reynolds antal applikationsøvelser: Cirkulær kanal, rektangulær kanal og kugle nedsænket i en væske.
Reynolds nummer i en cirkulær kanal
Beregn Reynolds-antallet af propylenglycol a 20 °C i en cirkulær kanal med diameter 0,5 cm. Strømningshastigheden er 0,15 m3/ s. Hvad er typen af flow?
D =0,5 cm = 5.10-3m (karakteristisk dimension)
Væsketæthed er ρ = 1.036 g / cm3= 1036 kg / m3
Viskositeten af væsken er η = 0,042 Pa s = 0,042 kg / m.s
Flowhastighed er V = 0,15 m3/ s
Reynolds-talligningen bruges i en cirkulær kanal.
Rog =ρDU/η
Rog = (1036 kg / m3x0.15m3/ s x 5.10-3m) /(0,042 kg / m.s) = 18,5
Strømningen er laminær, fordi værdien af Reynolds-tallet er lav i forhold til forholdet Rog<2000
Reynolds nummer i en rektangulær kanal
Bestem typen af ethanolstrøm, der flyder med en hastighed på 25 ml / min i et rektangulært rør. Dimensionerne på det rektangulære afsnit er 0,5 cm og 0,8 cm.
Massefylde ρ = 789 kg / m3
Dynamisk viskositet η = 1.074 mPa s = 1.074,10-3 kg / m.s
Bestem først den gennemsnitlige strømningshastighed.
V ' =GOES
V = 25 ml / min = 4.16.10-7m3/ s
Tværsnittet er rektangulært, hvis sider er 0,005m og 0,008m. Tværsnitsarealet er A = 0,005m x0,008m = 4,10-5mto
V ' = (4.16.10-7m3/ s) / (4.10-5mto) = 1,04 × 10-toFrk
Den befugtede omkreds er summen af siderne af rektanglet.
PM=0,013m
Den hydrauliske diameter er DH = 4A / PM
DH = 4 × 4,10-5mto/ 0,013m
DH= 1.23.10-tom
Reynolds-nummeret fås fra ligningen Rog = ρV 'DH / η
Rog = (789 kg / m3x1,04 × 10-tom / s x1.23.10-tom) / 1.074,10-3 kg / m.s
Rog = 93974
Strømmen er turbulent, fordi Reynolds-tallet er meget stort (Rog> 2000)
Reynolds nummer af en kugle nedsænket i en væske
En sfærisk latex polystyrenpartikel, hvis radius er R= 2000 nm kastes lodret i vandet med en indledende størrelseshastighed V0= 10 m / s. Bestem Reynolds-antallet af partikler nedsænket i vandet
Partikeltæthed ρ = 1,04 g / cm3 = 1040 kg / m3
R= 2000 nm = 0,000002 m
Vandtæthed ρag= 1000 kg / m3
Viskositet η =0,001 kg / (m s)
Reynolds-nummeret opnås ved hjælp af ligningen Rog = ρV R / η
Rog = (1000 kg / m3x10 m / s x 0,000002m) / 0,001 kg / (m s)
Rog = 20
Reynolds-tallet er 20. Strømmen er turbulent.
Ansøgninger
Reynolds-nummeret spiller en vigtig rolle i væskemekanik og varmeoverførsel, fordi det er en af de vigtigste parametre, der karakteriserer en væske. Nogle af dens applikationer er nævnt nedenfor.
1-Det bruges til at simulere bevægelsen af organismer, der bevæger sig på flydende overflader såsom: bakterier suspenderet i vand, der svømmer gennem væsken og frembringer tilfældig omrøring.
2-Det har praktiske anvendelser i strømmen af rør og i væskecirkulationskanaler, begrænsede strømme, især i porøse medier.
3-I suspensionerne af faste partikler nedsænket i en væske og i emulsioner.
4-Reynolds-nummeret anvendes i vindtunneltest for at undersøge de aerodynamiske egenskaber af forskellige overflader, især i tilfælde af flyvninger.
5-Det bruges til at modellere bevægelse af insekter i luften.
6-Udformningen af kemiske reaktorer kræver brug af Reynolds-nummeret til at vælge flowmodellen under hensyntagen til hovedtab, energiforbrug og området for varmetransmission..
7-I forudsigelsen af varmeoverførslen af elektroniske komponenter (1).
8-I løbet af vanding af haver og frugtplantager, hvor det er nødvendigt at kende strømmen af vand, der kommer ud af rørene. For at få disse oplysninger bestemmes det hydrauliske hovedtab, som er relateret til den friktion, der findes mellem vandet og rørvæggene. Trykfaldet beregnes, når Reynolds-nummeret er opnået.

Anvendelser i biologi
I biologi kræver undersøgelsen af levende organismeres bevægelse gennem vand eller i væsker med egenskaber svarende til vand at opnå Reynolds-nummeret, hvilket vil afhænge af størrelsen på organismerne og den hastighed, hvormed de fortrænges.
Bakterier og encellede organismer har et meget lavt Reynolds-antal (Rog<<1Strømmen har følgelig en laminær hastighedsprofil med en overvægt af viskose kræfter.
Organismer med en størrelse tæt på myrer (op til 1 cm) har et Reynolds-nummer i størrelsesordenen 1, hvilket svarer til overgangsregimet, hvor de inertiakræfter, der virker på organismen, er lige så vigtige som væskens viskose kræfter.
I større organismer som mennesker er antallet af Reynolds meget stort (Rog>> 1).
Referencer
- Anvendelse af lav-Reynolds antal turbulente strømningsmodeller til forudsigelse af elektronisk komponent varmeoverførsel. Rodgers, P og Eveloy, V. NV: s.n., 2004, IEEE, bind 1, s. 495-503.
- Mott, R L. Anvendt væskemekanik. Berkeley, CA: Pearson Prentice Hall, 2006, bind I.
- Collieu, A M og Powney, D J. Materialers mekaniske og termiske egenskaber. New YorK: Crane Russak, 1973.
- Kay, J M og Nedderman, R M. En introduktion til væskemekanik og varmeoverførsel. New York: Cambridge Universitty Press, 1974.
- Happel, J og Brenner, H. Væskemekanik og transportprocesser. Hingham, MA: MartinusS Nijhoff Publishers, 1983.



Endnu ingen kommentarer