
Irrationelle tal historie, egenskaber, klassificering, eksempler
Det irrationelle tal er dem, hvis decimale udtryk har uendelige tal uden et gentaget mønster, derfor kan de ikke opnås ved at gøre kvotienten mellem to heltal.
Blandt de bedst kendte irrationelle tal er:

Blandt dem er π (pi) uden tvivl den mest velkendte, men der er mange flere. Alle hører til sættet med reelle tal, som er det numeriske sæt, der grupperer rationelle og irrationelle tal..
Ellipsen i figur 1 indikerer, at decimalerne fortsætter på ubestemt tid, hvad der sker er, at rummet i almindelige regnemaskiner kun tillader visning af et par få.
Hvis vi ser nøje, når vi laver kvotienten mellem to hele tal, får vi en decimal med begrænsede tal eller, hvis ikke, med uendelige tal, hvor en eller flere gentages. Nå, dette sker ikke med irrationelle tal..
Artikelindeks
- 1 Historie af irrationelle tal
- 2 Egenskaber for irrationelle tal
- 3 Placering af et irrationelt tal på den rigtige linje
- 4 Klassificering af irrationelle tal
- 4.1 Algebraiske tal
- 4.2 Transcendente tal
- 5 Motion
- 5.1 Svar
- 6 Referencer
Historien om irrationelle tal
Den store gamle matematiker Pythagoras, født 582 f.Kr. i Samos, Grækenland, grundlagde Pythagoras tankeskole og opdagede den berømte sætning, der bærer hans navn. Vi har det her nede til venstre (måske vidste babylonierne det allerede længe før).
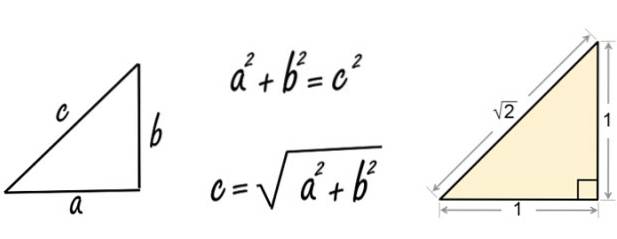
Når Pythagoras (eller sandsynligvis en discipel af ham) anvendte sætningen på en højre trekant med sider lig med 1, fandt han det irrationelle tal √2.
Han gjorde det på denne måde:
c = √1to + 1to = √1 + 1 = √2
Og straks indså han, at dette nye tal ikke kom fra kvotienten mellem to andre naturlige tal, som var dem, der var kendt på det tidspunkt.
Derfor kaldte han det irrationel, og opdagelsen forårsagede stor angst og forvirring blandt pythagoreerne.
Egenskaber for irrationelle tal
-Sættet med alle irrationelle tal er betegnet med bogstavet I og undertiden som Q * eller QC. Foreningen mellem de irrationelle tal I eller Q * og de rationelle tal Q giver anledning til sættet med reelle tal R.
-Med irrationelle tal kan de kendte aritmetiske operationer udføres: addition, subtraktion, multiplikation, division, empowerment og mere.
-Division med 0 er heller ikke defineret mellem irrationelle tal.
-Summen og produktet mellem irrationelle tal er ikke nødvendigvis et andet irrationelt tal. For eksempel:
√2 x √8 = √16 = 4
Og 4 er ikke et irrationelt tal.
-Imidlertid resulterer summen af et rationelt tal plus et irrationelt tal i et irrationelt. På denne måde:
1 + √2 = 2.41421356237 ...
-Produktet af et andet rationelt tal end 0 med et irrationelt tal er også irrationelt. Lad os se på dette eksempel:
2 x √2 = 2.828427125 ...
-Det omvendte af en irrationel resulterer i et andet irrationelt tal. Lad os prøve nogle:
1 / √2 = 0,707106781…
1 / √3 = 0.577350269 ...
Disse tal er interessante, fordi de også er værdierne for nogle trigonometriske forhold mellem kendte vinkler. De fleste af de trigonometriske forhold er irrationelle tal, men der er undtagelser, såsom sin 30º = 0,5 = ½, hvilket er rationelt.
-Derudover er kommutative og associerende egenskaber opfyldt. Hvis a og b er to irrationelle tal, betyder det at:
a + b = b + a.
Og hvis c er et andet irrationelt tal, så:
(a + b) + c = a + (b + c).
-Den fordelende egenskab ved multiplikation med hensyn til addition er en anden velkendt egenskab, der også holder for irrationelle tal. I dette tilfælde:
a. (b + c) = a.b + a.c.
-En irrationel a har sin modsatte: -a. Når de lægges sammen, er resultatet 0:
a + (- a) = 0
-Mellem to forskellige rationelle er der mindst et irrationelt tal.
Placering af et irrationelt tal på den rigtige linje
Den rigtige linje er en vandret linje, hvor de reelle tal er placeret, hvor irrationelle er en vigtig del.
For at finde et irrationelt tal på den rigtige linje i geometrisk form kan vi bruge Pythagoras sætning, en lineal og et kompas.
Som et eksempel skal vi lokalisere √5 på den rigtige linje, hvor vi tegner en ret trekant med sider x = 2 Y y = 1, som billedet viser:
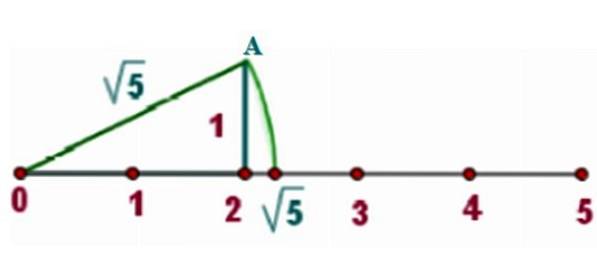
Ved Pythagoras sætning er hypotenusen af en sådan trekant:
c = √2to + 1to = √4 + 1 = √5
Nu er kompasset placeret med punktet 0, hvor en af hjørnerne i den højre trekant også er. Kompasblyantens punkt skal være ved hjørne A.
En cirkelbue er tegnet, der skærer til den rigtige linje. Da afstanden mellem centrum af omkredsen og ethvert punkt på den er radius, som er lig med √5, er skæringspunktet også langt √5 fra centrum.
Fra grafen kan det ses, at √5 er mellem 2 og 2,5. En lommeregner giver os den omtrentlige værdi af:
√5 = 2.236068
Og så ved at opbygge en trekant med de relevante sider kan andre irrationelle findes, såsom √7 og andre.
Klassificering af irrationelle tal
Irrationelle tal er klassificeret i to grupper:
-Algebraisk
-Transcendent eller transcendental
Algebraiske tal
Algebraiske tal, som måske eller måske ikke er irrationelle, er løsninger på polynomiske ligninger, hvis generelle form er:
tiln xn + tiln-1xn-1 + tiln-2xn-2 +…. + a1x + aeller = 0
Et eksempel på en polynomligning er en kvadratisk ligning som denne:
x3 - 2x = 0
Det er let at vise, at det irrationelle tal √2 er en af løsningerne i denne ligning.
Transcendente tal
På den anden side opstår de transcendente tal, selvom de er irrationelle, aldrig som en løsning af en polynomligning.
De transcendente tal, der findes hyppigst i anvendt matematik, er π på grund af dets forhold til omkredsen og antallet e, eller Eulers nummer, som er basen for naturlige logaritmer..
Dyrke motion
En grå firkant placeres på en sort firkant i den position, der er angivet i figuren. Overfladen på den sorte firkant er kendt for at være 64 cmto. Hvor meget er længden af begge firkanter?

Svar
Arealet af en firkant med side L er:
A = L.to
Da den sorte firkant er 64 cmto areal, skal siden være 8 cm.
Denne måling er den samme som diagonalen af den grå firkant. Ved at anvende Pythagoras sætning på denne diagonal og huske at siderne af en firkant måler det samme, vil vi have:
8to = Lgto + Lgto
Hvor Lg er siden af den grå firkant.
Derfor: 2Lgto = 8to
Anvendelse af kvadratrod på begge sider af ligestillingen:
Lg = (8 / √2) cm
Referencer
- Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
- Figuera, J. 2000. Matematik 9.. Karakter. CO-BO udgaver.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Uddannelsesportal. Irrationelle tal og deres egenskaber. Gendannet fra: portaleducativo.net.
- Wikipedia. Irrationelle tal. Gendannet fra: es.wikipedia.org.



Endnu ingen kommentarer