
Virkelige tal historie, eksempler, egenskaber, operationer

Det reelle tal de udgør det numeriske sæt, der inkluderer de naturlige tal, heltalene, det rationelle og det irrationelle. De er betegnet med symbolet ℝ eller simpelthen R og omfanget inden for videnskab, teknik og økonomi er sådan, at når man taler om "antal", er det næsten taget for givet, at det er et reelt tal.
Reelle tal er blevet brugt siden oldtiden, skønt de ikke fik det navn. Allerede fra det tidspunkt, hvor Pythagoras udviklede sin berømte sætning, opstod der tal, der ikke kunne opnås som kvoter af naturlige tal eller heltal.
Eksempler på tal er √2, √3 og π. Disse numre kaldes irrationel, i modsætning til rationelle tal, der kommer fra heltal. Det var derfor nødvendigt et numerisk sæt, der omfatter begge klasser af tal..
Udtrykket "reelt tal" blev skabt af den store matematiker René Descartes (1596-1650) for at skelne mellem de to slags rødder, der kan opstå ved at løse en polynomligning.
Nogle af disse rødder kan endda være rødder af negative tal, Descartes kaldte disse "imaginære tal", og dem der ikke var, var reelle tal.
Benævnelsen fortsatte over tid, hvilket gav anledning til to store numeriske sæt: reelle tal og komplekse tal, et større sæt, der inkluderer reelle tal, imaginære tal og dem, der er del reelle og del imaginære..
Udviklingen af reelle tal fortsatte sin gang, indtil matematikeren Richard Dedekind (1831-1936) i 1872 formelt definerede sættet af reelle tal gennem den såkaldte nedskæringer af Dedekind. Syntese af hans arbejde blev offentliggjort i en artikel, der så lyset samme år.
Artikelindeks
- 1 Eksempler på reelle tal
- 1.1 Repræsentation af reelle tal på den rigtige linje
- 2 Egenskaber for reelle tal
- 3 Operationer med reelle tal
- 4 applikationer
- 5 Øvelse løst
- 5.1 Øvelse 1
- 6 Referencer
Eksempler på reelle tal
Tabellen nedenfor viser eksempler på reelle tal. Dette sæt har som delmængder de naturlige tal, heltalene, det rationelle og det irrationelle. Ethvert antal af disse sæt er i sig selv et reelt tal.
Derfor 0, negativer, positive, brøker og decimaler er reelle tal.

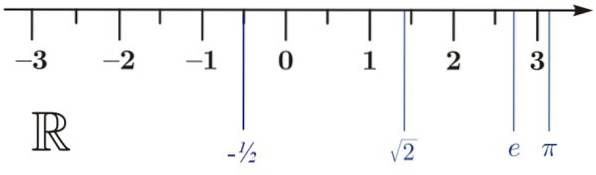
Repræsentation af reelle tal på den rigtige linje
Reelle tal kan vises på den rigtige linje R, som billedet viser. Det er ikke nødvendigt, at 0 altid er til stede, men det er praktisk at vide, at til venstre er de negative realer og til højre de positive. Derfor er det et glimrende referencepunkt.
På den rigtige linje tages en skala, hvor heltalene findes:… 3, -2, -1, 1, 2, 3…. Pilen indikerer, at linjen strækker sig til uendelig. Men det er ikke alt, i ethvert betragtet interval, vil vi også altid finde uendelige reelle tal.
De reelle tal er repræsenteret i rækkefølge. Til at begynde med er der rækkefølgen af heltalene, hvor de positive altid er større end 0, mens de negative er mindre..
Denne ordre holdes inden for de reelle tal. Følgende uligheder er vist som et eksempel:
a) -1/2 < √2
b) e < π
c) π> -1/2
Egenskaber for reelle tal
-Reelle tal inkluderer naturlige tal, heltal, rationelle tal og irrationelle tal..
-Den kommutative egenskab ved tilføjelsen er opfyldt: rækkefølgen af tilføjelserne ændrer ikke summen. Hvis a og b er to reelle tal, er det altid sandt at:
a + b = b + a
-0 er det neutrale element i summen: a + 0 = a
-For summen er den associerede ejendom opfyldt. Hvis a, b og c er reelle tal: (a + b) + c = a + (b + c).
-Det modsatte af et reelt tal til er -a.
-Subtraktion er defineret som summen af det modsatte: a - b = a + (-b).
-Produktets kommutative egenskab er opfyldt: rækkefølgen af faktorer ændrer ikke produktet: a.b = b.a
-I produktet anvendes den associerende egenskab også: (a.b) .c = a. (B.c)
-1 er det neutrale element i multiplikationen: a.1 = a
-Den fordelende egenskab ved multiplikation med hensyn til tilføjelse er gyldig: a. (b + c) = a.b + a.c
-Opdeling med 0 er udefineret.
-Ethvert reelt tal a, undtagen 0, har en multiplikativ invers af-1 sådan at a.a-1 = 1.
-Hvis a er et reelt tal: a0 = 1 og a1 = a.
-Den absolutte værdi eller modul for et reelt tal er afstanden mellem tallet og 0.
Operationer med reelle tal
Med de reelle tal kan du udføre de operationer, der udføres med de andre numeriske sæt, herunder addition, subtraktion, multiplikation, division, empowerment, radication, logaritmer og mere.
Som altid er division med 0 ikke defineret, hverken negative logaritmer af tal eller 0, selvom det er rigtigt, at log 1 = 0, og at logaritmer med tal mellem 0 og 1 er negative.
Ansøgninger
Anvendelsen af reelle tal på alle slags situationer er ekstremt varieret. Reelle tal fremstår som svar på mange problemer inden for eksakt videnskab, datalogi, teknik, økonomi og samfundsvidenskab..
Alle slags størrelser og størrelser som afstande, tider, kræfter, lydintensitet, penge og mange flere har deres udtryk i reelle tal.
Overførsel af telefonsignaler, billedet og lyden af en video, temperaturen i et klimaanlæg, et varmelegeme eller et køleskab kan styres digitalt, hvilket betyder at omdanne fysiske størrelser til numeriske sekvenser.
Det samme sker, når du foretager en banktransaktion over Internettet eller konsulterer instant messaging. De reelle tal er overalt.
Træning løst
Vi vil med øvelser se, hvordan disse tal fungerer i almindelige situationer, som vi støder på dagligt..
Øvelse 1
Postkontoret accepterer kun pakker, for hvilke længden plus omkredsmålingen ikke overstiger 108 tommer. For at den viste pakke kan accepteres, skal det derfor være opfyldt, at:
L + 2 (x + y) ≤ 108
a) Kommer en pakke, der måler 6 tommer bred, 8 tommer høj og 5 fod lang, igennem??
b) Hvad med en, der måler 2 x 2 x 4 fod3?
c) Hvad er den højeste acceptable højde for en pakke, hvis bund er firkantet og måler 9 x 9 tommerto?
Svar til
L = 5 fod = 60 tommer
x = 6 tommer
y = 8 tommer
Operationen, der skal løses, er:
L + 2 (x + y) = 60 + 2 (6 + 8) tommer = 60 + 2 x 14 tommer = 60 + 28 tommer = 88 tommer
Pakken accepteres.
Svar b
Dimensionerne på denne pakke er mindre end pakke a), så de formår begge at passere.
Svar c
I denne pakke:
x = L = 9 tommer
Det skal opfyldes, at:
9+ 2 (9 + y) ≤ 108
27 + 2y ≤ 108
2 år ≤ 81
og ≤ 40,5 tommer
Referencer
- Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
- Diego, A. Reelle tal og deres egenskaber. Gendannet fra: matematica.uns.edu.ar.
- Figuera, J. 2000. Matematik 9.. Karakter. CO-BO udgaver.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Stewart, J. 2006. Precalculus: Matematik til beregning. 5. plads Udgave. Cengage læring.



Endnu ingen kommentarer