
Orthohedronformler, areal, volumen, diagonal, eksempler
Det orthoeder Det er en volumetrisk eller tredimensionel geometrisk figur, der er kendetegnet ved at have seks rektangulære flader, så de modsatte flader er i parallelle plan og er identiske eller kongruente rektangler. På den anden side er ansigterne, der støder op til et givet ansigt, i plan vinkelret på det oprindelige ansigt..
Det kan også overvejes orthoeder som et ortogonalt prisme med en rektangulær base, hvori dihedrale vinkler dannet af flyene med to flader, der støder op til en fælles kant, måler de 90º. Den tovinklede vinkel mellem to flader måles på krydset mellem ansigterne med et vinkelret plan, der er fælles for dem.
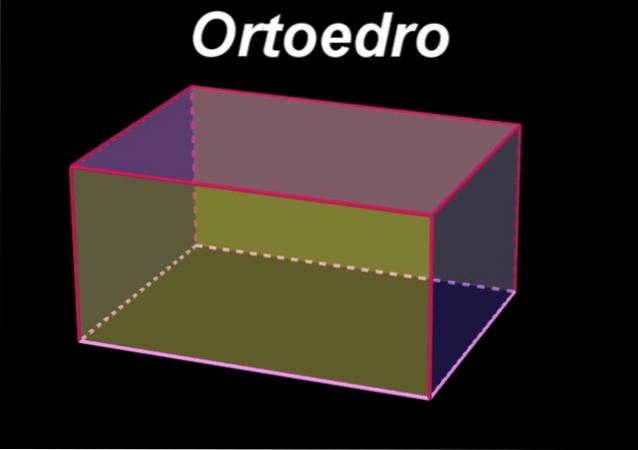
Ligeledes er ortohedronen en rektangel parallelepiped, da dette er, hvordan parallelepiped defineres som den volumetriske figur af seks flader, som er parallelle to og to.
I enhver parallelepiped er ansigterne parallelogrammer, men i den rektangulære parallelepiped skal ansigterne være rektangulære.
Artikelindeks
- 1 Dele af ortohedronet
- 2 Orthohedronformler
- 2.1 Område
- 2.2 Volumen
- 2.3 Indvendig diagonal
- 3 eksempler
- 3.1 - Eksempel 1
- 3.2 - Øvelse 2
- 4 Referencer
Dele af ortohedronen
Delene af en polyhedron, såsom orthoederet, De er:
-Kanter
-Hjørner
-Ansigter
Vinklen mellem to kanter på den ene flade af orthoederet falder sammen med den tovinklede vinkel dannet af dens andre to flader ved siden af hver af kanterne og danner en ret vinkel. Følgende billede præciserer hvert koncept:
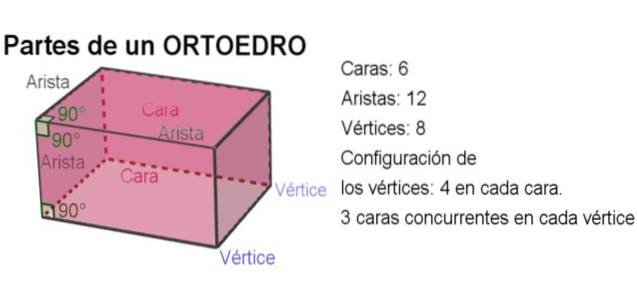
-I alt har en ortohedron 6 ansigter, 12 kanter og 8 hjørner..
-Vinklen mellem to kanter er en ret vinkel.
-Den tovinklede vinkel mellem to ansigter er også rigtig.
-I hvert ansigt er der fire hjørner og i hvert toppunkt tre indbyrdes ortogonale ansigter stemmer overens.
Orthohedron formler
Areal
Overfladen eller arealet af en orthoeder er summen af områderne i deres ansigter.
Hvis de tre kanter, der mødes ved et toppunkt, har målene a, b og c, som vist i figur 3, har frontfladen areal c⋅b og bundfladen har også areal c⋅b.
Så har de to sideflader areal a⋅b hver. Og endelig har gulv- og loftsfladerne areal F.Kr. hver.
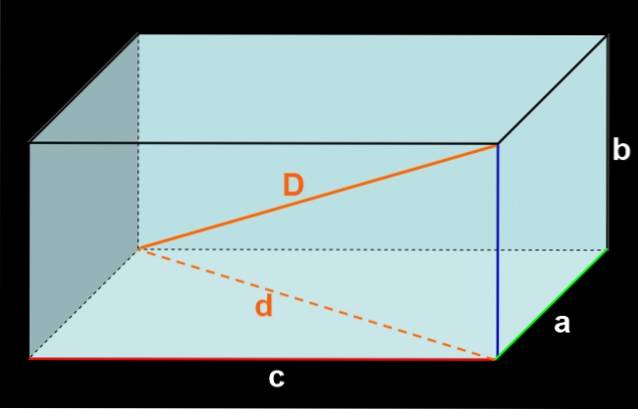
Tilføjelse af arealet af alle ansigter giver:
A = 2⋅c⋅b + 2⋅a⋅b + 2⋅a⋅c
At tage en fælles faktor og bestille ordene:
A = 2⋅ (a⋅b + b⋅c + c⋅a)
Bind
Hvis orthohedronet betragtes som et prisme, beregnes dets volumen som følger:
Volumen = Areal af prisme bunden x prisme højde
I dette tilfælde tages gulvet af dimensioner som den rektangulære bund c Y til, så er basisområdet c⋅a.
Højden er angivet af længden b fra ortogonale kanter til sideflader til Y c.
Multiplicere basisarealet (F.Kr.) efter højde b du har lydstyrken V af ortohedronen:
V = a⋅b⋅c
Indvendig diagonal
I en orthoeder er der to slags diagonaler: de eksterne diagonaler og de indre diagonaler.
De ydre diagonaler er på de rektangulære ansigter, mens de indre diagonaler er de segmenter, der forbinder to modsatte hjørner, forstået af modsatte hjørner dem, der ikke deler nogen kant.
I en orthoeder er der fire indre diagonaler, alle lige store. Længden af de indre diagonaler kan opnås ved at anvende Pythagoras sætning til rigtige trekanter.
Længden d af den udvendige diagonal af ortohedrons gulvflade opfylder det pythagoriske forhold:
dto = ato + cto
Tilsvarende opfylder den indvendige diagonal af mål D det pythagoriske forhold:
Dto = dto + bto.
Kombination af de to tidligere udtryk, vi har:
Dto = ato + cto + bto.
Endelig er længden af en hvilken som helst af de indre diagonaler i orthoederet givet ved følgende formel:
D = √ (ato + bto + cto ).
Eksempler
- Eksempel 1
En murere bygger en tank i form af en orthoeder, hvis indvendige mål er: 6 m x 4 m i bunden og 2 m i højden. Det spørger:
a) Bestem tankens indvendige overflade, hvis den er helt åben øverst.
b) Beregn volumen af tankens indre rum.
c) Find længden af en indvendig diagonal.
d) Hvad er tankens kapacitet i liter?
Løsning til
Vi tager dimensionerne af den rektangulære bund a = 4 m og c = 6 m og højden som b = 2 m
Området for en ortohedron med de givne dimensioner er givet ved følgende forhold:
A = 2⋅ (a⋅b + b⋅c + c⋅a) = 2⋅ (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)
Nemlig:
A = 2⋅ (8 mto + 12 mto + 24 mto) = 2⋅ (44 mto) = 88 mto
Det forrige resultat er arealet af den lukkede ortohedron med de givne dimensioner, men da det er en tank, der er helt afdækket i sin øvre del, for at opnå overfladen af tankens indvendige vægge, området for det manglende låg skal trækkes fra, hvilket er:
c⋅a = 6 m ⋅ 4 m = 24 mto.
Endelig vil tankens indvendige overflade være: S = 88 mto - 24 mto = 64 mto.
Løsning b
Tankens indre volumen er angivet ved volumenet af en orthoeder af tankens indre dimensioner:
V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m3.
Løsning c
Den indvendige diagonal af en oktaeder med dimensionerne af tankens indre har en længde D givet af:
√ (tilto + bto + cto ) = √ ((4 m)to + (2 m)to + (6 m)to )
Vi udfører de angivne operationer:
D = √ (16 mto + 4 mto + 36 mto ) = √ (56 mto) = 2√ (14) m = 7,48 m.
Løsning d
For at beregne tankens kapacitet i liter er det nødvendigt at vide, at volumenet af en kubik decimeter er lig med kapaciteten på en liter. Det var tidligere beregnet i volumen i kubikmeter, men det skal omdannes til kubikcentimeter og derefter til liter:
V = 48 m3 = 48 (10 dm)3 = 4.800 dm3 = 4.800 l
- Øvelse 2
Et glasakvarium har en kubisk form med en side på 25 cm. Bestem området i mto, volumen i liter og længden af en indvendig diagonal i cm.
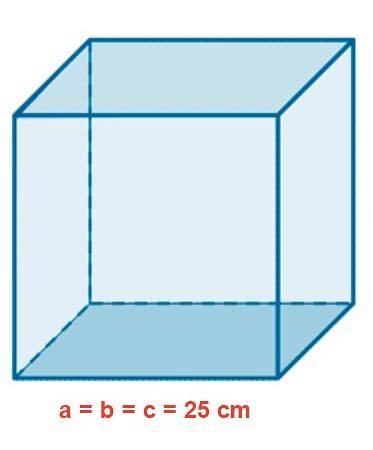
Opløsning
Arealet beregnes ved hjælp af den samme orthoederformel, men under hensyntagen til, at alle dimensionerne er identiske:
A = 2⋅ (3 a⋅a) = 6⋅ ato = 6⋅ (25 cm)to = 1.250 cmto
Kubens volumen er givet af:
V = a3 = (25 cm)3 = 15,625 cm3 = 15,625 (0,1 dm)3 = 15.625 dm3 = 15,625 l.
Længden D på den indvendige diagonal er:
D = √ (3ato) = 25√ (3) cm = 43,30 cm.
Referencer
- Arias J. GeoGebra: Prisme. Gendannet fra: youtube.com.
- Calculus.cc. Øvelser og løste problemer i områder og volumener. Gendannet fra: calculo.cc.
- Salvador R. Pyramid + ortohedron med GEOGEBRA (IHM). Gendannet fra: youtube.com
- Weisstein, Eric. "Orthohedron". MathWorld. Wolfram Research.
- Wikipedia. Orthohedron Gendannet fra: es.wikipedia.com


Endnu ingen kommentarer