Hældning af en linjeformel og ligninger, repræsentation, eksempler

Det hældning af en linje er tangenten for vinklen θ, som linjen dannes med den vandrette akse, som ved konvention måles mod uret. Hældningen på en hvilken som helst linje er altid konstant, og det er derfor en af ​​dens mest væsentlige egenskaber..

For at beregne det skal du kende to punkter på linjen, hvis koordinater er (x₁,Y₁) og (x_to,Y_to). Et segment, der hører til linjen, trækkes mellem begge punkter, og derefter tegnes de segmenter, der repræsenterer afstanden mellem x.₁ og x_to, og mellem og₁ og og_to, som i nedenstående figur.

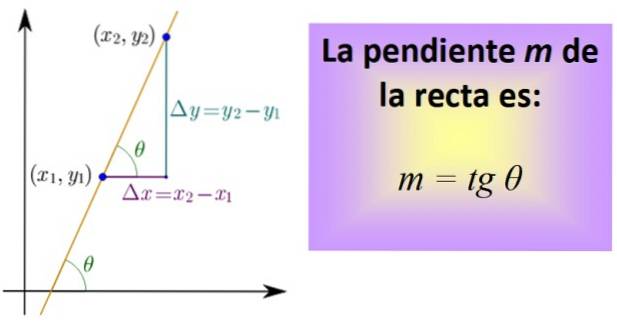
De tre segmenter udgør en højre trekant, hvis ben er: Δx = x_to - x₁  y Δy = y_to - Y₁. De svarer henholdsvis til en vandret og en lodret forskydning..

Nu definerer vi et kvotient, kaldet tangent for vinklen θ og forkortet tg θ, hvilket er nøjagtigt hældningen m af den lige:

m = tg θ = Δy / Δx

Bemærk, at for en linje forbliver denne vinkel konstant, uanset hvilke punkter der tages for at beregne dens tangens. Under alle omstændigheder giver denne værdi os et mål for, hvor stejl linjen er.

Gennem koordinaterne for de valgte punkter er formlen for hældningen:

m = (y - y₁ ) / (x_to - x₁)

Artikelindeks

• 1 Grafisk repræsentation
• 2 Typer af hældning
• 3 Hvordan beregner man hældningen på en linje?
• 4 Løst øvelser
  • 4.1 - Øvelse 1
  • 4.2 - Øvelse 2
• 5 eksempler
  • 5.1 Eksempel 1
  • 5.2 Eksempel 2
• 6 Referencer

Grafisk repræsentation

Nedenfor har vi flere situationer, hvor hældningsbegrebet er relevant. Dens værdi kan let beregnes ved at måle den respektive lodrette og vandrette forskydning og derefter gøre kvotienten angivet i begyndelsen.

Dette giver os en idé om ujævnheder eller tilbagegang i en eller anden struktur, såsom en rampe, et tag eller en vej:

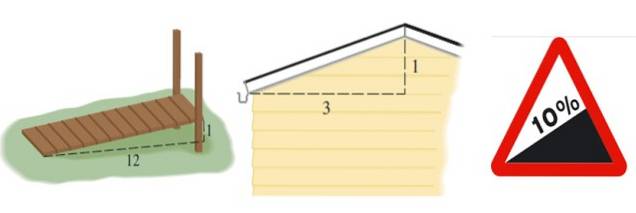
Hældningen på rampen vist i figur 2 til venstre er m = 1/12, tagets er m = 1/3, og vejens er udtrykt i procent. En procentdel på 10% betyder, at for hver 100 meter, der bevæger sig vandret, opnås 10 meter i højden:

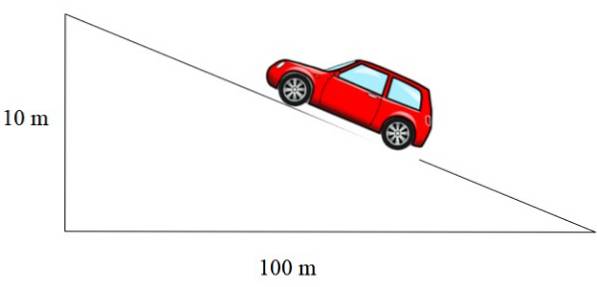
I dette tilfælde er hældningen 10/100 = 0,1, hvilket udtrykt i procent svarer til 10%..

Hældningstyper

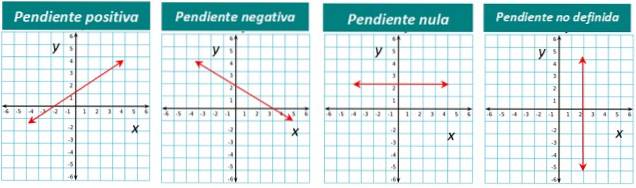
Hældningen på en linje kan være positiv, negativ eller nul. For eksempel har linjen vist i figur 1 en positiv hældning. Vi sætter pris på det med det samme, fordi vi ser, at linjen "stiger", hvis vi ser den fra venstre mod højre.

Hvis linjen falder ned fra venstre mod højre, er dens hældning negativ. Og når en linje er vandret, er hældningen nul.

Endelig er hældningen ikke defineret for lodrette linjer.

Den grafiske repræsentation af hver type er nedenfor:

Hvordan beregner man hældningen på en linje?

Beregning af hældningen er meget enkel, du skal bare finde den lodrette forskydning og den vandrette forskydning og derefter lave kvotienten mellem begge.

Når vi har tegnet linjen i det kartesiske plan, findes disse forskydninger ved at vælge et hvilket som helst to punkter på linjen P₁ Og s_to, bestemmelse af dets koordinater og anvendelse af definitionen i starten:

m = (y - y₁ ) / (x_to - x₁ )

Da hældningsværdien er uafhængig af valget af P₁ Og s_to , vi vælger et punkt P en hvilken som helst af koordinaterne (x, y), der hører til linjen, hvis koordinater ikke er kendt, og et andet punkt P₁ hvis koordinater er: (x₁,Y₁).

Hældningen er:

m = (y - y₁) / (x - x₁)

Vi kan rydde Y:

og - og₁ = m (x - x₁)

Antag nu, at punkt P₁ er krydset mellem linjen og den lodrette akse for koordinaterne (0, b). Udskiftning af dette i ovenstående ligning:

y - b = m (x - 0) → y = mx + b

Dette udtryk er kendt som linjens ligning i formen hældning - aflytning, da linjen bestemmes utvetydigt, når dens hældning og dens skæringspunkt med den lodrette akse er kendt.

Kun at vide hældningen er ikke nok til at karakterisere en linje på flyet, da uendelige linjer kan have samme hældning, hvilket betyder at de er parallelle, men passerer gennem andre punkter.

Løst øvelser

- Øvelse 1

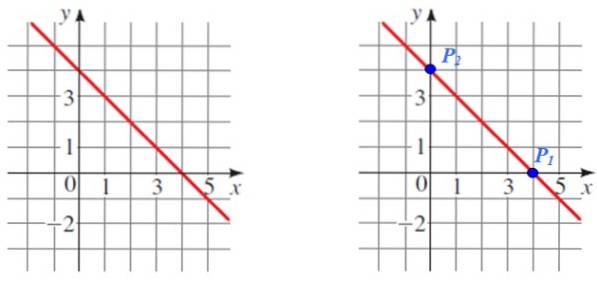
Find hældningen på linjen vist i følgende figur:

Opløsning

P₁ Og s_to er to letlæselige punkter, der vil blive brugt til beregningen, bemærk også, at de er de respektive skæringspunkter med koordinatakserne.

Koordinaterne for hvert punkt er:

P₁ (4.0) og P_to (0,4)

Ved at erstatte hældningen i ligningen:

m = (4 - 0) / (0 - 4) = 4 / (- 4) = -1

Hældningen er negativ, hvilket man kunne forvente efter at have set på grafen.

- Øvelse 2

Find ligningen for linjen, der passerer gennem punktet (1, -6) og er parallel med linjen y = 2x - 3.

Opløsning

Hældningen på den søgte linje skal være den samme som y = 2x - 3, da de er parallelle. For denne linje er hældningen m = 2, derfor har den vi leder efter formen:

og - og₁ = 2 (x - x₁)

Nu erstatter vi det punkt, gennem hvilket vores linje passerer: x₁ = 1 og y₁ = -6.

y - (-6) = 2 (x - 1)

Derfor er y = 2x - 2 - 6 → y = 2x - 8

Eksempler

To størrelser kan relateres på en sådan måde, at deres graf er en lige linje. I så fald siges det, at størrelserne har lineær afhængighed, og linjens hældning kan fortolkes som ændringshastigheden fra den ene variabel til den anden.

Eksempel 1

Antag at en pool er fyldt med vand ved en sats konstant i tiden. Jo mere tid der går, jo mere lagres vand naturligvis. Den hastighed, hvormed puljen er fyldt, er netop hældningen på linjen, der relaterer lydstyrken til tiden:

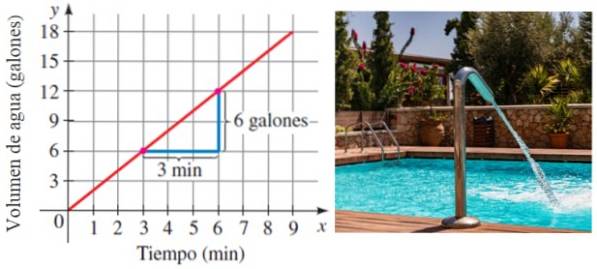
I dette eksempel fyldes puljen med en hastighed på 6/3 gallon pr. Minut eller 2 gallon / minut.

Eksempel 2

Når en mobil bevæger sig i en lige linje med konstant hastighed, er hældningen af ​​positionsgrafen som en funktion af tiden ingen ringere end den nævnte hastighed. Grafen viser en mobil med positiv hastighed, hvilket betyder at den bevæger sig væk fra oprindelsen.

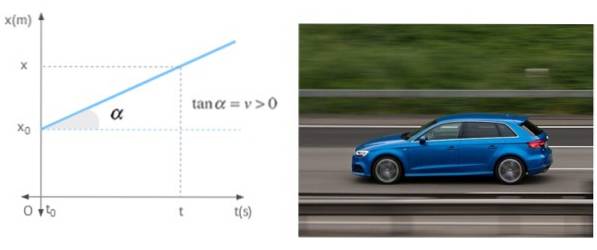
Referencer

1. Alvarez, J. En motorvejs skråning. Gendannet fra: geogebra.es.
2. Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
3. Hoffman, J. Selection of Mathematics Topics. Bind 4.
4. Jiménez, R. 2008. Algebra. Prentice hall.
5. Stewart, J. 2006. Precalculus: Matematik til beregning. 5. plads Udgave. Cengage læring.
6. Zill, D. 1984. Algebra og trigonometri. Mcgraw bakke.