
Skråt plan, hvad det er beregnet til, eksempler, øvelser
Det skråplan Det er en simpel maskine, der består af en flad overflade, der danner en vinkel i forhold til vandret. Formålet er at reducere den krævede indsats for at løfte en genstand til en bestemt højde.
En almindelig anvendelse er at løfte en tung last på en byggeplatform eller et køretøj. Erfaringsmæssigt ved vi, at på denne måde reduceres indsatsen mod at øge afstanden, der skal tilbagelægges lidt..
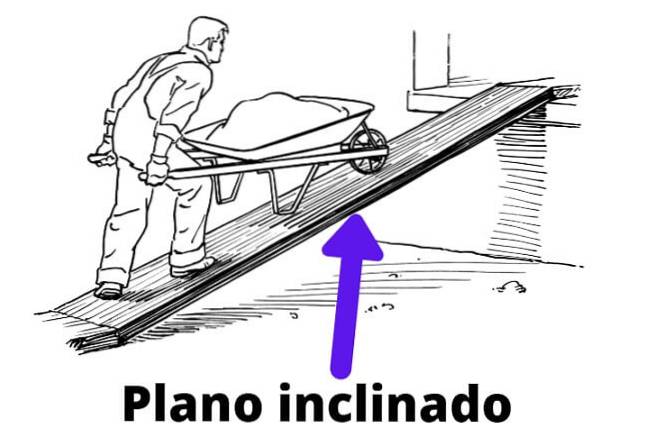
Så i stedet for at løfte genstanden lodret i en højde h, er den lavet til at køre en afstand d over overfladen af det skrå plan. Derefter bidrager overfladen til at afbalancere en del af genstandens vægt, specifikt den lodrette komponent af den samme.
Anvendt kraft F Det er ansvarligt for at flytte den vandrette komponent af vægten, hvis størrelse er mindre end selve vægten. Derfor er størrelsen af F er mindre end størrelsen af den krævede kraft til direkte at hæve kroppen.
Den krævede reduktion i krævet indsats kaldes mekanisk fordel, et princip opdaget af den store gamle fysiker Archimedes fra Syracuse (287-212 f.Kr.). Jo større den mekaniske fordel er, desto mindre indsats skal der gøres for at udføre opgaven.
Artikelindeks
- 1 Eksempler på skråplaner
- 1.1 Ramper
- 1.2 Kiler
- 1.3 Skruer
- 2 styrker, der virker på en genstand på et skråt plan
- 2.1 Normal og vægt
- 2.2 Normal, vægt og kinetisk friktion
- 3 Øvelse løst
- 3.1 Løsning
- 4 Referencer
Eksempler på skråplaner
Enkle maskiner som det skråplan har været kendt siden forhistorisk tid. Tidlige mennesker brugte skæreinstrumenter af sten til at fremstille pilespidser til at jage og skære træ for at lave redskaber..
Den mekaniske fordel M ved en simpel maskine defineres som kvotienten mellem størrelsen af udgangskraften og indgangskraftens. Det er derfor en dimensionsløs størrelse.
Normalt er outputkraftens størrelse større end inputkraften og M> 1. Men der er meget sarte opgaver, der fortjener en reduktion i outputkraften, som det er tilfældet med klemmerne, for hvilke M < 1.
Som eksempler på anvendelsen af det skrå plan har vi:
Ramper

Ramper er nyttige til at løfte tunge genstande til en bestemt højde, hvilket kræver anvendelse af en kraft af mindre størrelse end genstandens vægt..
Den mekaniske fordel M ved en glat rampe uden friktion beregnes ved at gøre kvotienten mellem dens længde, kaldet "d" og dens højde, betegnet som "h":
M = d / h
I praksis er der imidlertid friktion mellem overfladerne, derfor er den virkelige mekaniske fordel lidt mindre end M (se løst øvelse 2).
Kiler
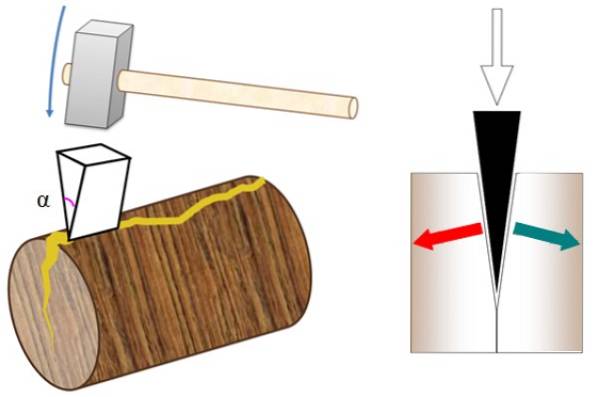
De består af et dobbelt skråt plan lavet af resistent materiale med to kontaktflader, der giver høje friktionskræfter på grund af skærekanten, der dannes på kanten..
Forkant er i stand til at overvinde materialets modstand og adskille det i stykker ved hjælp af en hammer for at anvende kraft. Brugen af kilen udvides ved at fastgøre et håndtag til den som en økse.
Knive, akser og mejsler er gode eksempler på brugen af kiler som skæreinstrumenter. Folks snitænder er også formet på denne måde for at skære mad i mindre, seje stykker.
Jo længere kilen er og jo mindre vinklen på skærekanten er, desto større er værktøjets mekaniske fordel, som gives ved:
M = 1 / tg α
Hvor α er vinklen ved forkant. Spidse former som kiler fungerer ikke kun for at overvinde træets modstand. Køretøjer såsom fly og både har også kileformer for at overvinde luftmodstand og få fart..
Skruer
Der er et skråt plan i en anden dagligdags enhed, der bruges til at fastgøre dele: skruen. Skruetråden er et skråt plan, der er viklet rundt om skruens cylindriske akse.
En indgangskraft påføres Fjeg til skruen, og når der drejes en omgang af størrelse 2πR, hvor R er radius, bevæger skruen sig en afstand p, kaldet Han gik forbi. Denne afstand er den, der adskiller to på hinanden følgende gevind på skruen.
Styrker, der handler på et objekt på et skråt plan
Normal og vægt
Figuren viser et frit legemsdiagram over et objekt på et plan skråtstillet i vinkel α. Under forudsætning af ingen friktion er de kræfter, der virker på objektet: de normale N, udøves vinkelret og W vægten, som er lodret.
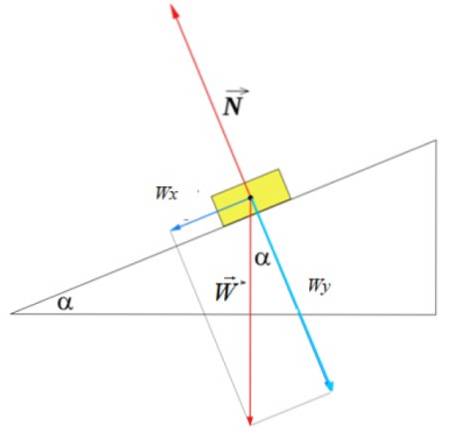
Komponenten af vægten i retning af det normale er WY, der kompenserer dette normale, da objektet ikke bevæger sig over planet, men parallelt med det. En styrke F anvendt på objektet skal i det mindste kompensere for W-komponentenx så objektet går op ad det skrå plan.
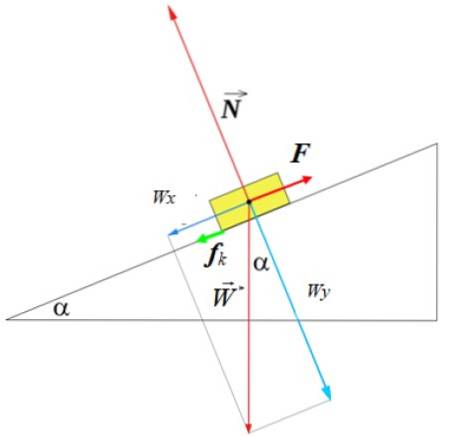
Normal, vægt og kinetisk friktion
Hvis friktion overvejes, skal det tages i betragtning, at den altid er imod bevægelse eller mulig bevægelse. Når objektet bevæger sig på overfladen af det skrå plan, virker den kinetiske friktion, hvis objektet går opad, den kinetiske friktion Fk den er rettet i den modsatte retning, og kraften F skal også have ansvaret for at besejre den.
Træning løst
Find den vinkel, som spidsen af en kil skal have, for at dens mekaniske fordel er 10.
Opløsning
I tidligere afsnit blev det fastslået, at den mekaniske fordel M ved kilen blev givet ved:
M = 1 / tg α
Hvis M skal være 10 værd:
1 / tg α = 10
tg α = 1/10 → α = 5,71º
Referencer
- E-skole i dag. Kilen. Gendannet fra: eschooltoday.com.
- Resnick, R. 1999. Fysik. Bind 1. 3. udgave på spansk. Compañía Editorial Continental S.A. af C.V.
- Rex, A. 2011. Grundlæggende fysik. Pearson.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1.
- Tippens, P. 2011. Fysik: begreber og applikationer. 7. udgave. Mcgraw bakke.
- Wikipedia. Skråplan. Gendannet fra: es.wikipedia.org.


Endnu ingen kommentarer