
Konveks polygondefinition, elementer, egenskaber, eksempler

EN konveks polygon det er en geometrisk figur indeholdt i et plan, der er karakteriseret, fordi det har alle sine diagonaler i dets indre og dets vinkler måler mindre end 180º. Blandt dens egenskaber er følgende:
1) Den består af n på hinanden følgende segmenter, hvor den sidste af segmenterne slutter sig til den første. 2) Ingen af segmenterne skærer hinanden på en sådan måde, at de afgrænser planet i et indre område og et ydre område. 3) Hver eneste vinkel i det indre område er strengt mindre end en plan vinkel.

En enkel måde at bestemme, om en polygon er konveks eller ej, er at overveje linjen, der passerer gennem en af dens sider, som bestemmer to halvplaner. Hvis i hver linje, der passerer gennem den ene side, de andre sider af polygonen er i samme halvplan, så er det en konveks polygon.
Artikelindeks
- 1 Elementer af en polygon
- 1.1 Konvekse og ikke-konvekse polygoner
- 2 Egenskaber for den konvekse polygon
- 2.1 Diagonaler og vinkler i konvekse polygoner
- 3 eksempler
- 3.1 Eksempel 1
- 3.2 Eksempel 2
Elementer af en polygon
Hver polygon består af følgende elementer:
- Sider
- Hjørner
Siderne er hver af de på hinanden følgende segmenter, der udgør polygonen. I en polygon kan ingen af de segmenter, der udgør den, have en åben ende, i så fald ville der være en polygonal linje, men ikke en polygon.
Højdepunkter er knudepunkterne for to på hinanden følgende segmenter. I en polygon er antallet af hjørner altid lig med antallet af sider.
Hvis to sider eller segmenter af en polygon krydser hinanden, har du en krydset polygon. Krydsningen betragtes ikke som et toppunkt. En krydspolygon er en ikke-konveks polygon. Stjernepolygoner er krydspolygoner og er derfor ikke konvekse.
Når en polygon har alle dens sider af samme længde, har vi en regelmæssig polygon. Alle regelmæssige polygoner er konvekse.
Konvekse og ikke-konvekse polygoner
Figur 1 viser flere polygoner, nogle af dem er konvekse og andre ikke. Lad os analysere dem:
Nummer 1 er en tre-sidet polygon (trekant), og alle indvendige vinkler er mindre end 180º, derfor er det en konveks polygon. Alle trekanter er konvekse polygoner.
Nummeret 2 er en firesidet polygon (firkant), hvor ingen af siderne krydser hinanden, og hver indvendige vinkel er mindre end 180 °. Det er derefter en konveks polygon med fire sider (konveks firkant).
På den anden side er tallet 3 en polygon med fire sider, men en af dens indvendige vinkler er større end 180 °, så det ikke opfylder konveksitetsbetingelsen. Det vil sige, det er en ikke-konveks firesidet polygon kaldet en konkav firkant..
Nummeret 4 er en polygon med fire segmenter (sider), hvoraf to skærer hinanden. De fire indvendige vinkler er mindre end 180 º, men da to sider krydser hinanden, er det en ikke-konveks krydset polygon (krydset firkant).
En anden sag er tallet 5. Dette er en femsidet polygon, men da en af dens indvendige vinkler er større end 180º, har vi en konkav polygon.
Endelig har tallet 6, som også har fem sider, alle sine indvendige vinkler mindre end 180 °, så det er en konveks polygon med fem sider (konveks femkant).
Egenskaber for den konvekse polygon
1- En ikke-krydset polygon eller simpel polygon deler planet, der indeholder det, i to regioner. Den indre region og den ydre region, hvor polygonen er grænsen mellem de to regioner.
Men hvis polygonen derudover er konveks, har vi et indre område, der simpelthen er tilsluttet, hvilket betyder, at hvis man tager to punkter fra det indre område, kan det altid være forbundet med et segment, der helt tilhører det indre område..
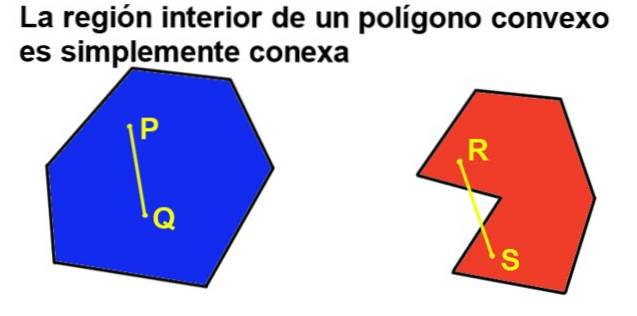
2- Enhver indvendig vinkel på en konveks polygon er mindre end en plan vinkel (180º).
3- Alle indvendige punkter i en konveks polygon hører altid til en af semiplanerne defineret af linjen, der passerer gennem to på hinanden følgende hjørner.
4- I en konveks polygon er alle diagonaler fuldstændigt indeholdt i det indre polygonale område.
5- De indvendige punkter i en konveks polygon hører udelukkende til den konvekse vinkelsektor defineret af hver indvendige vinkel.
6- Hver polygon, hvor alle dens hjørner er på en omkreds, er en konveks polygon, der kaldes en cyklisk polygon.
7- Hver cyklisk polygon er konveks, men ikke hver konveks polygon er cyklisk.
8- Enhver ikke-krydset polygon (enkel polygon), der har alle sider af samme længde, er konveks og er kendt som en regelmæssig polygon.
Diagonaler og vinkler i konvekse polygoner
9- Det samlede antal N diagonaler af en konveks polygon med n sider er givet ved følgende formel:
N = ½ n (n - 3)
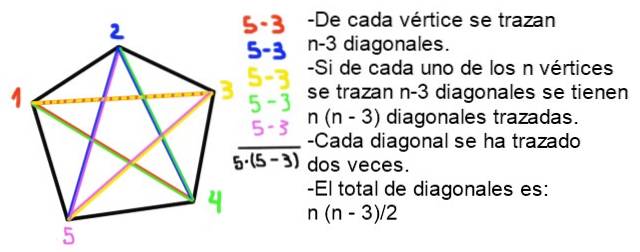
Bevis: I en konveks polygon med n sider af hvert toppunkt tegnes n - 3 diagonaler, da selve toppunktet og de to tilstødende er udelukket. Da der er n hjørner, tegnes n (n - 2) diagonaler i alt, men hver diagonal blev tegnet to gange, så antallet af diagonaler (uden gentagelse) er n (n-2) / 2.
10- Summen S af de indvendige vinkler af en konveks polygon med n sider er givet ved følgende forhold:
S = (n - 2) 180º
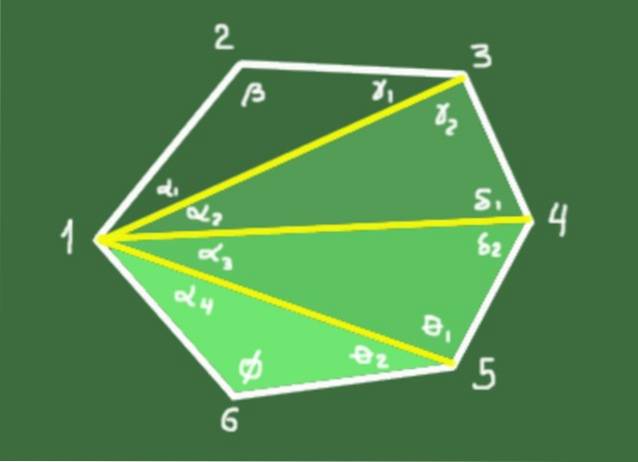
Bevis: Fra et toppunkt trækkes n-3 diagonaler, der definerer n-2 trekanter. Summen af de indre vinkler i hver trekant er 180º. Den samlede sum af vinklerne for n-2-trekanterne er (n-2) * 180º, hvilket falder sammen med summen af polygonens indre vinkler.
Eksempler
Eksempel 1
Cyklisk sekskant er en polygon med seks sider og seks hjørner, men alle hjørnerne har samme omkreds. Hver cyklisk polygon er konveks.
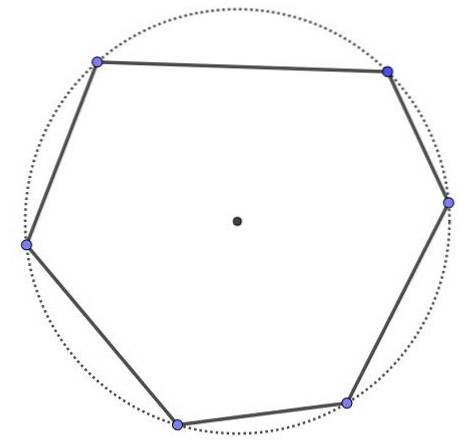
Eksempel 2
Bestem værdien af de indvendige vinkler for en regelmæssig enegon.
Løsning: Enegonen er en 9-sidet polygon, men hvis den også er regelmæssig, er alle dens sider og vinkler ens.
Summen af alle indvendige vinkler af en 9-sidet polygon er:
S = (9 - 2) 180º = 7 * 180º = 1260º
Men der er 9 interne vinkler med lige mål α, så følgende ligestilling skal være opfyldt:
S = 9 α = 1260º
Heraf følger, at målingen α for hver indre vinkel i den regulære enegon er:
α = 1260º / 9 = 140º



Endnu ingen kommentarer