
Regelmæssige polygonegenskaber, elementer, vinkler, eksempler
Det regelmæssige polygoner er dem, der har alle deres sider og deres indre vinkler ens. I den følgende figur er der et sæt forskellige polygoner, som er plane figurer begrænset af en lukket kurve, og kun de, der er fremhævet, opfylder betingelserne for at være regelmæssige.
For eksempel er den ligesidede trekant en regelmæssig polygon, da dens tre sider måler det samme såvel som dets indre vinkler, som hver er 60 ° værd..
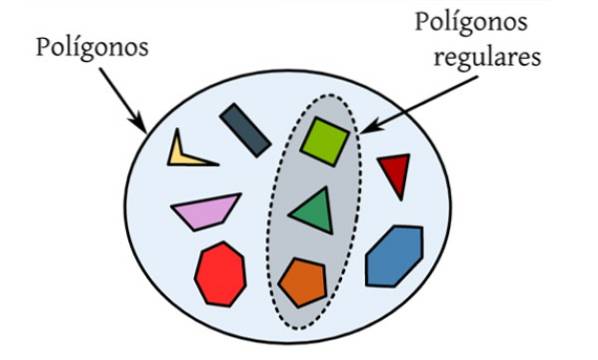
Firkanten er en firkant med fire sider af lige mål og hvis indre vinkler er 90º. Det efterfølges af den almindelige femkant med fem sider af samme størrelse og fem indre vinkler på hver 108 °..
Når en polygon er regelmæssig, tilføjes dette ord til dets specielle navn, så vi har den almindelige sekskant, den regelmæssige heptagon og så videre.
Artikelindeks
- 1 Egenskaber ved regelmæssige polygoner
- 2 Elementer af en regelmæssig polygon
- 2.1 Hvirvel
- 2.2 Side
- 2.3 Diagonal
- 2.4 Center
- 2.5 Radio
- 2.6 Apotem
- 2.7 Central vinkel
- 2.8 Sagita
- 3 Omkreds og areal
- 3.1 Omkreds
- 3.2 Område
- 4 vinkler
- 4.1 Central vinkel
- 4.2 Intern vinkel eller intern vinkel
- 4.3 Udvendige vinkler
- 5 eksempler på regelmæssige polygoner
- 5.1 - Regelmæssige polygoner i dagligdagen og naturen
- 5.2 - Regelmæssige sekskanter i naturen
- 6 Øvelse løst
- 6.1 Løsning
- 7 Referencer
Egenskaber ved regelmæssige polygoner
De vigtigste egenskaber ved regelmæssige polygoner kan opsummeres som følger:
-Siderne måler det samme, derfor er de også ligesidet.
-De er ækvivalent, da alle dens indre vinkler har samme mål.
-De kan altid være indskrevet i en omkreds, hvilket betyder at de passer perfekt inden for en, som kaldes omskrevet omkreds.
-For en regelmæssig polygon med n sider er målingen af en indvendig vinkel α:
a = [180 (n-2)] / n
-Du kan tegne n (n-3) / 2 diagonaler fra hjørnerne på en polygon, uanset om det er regelmæssigt eller ikke.
-Summen af udvendige vinkler er lig med 360º.

Elementer af en regelmæssig polygon
Dernæst præsenterer vi hovedelementerne i en regelmæssig polygon, visualiseret i nedenstående figur.

Hvirvel
Fælles punkt, som to på hinanden følgende sider har, betegnet som V i figuren.
Side
Det er segmentet, der forbinder to på hinanden følgende hjørner af polygonen og betegnes som ℓ eller L.
Diagonal
Segment, der forbinder to ikke-fortløbende hjørner af polygonen, i figuren er det betegnet som d.
Centrum
Det er det fælles centrum for den indskrevne cirkel og den omskrevne cirkel, betegnet med bogstavet O. Det kan også ses som det eneste punkt, der er lige langt fra både hjørnerne og midtpunkterne på hver side..
Radio
Det er radioen r af den omskrevne cirkel og falder sammen med afstanden mellem O og et toppunkt.
Apothem
Det kaldes apotem til radius af omkredsen indskrevet i polygonen, repræsenteret i figuren med et bogstav til. Apotemet er vinkelret på den ene side og forbinder det med centrum O (rødt segment i figur 3).
At kende radius r og længden af siden, beregnes apotemet af:
Da apotemet faktisk er et af benene i en højre trekant (se figur 3), det andet ben er værdien af ℓ / 2 (halvdelen af en side) og hypotenusen radius r af polygonen.
Når Pythagoras sætning anvendes på nævnte trekant, opnås denne ligning, som ikke kun er gyldig for sekskanten, men for enhver regelmæssig polygon.
Central vinkel
Det er den vinkel, hvis toppunkt falder sammen med centrum O, og hvis sider er segmenterne, der forbinder centrum med to på hinanden følgende hjørner. Dens mål i seksagesimale grader er 360º / n, hvor n er antallet af sider af polygonen.
Sagita
Det er forskellen mellem polygonens og apothemets radius (se figur 3). Betegner sagitta som S:
S = r - a
Omkreds og område
Omkreds
Det beregnes let ved at tilføje længderne på siderne. Da enhver side har samme længde L, og der er n sider, udtrykkes omkredsen P som:
P = n.L
Areal
I en regelmæssig polygon er området A givet af produktet mellem den halve omkreds (halvdelen af omkredsen) og længden af apotemet til.
A = P.a / 2
Da omkredsen afhænger af antallet af sider n, viser det sig at:
A = (nL) .a / 2
To regelmæssige polygoner kan have samme omkreds, selvom de ikke har det samme antal sider, da det derefter vil afhænge af længden af siderne.
I hans bog V Kollektion, matematikeren Pappus fra Alexandria (290-350), den sidste af de store antikke græske matematikere, viste at blandt alle de regelmæssige polygoner med samme omkreds er den med det største område den med det største antal sider.
Vinkler
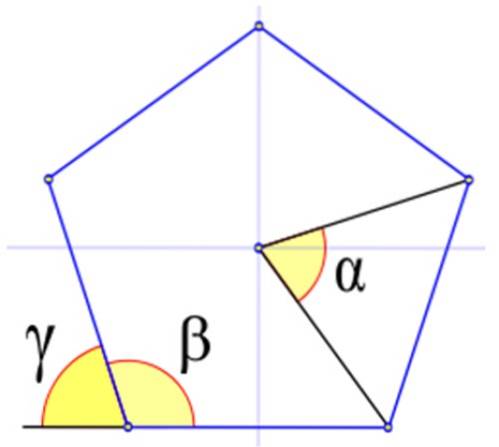
Figur 4 viser de relevante vinkler i en regelmæssig polygon betegnet med de græske bogstaver α, β og γ.
Central vinkel
Tidligere nævnte vi den centrale vinkel mellem elementerne i den almindelige polygon, det er den vinkel, hvis toppunkt er i midten af polygonen, og siderne er de segmenter, der forbinder centrum med to på hinanden følgende hjørner.
For at beregne mål for den centrale vinkel α divideres 360º med n, antallet af sider. Eller 2π radianer mellem n:
α = 360º / n
Ækvivalent i radianer til:
α = 2π / n
Intern vinkel eller intern vinkel
I figur 4 er den indvendige vinkel β den, hvis toppunkt falder sammen med en af figuren, og dens sider også er sider af figuren. Det beregnes i kønssimale grader af:
β = [180 (n-2)] / n
Eller i radianer ved hjælp af:
β = [π (n-2)] / n
Eksterne vinkler
De er betegnet med det græske bogstav γ. Figuren viser, at γ + β = 180º. Derfor:
γ = 180º - β
Summen af alle de eksterne vinkler til en almindelig polygon er 360º.

Eksempler på regelmæssige polygoner
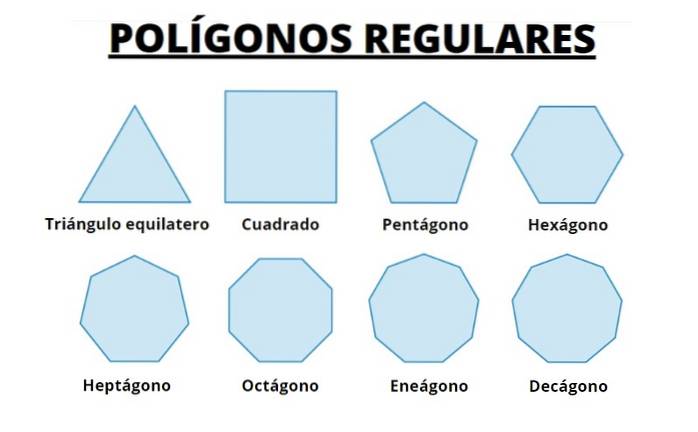
Dernæst har vi de første 8 regelmæssige polygoner. Vi bemærker, at når antallet af sider stiger, ligner polygonen i stigende grad den omkreds, som de er indskrevet i.
Vi kan forestille os, at ved at gøre længden af siderne mindre og mindre og øge antallet af disse får vi omkredsen.
- Regelmæssige polygoner i dagligdagen og naturen
Regelmæssige polygoner findes overalt i hverdagen og endda i naturen. Lad os se på nogle eksempler:
Trafiksignaler
Regelmæssige polygoner som ligesidede trekanter, firkanter og romber findes i overflod i de skiltninger, vi ser på motorveje og veje. I figur 6 ser vi et stopskilt med en ottekantet form.

Møbel
Utallige møbler har pladsen, for eksempel som deres karakteristiske geometriske figur, ligesom mange borde, stole og bænke er firkantede. En parallelepiped er generelt en kasse med sider i form af et rektangel (som ikke er en almindelig polygon), men de kan også gøres firkantede..
Arkitektur og konstruktion
Fliserne på gulve og vægge, både i hjem og på gaderne, er ofte formet som almindelige polygoner..
Tessellations er overflader dækket udelukkende med fliser, der har forskellige geometriske former. Med trekanten, firkanten og sekskanten kan du foretage regelmæssige tessellationer, dem der kun bruger en enkelt type figur til at dække perfekt uden at efterlade tomme rum (se figur 6).
Ligeledes bruger bygninger regelmæssige polygoner i elementer som vinduer og dekoration..

- Regelmæssige sekskanter i naturen
Overraskende nok er den regelmæssige sekskant en polygon, der ofte vises i naturen..
De kamme, der er lavet af bier til opbevaring af honning, er meget tæt på en almindelig sekskant. Som Pappus fra Alexandria observerede, optimerer bierne pladsen til at opbevare så meget honning som muligt..
Og der er også regelmæssige sekskanter i skildpaddernes skal og snefnugene, som også antager forskellige meget smukke geometriske former..
Træning løst
En regelmæssig sekskant er indskrevet i en halvcirkel med en radius på 6 cm, som vist på figuren. Hvad er værdien af det skraverede område?
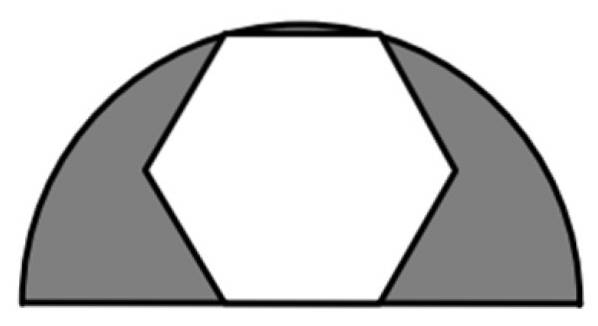
Opløsning
Det skraverede område er forskellen mellem halvcirkelens område med radius R = 6 cm og arealet af hele sekskanten, en regelmæssig 6-sidet polygon. Så vi har brug for formler til området for hver af disse figurer.
Halvcirkelområde
TIL1 = π Rto / 2 = π (6 cm)to / 2 = 18π cmto
Regelmæssigt sekskantet område
Formlen til beregning af arealet af en almindelig polygon er:
A = P.a / 2
Hvor P er omkredsen og til er apotemet. Da omkredsen er summen af siderne, har vi brug for værdien af disse. For den almindelige sekskant:
P = 6ℓ
Derfor:
A = 6ℓa / 2
For at finde værdien af siden ℓ er det nødvendigt at konstruere hjælpetal, som vi vil forklare nedenfor:
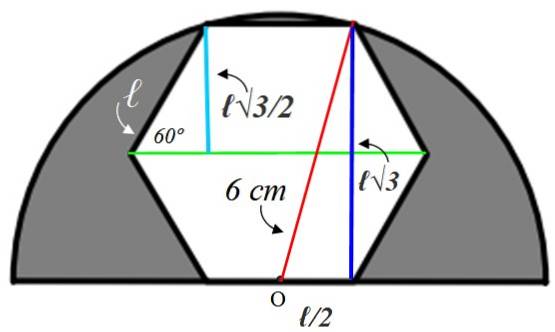
Lad os starte med den lille højre trekant til venstre, hvis hypotenus er ℓ. En indvendig vinkel på sekskanten er lig med:
α = [180 (n-2)] / n = α = [180 (6-2)] / 6 = 120º
Den radius, som vi har tegnet i grøn, halverer denne vinkel, så den lille trekants spidse vinkel er 60º. Med de givne oplysninger løses denne trekant og finder den lyseblå side, der måler det samme som apotemet:
Modsat ben = a = ℓ x sin 60º = ℓ√3 / 2 cm
Denne værdi det er det dobbelte af det mørkeblå ben af den store trekant til højre, men fra denne trekant ved vi, at hypotenusen måler 6 cm, fordi det er halvcirkelens radius. Det resterende ben (nederst) er lig med ℓ / 2, da punkt O er midt på siden.
Da indvendige vinkler af denne trekant ikke er kendt, kan vi angive Pythagoras sætning for det:
36 = 3 ℓto + ℓto / 4
(13/4) ℓto = 36 → ℓ = √ (4 x36) / 13 cm = 12 / √13 cm
Med denne værdi beregnes apotemet:
a = ℓ√3 / 2 cm = (12 / √13) x (√3 / 2) cm = 6√3 / √13 cm
Lad os ringeto til området med den almindelige sekskant:

= 28,8 cmto
Skraveret figurområde
TIL1 - TILto = 18π cmto - 28,8 cmto = 27,7 cmto
Referencer
- Baldor, A. 1973. Geometri og trigonometri. Centralamerikansk kulturforlag.
- Nyd matematik. Tessellations. Gendannet fra: gustolasmatematicas.com.
- E. A. 2003. Elementer af geometri: med øvelser og kompasgeometri. University of Medellin.
- Sekskanter i naturen. Gendannet fra: malvargamath.wordpress.com.
- Jiménez, R. 2010. Matematik II. Geometri og trigonometri. Anden version. Prentice hall.
- Regelmæssige polygoner. Gendannet fra: mate.ingenieria.usac.edu.gt.
- Wikipedia. Apothem. Gendannet fra: es.wikipedia.org.



Endnu ingen kommentarer