
Gage pres forklaring, formler, ligninger, eksempler
Det overtryk Pm er det, der måles i forhold til et referencetryk, som i de fleste tilfælde vælges som det atmosfæriske tryk Ppengeautomat ved havoverfladen. Det er så en relativ tryk, et andet udtryk, hvor det også er kendt.
Den anden måde, hvorpå tryk normalt måles, er ved at sammenligne det med absolut vakuum, hvis tryk altid er nul. I et sådant tilfælde taler vi om absolut pres, som vi vil betegne som Ptil.
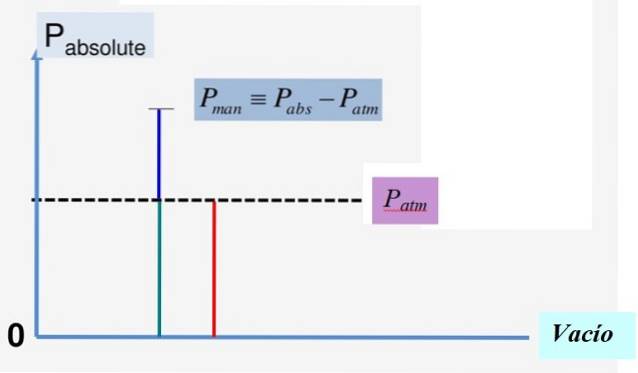
Det matematiske forhold mellem disse tre størrelser er:
Ptil = Ppengeautomat + Pm
Derfor:
Pm = Ptil - Ppengeautomat
Figur 1 illustrerer bekvemt dette forhold. Da vakuumtrykket er 0, er det absolutte tryk altid positivt, og det samme sker med atmosfæretrykket Ppengeautomat.
Målertryk bruges ofte til at betegne tryk over atmosfærisk tryk, såsom det der findes i dæk eller det i bunden af havet eller en swimmingpool, som udøves af vandsøjlens vægt. I disse tilfælde Pm > 0, da Ptil > Spengeautomat.
Der er imidlertid absolut pres under Ppengeautomat. I disse tilfælde Pm < 0 y recibe el nombre de Tryk fra tom og ikke forveksles med pres af vakuum, der allerede er beskrevet, hvilket er fraværet af partikler, der er i stand til at udøve tryk.
Artikelindeks
- 1 Formler og ligninger
- 1.1 Variation af tryk med dybde
- 2 Eksempler
- 2.1 Pascals princip
- 2.2 Stevins hydrostatiske paradoks
- 3 Øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 4 Referencer
Formler og ligninger
Trykket i en væske - væske eller gas - er en af de mest betydningsfulde variabler i dens undersøgelse. I en stationær væske er trykket det samme på alle punkter i den samme dybde uanset orientering, mens væskens bevægelse i rørene skyldes trykændringer..
Gennemsnitstryk defineres som kvotienten mellem kraften vinkelret på en overflade F⊥ og arealet af overfladen A, der udtrykkes matematisk som følger:
P = F⊥ /TIL
Tryk er en skalar størrelse, hvis dimensioner er kraft pr. Arealeenhed. Måleenhederne i det internationale system for enheder (SI) er newton / mto, kaldet Pascal og forkortet Pa til ære for Blaise Pascal (1623-1662).
Multipler som kilo (103) Y mega (106) anvendes ofte, da atmosfærisk tryk sædvanligvis ligger i området 90.000 - 102.000 Pa, hvilket er lig med: 90 - 102 kPa. Pres i størrelsesordenen megapascal er ikke ualmindelige, så det er vigtigt at gøre sig bekendt med præfikser.
I angelsaksiske enheder måles tryk i pund / fodto, dog gøres det normalt i pund / tommeto eller psi (pund-kraft pr. kvadrat tomme).
Variation af tryk med dybde
Jo mere vi fordyber os i vandet i en pool eller i havet, jo mere tryk oplever vi. Tværtimod, når højden øges, falder atmosfærisk tryk.
Det gennemsnitlige atmosfæriske tryk ved havoverfladen er fastsat til 101,300 Pa eller 101,3 kPa, mens det i Mariana-grøften i det vestlige Stillehav - den dybeste kendte dybde - er cirka 1000 gange større, og på toppen af Everest er det kun 34 kPa.
Det er klart, at tryk og dybde (eller højde) er relateret. For at finde ud af i tilfælde af en væske i hvile (statisk ligevægt) betragtes en skiveformet del af væske, der er begrænset i en beholder, (se figur 2). Skiven har tværsnitsareal TIL, vægt dW og højde D y.
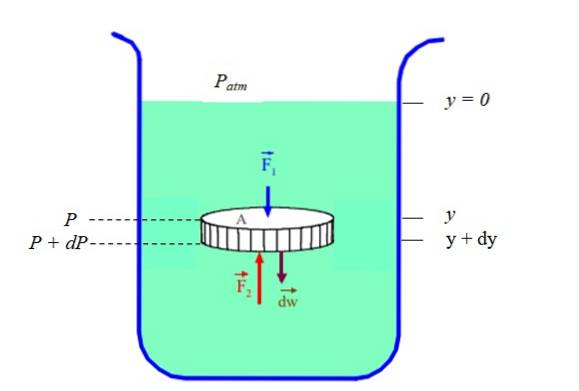
Vi ringer P til det pres, der findes i dybden "Y"Y P + dP til det tryk, der findes i dybden (y + dy). Da væskens densitet ρ er forholdet mellem dens masse dm og dens volumen dV, du skal:
ρ = dm / dV ⇒ dm = ρ.dV
Derfor vægten dW af elementet er:
dW = g. dm = ρ.g.dV
Og nu gælder Newtons anden lov:
Σ FY = Fto - F1 - dW = 0
(P + dP) .A - P.A - ρ.g.dV = 0
(P + dP) .A - P.A - ρ.g. A. dy = 0
dP = ρ.g.dy
Løsning af differentialligningen
Integrering af begge sider og i betragtning af, at densiteten ρ, såvel som tyngdekraften g er konstante, findes det søgte udtryk:
Pto - P1 = ΔP = ρ.g. (ogto - Y1)
ΔP = ρ.g. ΔY
Hvis du i det forrige udtryk vælger P1 som atmosfærisk tryk og Y1 som overfladen af væsken, så Yto det er placeret på en dybde h Y ΔP = Pto - Ppengeautomat er målertrykket som en funktion af dybde:
Pm = ρ.g.h
Hvis du har brug for den absolutte trykværdi, skal du blot tilføje det atmosfæriske tryk til det forrige resultat.
Eksempler
For at måle målerens tryk kaldes en enhed trykmåler, som generelt tilbyder trykforskelle. I slutningen vil arbejdsprincippet for et U-rør manometer blive beskrevet, men lad os nu se på nogle vigtige eksempler og konsekvenser af den tidligere udledte ligning.
Pascals princip
Ligningen ΔP = ρ.g. (ogto - Y1) kan skrives som P = Po + ρ.g.h, hvor P er trykket i dybden h, mens Peller er trykket ved væskens overflade, normalt Ppengeautomat.
Naturligvis hver gang det stiger Po, øges P i samme mængde, så længe det er en væske, hvis densitet er konstant. Det var præcis, hvad man skulle, når man overvejede ρ konstant og placer den uden for integralen, der blev løst i det foregående afsnit.
Pascals princip siger, at enhver stigning i trykket af en begrænset væske i ligevægt overføres uden nogen variation til alle punkter i væsken. Gennem denne egenskab er det muligt at multiplicere kraften F1 anvendt på det lille stempel til venstre og opnå Fto til højre.
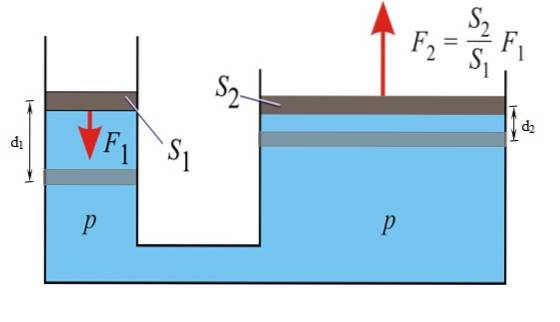
Bilbremser fungerer på dette princip: en relativt lille kraft påføres pedalen, som bliver en større kraft på bremsecylinderen ved hvert hjul takket være den væske, der bruges i systemet..
Stevins hydrostatiske paradoks
Det hydrostatiske paradoks angiver, at kraften på grund af trykket fra en væske i bunden af en beholder kan være lig med, større eller mindre end selve væskens vægt. Men når du lægger beholderen oven på skalaen, registrerer den normalt væskens vægt (plus beholderen selvfølgelig). Hvordan man forklarer dette paradoks?
Vi starter med det faktum, at trykket i bunden af beholderen udelukkende afhænger af dybden og er uafhængig af formen, som det blev udledt i det forrige afsnit.
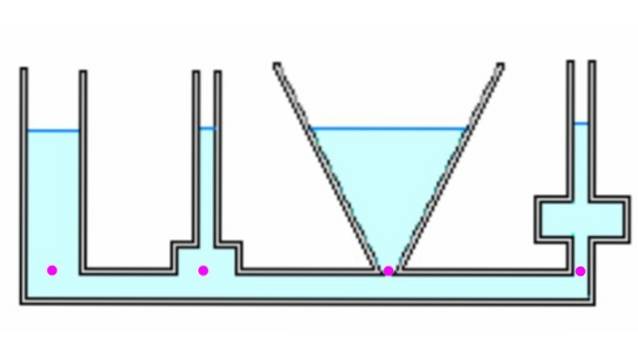
Lad os se på et par forskellige containere. Når de kommunikeres, når de fyldes med væske, når de alle samme højde h. Højdepunkterne er ved samme tryk, da de er i samme dybde. Kraften på grund af tryk ved hvert punkt kan dog afvige fra vægten, (se eksempel 1 nedenfor).
Uddannelse
Øvelse 1
Sammenlign den kraft, der udøves af trykket på bunden af hver af beholderne med væskens vægt, og forklar hvorfor forskellene, hvis nogen.
Beholder 1
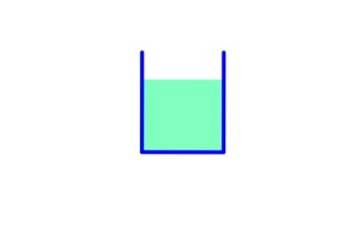
I denne container er basisarealet A, derfor:
Væskevægt: mg = ρ.V.g = ρ . A .h. g
Tryk på bunden: ρ. g. h
Kraft på grund af tryk: F = P.A = ρ. g. h. TIL
Vægt og kraft på grund af tryk er ens.
Beholder 2
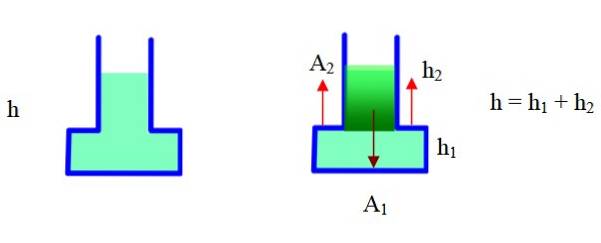
Containeren har en smal del og en bred del. I diagrammet til højre er det opdelt i to dele, og geometri vil blive brugt til at finde det samlede volumen. Område Ato det er ekstern til containeren, hto er højden af den smalle del, h1 er højden på den brede del (bund).
Den fulde lydstyrke er lydstyrken på basen + lydstyrken på den smalle del. Med disse data har vi:
Væskevægt: m. g = ρ . g. V = ρ . g. [TIL1 .h1+ (TIL1 -TILto) .hto] =
= ρ . g (A1.hatohto) = ρ . g. TIL1.h - ρ . g. TIL.. hto (Der er gjort brug af h = h1 +hto)
Tryk på bunden: P = ρ. g. h
Kraft på bunden på grund af tryk: F = P. A1 = ρ. g. h. TIL1
Sammenligning af væskens vægt med kraften på grund af tryk viser, at denne er større end vægten.
Hvad der sker er, at væsken også udøver kraft på den del af trinnet i beholderen (se pilene i rødt i figuren), der er inkluderet i ovenstående beregning. Denne opadgående kraft modvirker dem, der udøves nedad, og vægten registreret af skalaen er resultatet af disse. Ifølge dette er vægtenes størrelse:
W = Kraft på bunden - Kraft på den trinvise del = ρ . g. TIL1.h - ρ . g. TIL.. hto
Øvelse 2
Et åbent rørmanometer er vist i figuren. Det består af et U-formet rør, hvor den ene ende er ved atmosfærisk tryk, og den anden er forbundet til S, det system, hvis tryk skal måles..
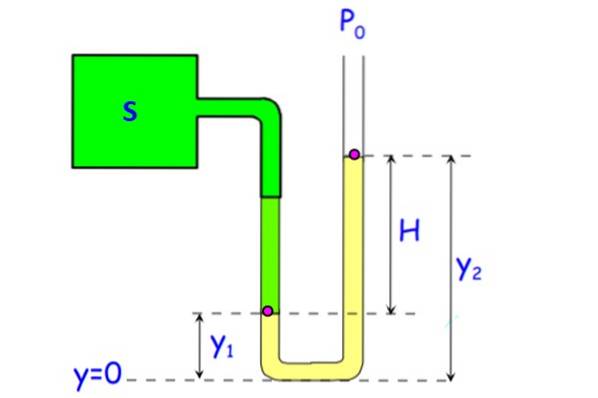
Væsken i røret (vist med gult på figuren) kan være vand, skønt kviksølv fortrinsvis anvendes til at reducere størrelsen på enheden. (En forskel på 1 atmosfære eller 101,3 kPa kræver en 10,3 meter vandsøjle, intet bærbart).
Det beder om at finde målerens tryk Pm i system S, som en funktion af væskesøjlens højde H.
Opløsning
Trykket i bunden for begge grene af røret er det samme, da de er i samme dybde. Lad PTIL trykket ved punkt A, placeret ved y1 Og sB dem i punkt B, der er i højden ogto. Da punkt B er ved grænsefladen mellem væske og luft, er trykket der Peller. I denne gren af manometeret er trykket i bunden:
Po + ρ.g.yto
For sin del er trykket i bunden for grenen til venstre:
P + ρ.g.y1
Hvor P er systemets absolutte tryk, og ρ er væskens tæthed. Udligning af begge tryk:
Po + ρ.g.yto = P + ρ.g.y1
Rydder ud P:
P = Po + ρ.g.yto - ρ.g.y1 = Po + ρ.g (ogto - Y1) = Po + ρ.g. H
Derfor måler tryk Pm er givet af P - Peller = ρ.g. H og for at få sin værdi skal du bare måle den højde, som den manometriske væske stiger til, og gang den med værdien af g og væskens tæthed.
Referencer
- Cimbala, C. 2006. Fluid Mechanics, Fundamentals and Applications. Mc. Graw Hill. 66-74.
- Figueroa, D. 2005. Serie: Physics for Sciences and Engineering. Volumen 4. Væsker og termodynamik. Redigeret af Douglas Figueroa (USB). 3-25.
- Mott, R. 2006. Fluid Mechanics. 4. plads Udgave. Pearson Uddannelse. 53-70.
- Shaugnessy, E. 2005. Introduktion til væskemekanik. Oxford University Press. 51 - 60.
- Stylianos, V. 2016. En enkel forklaring på det klassiske hydrostatiske paradoks. Gendannet fra: haimgaifman.files.wordpress.com


Endnu ingen kommentarer