
Første ligevægtstilstandsforklaring, eksempler, øvelser
Det første ligevægtstilstand kræver, at vektorsummen af alle kræfter, der virker på en krop, er nul, så den er i ro (statisk ligevægt) eller med ensartet retlinet bevægelse (dynamisk ligevægt).
Denne sum af kræfter er ingen ringere end nettokraften, der virker på kroppen, udtrykt matematisk på denne måde:
Fnet = 0
∑ F = 0

I rummet giver den første ligevægtsbetingelse tre ligninger, en for hver dimension:
∑ Fx = 0; ∑ FY = 0 og ∑ Fz = 0
Når disse ligninger er opfyldt, oversættes objektet ikke, eller hvis det gør det, vil det være med konstant hastighed.
Når vi ser os omkring, indser vi, at vi hele tiden søger at tilfredsstille den første betingelse for balance, så ting ikke falder.
Derfor søger den at kompensere jordens tyngdekraft ved hjælp af understøtninger, reb eller understøtninger fra nogle, så tingene på denne måde forbliver på plads og ikke ender på jorden..
Andre gange er det nødvendige, at forhindre eksterne elektromagnetiske felter i at forstyrre driften af elektriske kredsløb og kommunikationsenheder. I dette tilfælde er det de elektriske ladninger, der skal være i ligevægt..
Artikelindeks
- 1 Eksempler
- 1.1 Bygninger
- 1.2 Trafiklys og hængende skilte
- 1.3 Ledere i elektrostatisk ligevægt
- 1.4 Loftlamper
- 1.5 Bøger og genstande på bordene
- 1.6 Måling af en væskes viskositet
- 2 trin til at anvende den første ligevægtstilstand
- 3 Løst øvelser
- 3.1 - Øvelse løst 1
- 3.2 - Øvelse løst 2
- 4 Emner af interesse
- 5 Referencer
Eksempler
Et stort antal hverdagsgenstande tilfredsstiller den første betingelse af ligevægt, det er et spørgsmål om nøje at observere:
Bygninger
Bygherrer søger stabilitet i konstruktioner, så brugerne forbliver sikre. Formålet med statik er at undersøge forholdene for statisk ligevægt i bygninger, broer, veje og alle slags strukturer..
Trafiklys og hængende skilte
Disse signalanordninger skal forblive faste for at udføre deres funktioner, derfor holdes de af kabler, stænger og stænger på en sådan måde, at den første ligevægtsbetingelse er opfyldt..

Ledere i elektrostens ligevægtpenthouse
Når ledende materialer såsom kobber og andre metaller erhverver en elektrisk ladning, etableres elektrostatisk ligevægt hurtigt, hvilket efterlader den overskydende ladning på den ledende overflade. Inde i det elektriske felt er nul.
Denne effekt bruges ofte til at isolere elektrisk og elektronisk udstyr fra eksterne felter ved hjælp af det såkaldte Faraday-bur. Buret er lavet af ledende materiale og omgiver det udstyr, der skal beskyttes.
Under storme tjener biler som Faraday-bure ved at beskytte passagerer mod elektriske stød..
Loftlamper
I belysningssystemer, såsom vedhængslamper, bruges den første ligevægtsbetingelse til at fastgøre dem til loftet, gulvet eller væggen.

Bøger og genstande på borde
Genstande placeret på borde og hylder opfylder den første ligevægtstilstand. Den normale kraft, som støtten udøver på genstandene, er ansvarlig for at kompensere for vægten.
Måling af viskositeten af en væske
For at bestemme en væskes viskositet falder et kugleformet objekt med kendt diameter i dets indre, og dets hastighed vil blive langsommere på grund af modstand. Kuglens hastighed er konstant og er således i dynamisk ligevægt.
Jo højere væskens viskositet er, desto lavere hastighed hvormed kuglen bevæger sig indeni.
Trin til at anvende den første ligevægtstilstand
-Lav et fritlegemsdiagram, der viser alle de kræfter, der virker på kroppen (udelad dem, som kroppen udøver på andre).
-Vælg et kartesisk koordinatsystem, og sørg for, at kræfterne så vidt muligt er placeret på en hvilken som helst af akserne. Den positive retning tages normalt i bevægelsesretningen eller en mulig bevægelse.
-Bestem de kartesiske komponenter i hver styrke.
-Anvendelse af Newtons anden lov for hver komponent, som oprettet i begyndelsen, forbliver således et ligningssystem.
-Løs ligningssystemet, der blev rejst i det foregående trin.
Løst øvelser
- Løst øvelse 1
Blokken af figuren, af masse m, den bevæger sig ned ad bakke på det skrånende plan i vinklen θ med konstant hastighed. Beregn værdien af kinetisk friktionskoefficient μk, hvis massen af blokken er m = 5 kg og θ = 37º.

Opløsning
Det første trin er at tegne fritlegemsdiagrammet og vælge et kartesisk koordinatsystem til at udtrykke hver kraft vektor. De kræfter, der virker på blokken, er:
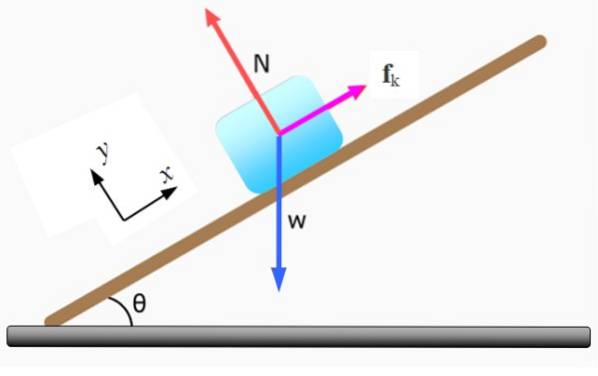
-Det normale N udøves af det skrånende plan, er vinkelret på overfladen af dette.
-Vægten W er lodret lodret nedad.
-Kinetisk friktion Fk der er imod bevægelse. Hvis den ikke eksisterede, bevæger kroppen sig ned ad bakke med en acceleration svarende til g.senθ.
Ligesom vægt W er skråtstillet i forhold til de valgte koordinatakser, skal den nedbrydes i dens kartesiske komponenter:
Wx = mg sin 37º = 5 kg x 9,8 m / sto x sin 37º = 29. 5 N
WY = mg.cos 37º = 5 kg x 9,8 m / sto x cos 37º = 39,1 N
Newtons anden lov anvendes nu, idet hver sum indstilles til 0, da blokken mangler acceleration, når den bevæger sig med konstant hastighed:
∑ FY = N - WY = 0
∑ Fx = Wx - Fk = 0
Størrelsen af den kinetiske friktion er proportional med størrelsen af det normale, idet kinetisk friktionskoefficient er μk proportionalitetskonstanten.
Fk = μk N
På samme tid:
N = WY = 39,1 N
Plus:
Fk = Wx
Derfor:
- 5 N = μk x 39,1 N
μk = 29. 5 / 39,1 = 0,75
- Træning løst 2
Beregn størrelsen af de belastninger, der understøtter trafiklyset med en masse på 33 kg, vist i figuren:
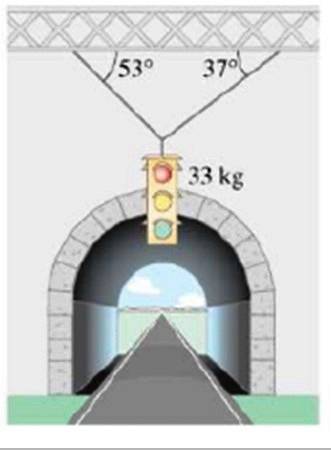
Opløsning
Free-body-diagrammet er lavet til både trafiklyset og den knude, der holder kablerne:
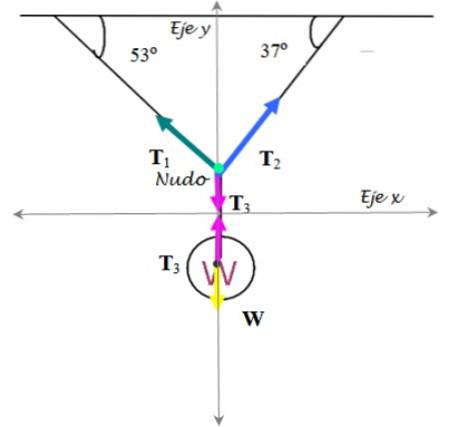
Trafiklys
På det handler: spændingen T3 op og W vægt ned. Derfor:
∑ FY = W - T3 = 0
Derfor:
T3 = 33 kg x 9,8 m / sto = 323,4 N
Knude
Spændingerne nedbrydes i deres kartesiske komponenter:
∑ FY = T1 sin 53º + Tto sen 37º - T3 = 0
∑ Fx = Tto cos 37º - T1 cos 53º = 0
Og følgende system med lineære ligninger opnås med to ukendte T1 og Tto :
- 0,6 T1 + 0,8 Tto = 0
0,8 T1 + 0,6 Tto = 323,4
Løsningen af dette ligningssystem er: T1 = 258,7 N og Tto = 194,0 N
Temaer af interesse
Ligevægtsbetingelser.
Anden ligevægtstilstand.
Referencer
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 4. Partikelsystemer. Redigeret af Douglas Figueroa (USB).
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1.
- Wikipedia. Statisk (mekanisk). Gendannet fra: es.wikipedia.org.


Endnu ingen kommentarer