
Frekvenssandsynlighedskoncept, hvordan det beregnes og eksempler
Det frekvens sandsynlighed er en underdefinition inden for undersøgelsen af sandsynligheden og dens fænomener. Hans studiemetode med hensyn til begivenheder og attributter er baseret på store mængder iterationer og observerer således trenden for hver enkelt på lang sigt eller endda ved uendelige gentagelser..
For eksempel indeholder en konvolut med gummier 5 viskelæder af hver farve: blå, rød, grøn og gul. Vi ønsker at bestemme sandsynligheden for, at hver farve skal komme ud efter et tilfældigt valg.

Det er kedeligt at forestille sig at tage en gummi ud, registrere den, returnere den, tage en gummi ud og gentage den samme ting flere hundrede eller flere tusinde gange. Du vil måske endda observere adfærden efter flere millioner iterationer.
Men tværtimod er det interessant at opdage, at den forventede sandsynlighed på 25% efter nogle få gentagelser ikke er fuldt ud opfyldt, i det mindste ikke for alle farver efter 100 gentagelser er sket..
Under tilgangen af frekvenssandsynligheden vil tildelingen af værdierne kun ske gennem studiet af mange iterationer. På denne måde skal processen udføres og registreres fortrinsvis på en computeriseret eller efterlignet måde.
Flere strømme afviser frekvenssandsynligheden og argumenterer for manglende empiri og pålidelighed i tilfældighedskriterierne.
Artikelindeks
- 1 Hvordan beregnes frekvenssandsynligheden?
- 1.1 Lov om stort antal
- 2 Andre tilgange til sandsynlighed
- 2.1 Logisk teori
- 2.2 Subjektiv teori
- 3 Historie
- 3.1 Massefænomener og gentagne begivenheder
- 3.2 Attributter
- 4 Eksempel
- 4.1 Referencer
Hvordan beregnes frekvenssandsynligheden?
Ved at programmere eksperimentet i en hvilken som helst grænseflade, der er i stand til at tilbyde en rent tilfældig iteration, kan man begynde at studere frekvenssandsynligheden for fænomenet ved hjælp af en værditabel.
Det forrige eksempel kan ses fra frekvensmetoden:
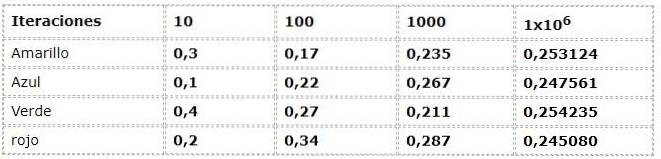
De numeriske data svarer til udtrykket:
N (a) = antal forekomster / antal iterationer
Hvor N (a) repræsenterer den relative hyppighed af begivenheden "a"
"A" hører til sættet med mulige resultater eller prøveplads Ω
Ω: rød, grøn, blå, gul
En betydelig spredning er værdsat i de første iterationer, når man observerer frekvenser med op til 30% forskelle mellem dem, hvilket er meget høje data for et eksperiment, der teoretisk har begivenheder med samme mulighed (Equiprobable).
Men efterhånden som gentagelserne vokser, synes værdierne at tilpasse sig mere og mere til dem, der præsenteres af den teoretiske og logiske strøm.
Lov om de store tal
Som en uventet aftale mellem den teoretiske og frekvensmetoden opstår loven om stort antal. Hvor det er fastslået, at værdierne for frekvenseksperimentet nærmer sig de teoretiske værdier efter et betydeligt antal iterationer.
I eksemplet kan du se, hvordan værdierne nærmer sig 0.250, når iterationerne vokser. Dette fænomen er elementært i konklusionerne fra mange sandsynlige værker.

Andre tilgange til sandsynlighed
Der er 2 andre teorier eller tilgange til begrebet sandsynlighed ud over frekvens sandsynlighed.
Logisk teori
Hans tilgang er orienteret mod den deduktive logik af fænomener. I det foregående eksempel er sandsynligheden for at opnå hver farve 25% på en lukket måde. Det vil sige, at deres definitioner og aksiomer ikke overvejer forsinkelser uden for deres rækkevidde af sandsynlige data..
Subjektiv teori
Det er baseret på den viden og tidligere tro, som hver enkelt har om fænomener og attributter. Udsagn som “Det regner altid i påsken " De skyldes et mønster af lignende begivenheder, der tidligere har fundet sted.
Historie
Begyndelsen af dens implementering går tilbage til det 19. århundrede, da Venn citerede det i flere af sine værker i Cambridge England. Men det var først langt ind i det tyvende århundrede, at 2 statistiske matematikere udviklede og formede frekvens sandsynlighed.
En af dem var Hans Reichenbach, der udvikler sit arbejde i publikationer som "The Theory of Probability" udgivet i 1949.
Den anden var Richard Von Mises, som videreudviklede sit arbejde gennem flere publikationer og foreslog at overveje sandsynligheden som en matematisk videnskab. Dette koncept var nyt for matematik og ville indlede en æra med vækst i studiet af matematik. frekvens sandsynlighed.
Faktisk markerer denne begivenhed den eneste forskel med bidrag fra Venn, Cournot og Helm generationen. Hvor sandsynligheden bliver homolog med videnskaber som geometri og mekanik.
< La teoría de las probabilidades trata con massive fænomener og gentagne begivenheder. Problemer, hvor enten den samme begivenhed gentages igen og igen, eller et stort antal ensartede elementer er involveret på samme tid> Richard Von Mises
Massive fænomener og gentagne begivenheder
Tre typer kan klassificeres:
- Fysisk: de adlyder naturmønstre ud over en tilstand af tilfældighed. For eksempel opførslen af molekylerne i et element i en prøve.
- Chance - Din primære overvejelse er tilfældighed, såsom at rulle en matrix gentagne gange.
- Biologiske statistikker: valg af forsøgspersoner i henhold til deres egenskaber og egenskaber.
I teorien spiller den person, der måler, en rolle i de sandsynlige data, fordi det er deres viden og erfaringer, der artikulerer denne værdi eller forudsigelse..
I frekvens sandsynlighed begivenhederne betragtes som samlinger, der skal behandles, hvor individet ikke spiller nogen rolle i estimeringen.
Egenskaber
En attribut forekommer i hvert element, som vil variere alt efter dets natur. For eksempel, i den type fysiske fænomen, vil vandmolekylerne have forskellige hastigheder..
I terningkastet kender vi prøveområdet Ω, der repræsenterer eksperimentets attributter.
Ω: 1, 2, 3, 4, 5, 6
Der er andre attributter som at være lige ΩP eller være ulige Ωjeg
Ωs : 2, 4, 6
Ωjeg : 1, 3, 5
Hvilket kan defineres som ikke-elementære attributter.
Eksempel
- Vi ønsker at beregne hyppigheden af hver mulig sammenfatning ved kaste af to terninger.
Til dette programmeres et eksperiment, hvor to kilder til tilfældige værdier mellem [1, 6] tilføjes i hver iteration.
Data registreres i en tabel, og tendenser i stort antal undersøges.
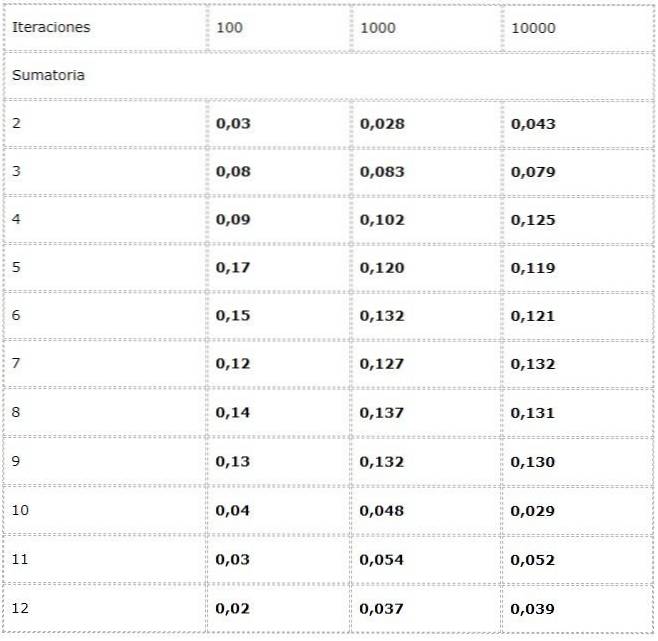
Det observeres, at resultaterne kan variere betydeligt mellem gentagelserne. Imidlertid kan loven om stort antal ses i den tilsyneladende konvergens, der er præsenteret i de sidste to kolonner.
Referencer
- Statistik og evaluering af bevis for retsmedicinske forskere. Anden version. Colin G.G. Aitken. Matematisk Skole. University of Edinburgh, Storbritannien
- Matematik til datalogi. Eric Lehman. Google Inc..
F Thomson Leighton Institut for Matematik og Computer Science and AI Laboratory, Massachusetts Institute of Technology; Akamai Technologies - Den aritmetiske lærer, bind 29. National Council of Teachers of Mathematics, 1981. University of Michigan.
- Læring og undervisning talteori: Forskning i kognition og instruktion / redigeret af Stephen R. Campbell og Rina Zazkis. Ablex udgivelse 88 Post Road West, Westport CT 06881
- Bernoulli, J. (1987). Ars Conjectandi- 4ème partie. Rouen: IREM.



Endnu ingen kommentarer