Det teoretisk sandsynlighed (eller Laplace), at en begivenhed E forekommer, der hører til et prøveområde S, hvor alle begivenheder har samme sandsynlighed for forekomst, er defineret i matematisk notation som: P (E) = n (E) / N (S)
Hvor P (E) er sandsynligheden, givet som kvotienten mellem det samlede antal mulige resultater af begivenheden E, som vi kalder n (E) divideret med det samlede antal N (S) af mulige resultater i prøveområdet S.
Den teoretiske sandsynlighed er et reelt tal mellem 0 og 1, men det udtrykkes ofte som en procentdel, i hvilket tilfælde sandsynligheden vil være en værdi mellem 0% og 100%.
Beregning af sandsynligheden for en begivenhed er meget vigtig inden for mange områder, såsom handel, forsikringsselskaber, spil og mange flere..
Artikelindeks
Et illustrativt tilfælde er tilfældet med lodtrækninger eller lotterier. Antag, at der udstedes 1.000 billetter til lodtrækning af en smartphone. Da lodtrækningen udføres tilfældigt, har en af billetterne lige chance for at blive en vinder.
For at finde sandsynligheden for, at en person, der køber en billet med nummeret 81, er en vinder, følgende beregning af teoretisk sandsynlighed:
P (1) = 1/1000 = 0,001 = 0,1%
Det forrige resultat fortolkes som følger: hvis lodtrækningen blev gentaget uendeligt mange gange, ville hver 1.000 gange billet 81 i gennemsnit blive valgt en gang.
Hvis nogen af en eller anden grund får alle billetterne, er det sikkert, at de vinder prisen. Sandsynligheden for at vinde prisen, hvis du har alle billetterne, beregnes som følger:
P (1.000) = 1.000 / 1.000 = 1 = 100%.
Det vil sige, at sandsynligheden 1 eller 100% betyder, at det er helt sikkert, at dette resultat vil forekomme..
Hvis nogen ejer 500 billetter, er chancerne for at vinde eller tabe den samme. Den teoretiske sandsynlighed for at vinde prisen i dette tilfælde beregnes som følger:
P (500) = 500 / 1.000 = ½ = 0.5 = 50%.
Den, der ikke køber nogen billet, har ingen chance for at vinde, og hans teoretiske sandsynlighed bestemmes som følger:
P (0) = 0 / 1.000 = 0 = 0%
Du har en mønt med dyrt på den ene side og skjold eller stempel på den anden. Når mønten kastes, hvad er den teoretiske sandsynlighed for, at den kommer op hoveder??
P (dyrt) = n (dyrt) / N ( ansigt + skjold ) = ½ = 0,5 = 50%
Resultatet fortolkes som følger: hvis der blev lavet et stort antal kast, ville en af dem i gennemsnit i hver 2 kast komme op hoveder.
Procentvis er fortolkningen af resultatet, at udførelse af et uendeligt stort antal kast, i gennemsnit ud af 100 af dem 50 ville resultere i hoveder.
I en kasse er der 3 blå kugler, 2 røde kugler og 1 grønne. Hvad er den teoretiske sandsynlighed for, at når du tager en marmor ud af kassen, vil den være rød?
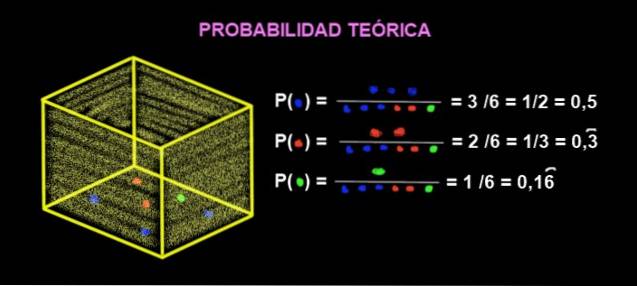
Sandsynligheden for, at den kommer rødt ud, er:
P (rød) = Antal gunstige sager / Antal mulige sager
Nemlig:
P (rød) = Antal røde kugler / Samlet antal kugler
Endelig er sandsynligheden for, at der tegnes en rød marmor:
P (rød) = 2/6 = ⅓ = 0,33333 = 33,33%
Mens sandsynligheden for, at når man tegner en grøn marmor, er:
P (grøn) = ⅙ = 0,1666 = 16,66%
Endelig er den teoretiske sandsynlighed for at opnå en blå marmor i en blind ekstraktion:
P (blå) = 3/6 = ½ = 0,5 = 50%
Det vil sige, for hvert 2. forsøg vil resultatet være blå i et af dem og en anden farve i et andet forsøg, under forudsætning af, at den ekstraherede marmor erstattes, og at antallet af forsøg er meget, meget stort..
Bestem sandsynligheden for, at der ved rulning af en matrix opnås en værdi på mindre end eller lig med 4.
For at beregne sandsynligheden for, at denne begivenhed finder sted, anvendes definitionen af teoretisk sandsynlighed:
P (≤4) = Antal gunstige sager / Antal mulige sager
P (≤5) = 5/6 = = 83,33%
Find sandsynligheden for, at 5 ved to på hinanden følgende kast af en normal seks-sidet matrice ruller 2 gange.
For at besvare denne øvelse er det praktisk at lave en tabel, der viser alle mulighederne. Det første ciffer angiver resultatet af den første dør og det andet resultatet af den anden.
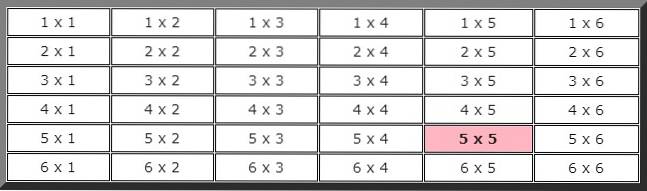
For at beregne den teoretiske sandsynlighed er vi nødt til at kende det samlede antal mulige tilfælde, i dette tilfælde, som det kan ses fra den foregående tabel, er der 36 muligheder.
Når man også observerer tabellen, kan det udledes, at antallet af sager, der er gunstige for den begivenhed, at der i de to på hinanden følgende lanceringer kun er 5 kun er fremhævet med farve, derfor er sandsynligheden for, at denne begivenhed opstår:
P (5 x 5) = 1/36.
Dette resultat kunne også være nået ved hjælp af en af egenskaberne for teoretisk sandsynlighed, som siger, at den kombinerede sandsynlighed for to uafhængige begivenheder er produktet af deres individuelle sandsynligheder..
I dette tilfælde er sandsynligheden for, at det første kast vil rulle 5, ⅙. Det andet kast er helt uafhængigt af det første, derfor er sandsynligheden for, at 5 rulles i det andet også ⅙. Så den kombinerede sandsynlighed er:
P (5 × 5) = P (5) P (5) = (1/6) (1/6) = 1/36.
Find sandsynligheden for, at et nummer mindre end 2 rulles ved første kast og et nummer større end 2 rulles på det andet.
Igen skal der bygges en tabel over mulige begivenheder, hvor de, hvor det første kast var mindre end 2 og i det andet større end 2, er fremhævet..
I alt er der 4 muligheder ud af i alt 36. Det vil sige, at sandsynligheden for denne begivenhed er:
P (<2 ; >2) = 4/36 = 1/9 = 0.1111 = 11.11%
Brug af sandsynlighedssætningen, der siger:
Sandsynligheden for forekomst af to uafhængige begivenheder er lig med produktet af de enkelte sandsynligheder.
Det samme resultat opnås:
P (<2) P(>2) = (1/6) (4/6) = 4/36 = 0,1111 = 11,11%
Værdien opnået med denne procedure falder sammen med det foregående resultat gennem den teoretiske eller klassiske definition af sandsynlighed.
Hvad er sandsynligheden for, at når rullende to terninger er summen af værdierne 7.
For at finde løsningen i dette tilfælde er der udarbejdet en tabel over muligheder, hvor de tilfælde, der opfylder betingelsen om, at summen af værdierne er 7, er angivet i farve.
Ser man på tabellen, kan 6 mulige tilfælde tælles, så sandsynligheden er:
P (I + II: 7) = 6/36 = 1/6 = 0,1666 = 16,66%
Endnu ingen kommentarer