
Egenskaber, applikationer og øvelser på tværs af produkter
Det krydsprodukt eller vektorprodukt det er en måde at multiplicere to eller flere vektorer på. Der er tre måder at multiplicere vektorer på, men ingen af disse er multiplikation i ordets sædvanlige forstand. En af disse former er kendt som et vektorprodukt, hvilket giver os som et resultat en tredje vektor.
Korsproduktet, som også kaldes krydsproduktet eller det ydre produkt, har forskellige algebraiske og geometriske egenskaber. Disse egenskaber er meget nyttige, især i studiet af fysik..

Artikelindeks
- 1 Definition
- 2 egenskaber
- 2.1 Ejendom 1
- 2.2 Ejendom 2
- 2.3 Ejendom 3
- 2.4 Ejendom 4 (produkt med tre prikker)
- 2.5 Ejendom 5 (tredobbelt vektorprodukt)
- 2.6 Ejendom 6
- 2.7 Ejendom 7
- 2.8 Ejendom 8
- 3 applikationer
- 3.1 Beregning af volumenet af en parallelepiped
- 4 Løst øvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Referencer
Definition
En formel definition af vektorproduktet er følgende: hvis A = (a1, a2, a3) og B = (b1, b2, b3) er vektorer, så er vektorproduktet af A og B, som vi betegner som AxB, er:
AxB = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
På grund af AxB-notationen læses den som "A cross B".
Et eksempel på, hvordan man bruger det ydre produkt er, at hvis A = (1, 2, 3) og B = (3, -2, 4) er vektorer, så bruger definitionen af et vektorprodukt, vi har:
AxB = (1, 2, 3) x (3, -2, 4) = (2 * 4 - 3 * (- 2), 3 * 3 - 1 * 4, 1 * (- 2) - 2 * 3)
AxB = (8 + 6, 9 - 4, - 2 - 6) = (14, 5, - 8).
En anden måde at udtrykke vektorproduktet på er angivet ved hjælp af determinanter.
Beregningen af en anden ordensdeterminant gives ved:
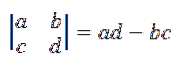
Derfor kan formlen for krydsproduktet, der er givet i definitionen, omskrives som følger:
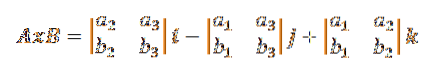
Dette forenkles normalt til en tredje ordens determinant som følger:
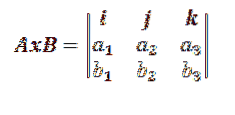
Hvor i, j, k repræsenterer vektorerne, der danner grundlaget for R3.
Ved at bruge denne måde at udtrykke tværproduktet på, har vi, at det foregående eksempel kan omskrives som:
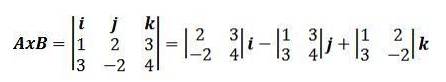
Ejendomme
Nogle egenskaber, som vektorproduktet besidder, er følgende:
Ejendom 1
Hvis A er en hvilken som helst vektor i R3, vi skal:
- AxA = 0
- Ax0 = 0
- 0xA = 0
Disse egenskaber er nemme at kontrollere ved hjælp af kun definitionen. Hvis A = (a1, a2, a3) har vi:
AxA = (a2a3 - a3a2, a3a1 - a1a3, a1a2 - a2a1) = (0, 0, 0) = 0.
Ax0 = (a2 * 0 - a3 * 0, a3 * 0 - a1 * 0, a1 * 0 - a2 * 0) = (0, 0, 0) = 0.
Hvis i, j, k repræsenterer enhedsgrundlaget for R3, vi kan skrive dem som følger:
i = (1, 0, 0)
j = (0, 1, 0)
k = (0, 0, 1)
Så vi har, at følgende egenskaber er sande:
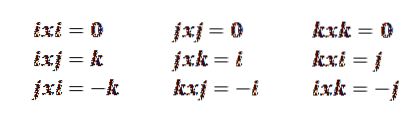
Som en mindesregel bruges følgende cirkel ofte til at huske disse egenskaber:
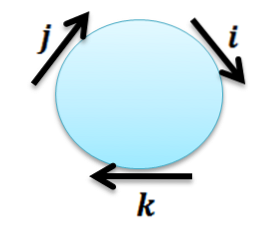
Der skal vi bemærke, at enhver vektor med sig selv giver vektor 0 som et resultat, og resten af produkterne kan opnås med følgende regel:
Tværproduktet af to på hinanden følgende vektorer i retning med uret giver den næste vektor; og når der betragtes mod uret, er resultatet følgende vektor med negativt tegn.
Takket være disse egenskaber kan vi se, at vektorproduktet ikke er kommutativt; for eksempel skal du bare bemærke, at i x j ≠ j x i. Den følgende egenskab fortæller os, hvordan AxB og BxA generelt er relateret.
Ejendom 2
Hvis A og B er vektorer af R3, vi skal:
AxB = - (BxA).
Demonstration
Hvis A = (a1, a2, a3) og B = (b1, b2, b3), har vi pr. Definition af eksternt produkt:
AxB = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
= (- 1) (a3b2 - a2b3, a1b3 - a3b1, a2b1 - a1b2)
= (- 1) (BxA).
Vi kan også se, at dette produkt ikke er associeret med følgende eksempel:
ix (ixj) = ixk = - j men (ixi) xj = 0xj = 0
Ud fra dette kan vi se, at:
ix (ixj) ≠ (ixi) xj
Ejendom 3
Hvis A, B, C er vektorer af R3 og r er et reelt tal, følgende er sandt:
- Axe (B + C) = AxB + AxC
- r (AxB) = (rA) xB = Ax (rB)
Takket være disse egenskaber kan vi beregne vektorproduktet ved hjælp af algebra, forudsat at ordren overholdes. For eksempel:
Hvis A = (1, 2, 3) og B = (3, -2, 4), kan vi omskrive dem baseret på den kanoniske basis af R3.
Således er A = i + 2j + 3k og B = 3i - 2j + 4k. Brug derefter de tidligere egenskaber:
AxB = (i + 2j + 3k) x (3i - 2j + 4k)
= 3 (ixi) - 2 (ixj) + 4 (ixk) + 6 (jxi) - 4 (jxj) + 8 (jxk) + 9 (kxi) - 6 (kxj) +12 (kxk)
= 3 (0) - 2 (k) + 4 (- j) + 6 (- k) - 4 (0) + 8 (i) + 9 (j) - 6 (- i) +12 (0)
= - 2k - 4j - 6k + 8i + 9j + 6i = 14i + 5j - 4k
= (14, 5, - 8).
Ejendom 4 (produkt med tredobbelt prik)
Som vi nævnte i starten, er der andre måder at multiplicere vektorer ud over vektorproduktet. En af disse måder er det skalære produkt eller det indre produkt, der betegnes som A ∙ B, og hvis definition er:
Hvis A = (a1, a2, a3) og B = (b1, b2, b3), så er A ∙ B = a1b1 + a2b2 + a3b3
Ejendommen, der vedrører begge produkter, er kendt som det tredobbelte skalarprodukt.
Hvis A, B og C er vektorer af R3, derefter A ∙ BxC = AxB ∙ C
Lad os som et eksempel se, at givet A = (1, 1, - 2), B = (- 3, 4, 2) og C = (- 5, 1, - 4), er denne egenskab opfyldt.
BxC = - 3k - 12j + 20k - 16i - 10j - 2i = - 18i - 22j + 17k
A ∙ BxC = (1, 1, - 2) ∙ (- 18, - 22, 17) = (1) (- 18) + (1) (- 22) + (- 2) (17) = - 74
På den anden side:
AxB = 4k - 2j + 3k + 2i + 6j + 8i = 10i + 4j + 7k
AxB ∙ C = (10, 4, 7) ∙ (- 5, 1, - 4) = (10) (- 5) + (4) (1) + (7) (- 4) = - 74
Et andet tredobbelt produkt er Axe (BxC), der er kendt som det tredobbelte vektorprodukt..
Ejendom 5 (tredobbelt vektorprodukt)
Hvis A, B og C er vektorer af R3, derefter:
Axe (BxC) = (A ∙ C) B - (A ∙ B) C
Lad os som et eksempel se, at givet A = (1, 1, - 2), B = (- 3, 4, 2) og C = (- 5, 1, - 4), er denne egenskab opfyldt.
Fra det foregående eksempel ved vi, at BxC = (- 18, - 22, 17). Lad os beregne Ax (BxC):
Axe (BxC) = - 22k - 17j + 18k + 17i + 36j - 44i = - 27i + 19j - 4k
På den anden side er vi nødt til at:
A ∙ C = (1, 1, - 2) ∙ (- 5, 1, - 4) = (1) (- 5) + (1) (1) + (- 2) (- 4) = - 5 + 1 + 8 = 4
A ∙ B = (1, 1, - 2) ∙ (- 3, 4, 2) = (1) (- 3) + (1) (4) + (- 2) (2) = - 3 + 4 - 4 = - 3
Således skal vi:
(A ∙ C) B - (A ∙ B) C = 4 (- 3, 4, 2) + 3 (- 5, 1, - 4) = (- 12, 16, 8) + (- 15, 3, - 12) = (- 27,19, -4)
Ejendom 6
Det er en af vektorernes geometriske egenskaber. Hvis A og B er to vektorer i R3 og ϴ er vinklen dannet mellem disse, så:
|| AxB || = || A |||| B || sin (ϴ), hvor || ∙ || angiver modulet eller størrelsen af en vektor.
Den geometriske fortolkning af denne egenskab er som følger:
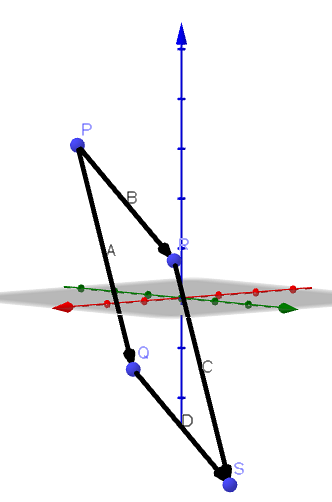
Lad A = PR og B = PQ. Derefter er vinklen dannet af vektorerne A og B vinklen P for trekanten RQP, som vist i den følgende figur.
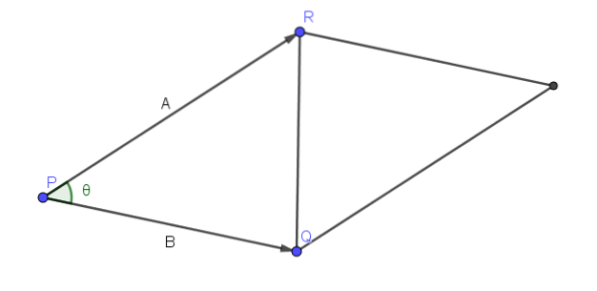
Derfor er arealet af parallelogrammet, der har PR og PQ som tilstødende sider, || A |||| B || sin (ϴ), da vi kan tage som basis || A || og dens højde er givet af || B || sin (ϴ).
Ved dette kan vi konkludere, at || AxB || er området for parallelogrammet.
Eksempel
Givet de følgende hjørner af en firkant P (1, -2,3), Q (4, 3, -1), R (2, 2,1) og S (5,7, -3), viser, at nævnte firkant er et parallelogram og find dets område.
Til dette bestemmer vi først vektorerne, der bestemmer retningen af firsidens sider. Dette er:
A = PQ = (1 - 4, 3 + 2, - 1 - 3) = (3, 5, - 4)
B = PR = (2 - 1, 2 + 2, 1 - 3) = (1, 4, - 2)
C = RS = (5 - 2, 7 - 2, - 3 - 1) = (3, 5, - 4)
D = QS = (5 - 4, 7 - 3, - 3 + 1) = (1, 4, - 2)
Som vi kan se, har A og C den samme direktørvektor, så vi har, at begge er parallelle; det samme sker med B og D. Derfor konkluderer vi, at PQRS er et parallelogram.
For at få arealet af dette parallelogram beregner vi BxA:
BxA = (i + 4j - 2k) x (3i + 5j - 4k)
= 5k + 4j - 12k - 16i - 6j + 10i
= - 6i - 2j - 7k.
Derfor vil det kvadratiske område være:
|| BxA ||to = (- 6)to + (- to)to + (- 7)to = 36 + 4 + 49 = 89.
Det kan konkluderes, at parallelogramområdet vil være kvadratroden på 89.
Ejendom 7
To vektorer A og B er parallelle i R3 hvis og kun hvis AxB = 0
Demonstration
Det er klart, at hvis A eller B er nulvektoren, bliver det opfyldt, at AxB = 0. Da nulvektoren er parallel med enhver anden vektor, er ejendommen gyldig.
Hvis ingen af de to vektorer er nulvektoren, har vi, at deres størrelser er forskellige fra nul; det vil sige begge || A || ≠ 0 som || B || ≠ 0, så vi har || AxB || = 0 hvis og kun hvis sin (ϴ) = 0, og dette sker hvis og kun hvis ϴ = π eller ϴ = 0.
Derfor kan vi konkludere AxB = 0 hvis og kun hvis ϴ = π eller ϴ = 0, hvilket kun sker, når begge vektorer er parallelle med hinanden.
Ejendom 8
Hvis A og B er to vektorer i R3, så er AxB vinkelret på både A og B.
Demonstration
For dette bevis skal vi huske, at to vektorer er vinkelrette, hvis A ∙ B er lig med nul. Desuden ved vi, at:
A ∙ AxB = AxA ∙ B, men AxA er lig med 0. Derfor har vi:
A ∙ AxB = 0 ∙ B = 0.
Ved dette kan vi konkludere, at A og AxB er vinkelrette på hinanden. På samme måde skal vi:
AxB ∙ B = A ∙ BxB.
Da BxB = 0, har vi:
AxB ∙ B = A ∙ 0 = 0.
Derfor er AxB og B vinkelret på hinanden, og med dette demonstreres egenskaben. Dette er meget nyttigt, da det giver os mulighed for at bestemme ligningen af et plan.
Eksempel 1
Få en ligning af planet, der passerer gennem punkterne P (1, 3, 2), Q (3, - 2, 2) og R (2, 1, 3).
Lad A = QR = (2 - 3.1 + 2, 3 - 2) og B = PR = (2 - 1.1 - 3, 3 - 2). Derefter A = - i + 3j + k og B = i - 2j + k. For at finde det plan, der er dannet af disse tre punkter, er det nok at finde en vektor, der er normal for planet, som er AxB.
AxB = (- i + 3j + k) x (i - 2j + k) = 5i + 2j - k.
Med denne vektor og tager punktet P (1, 3, 2) kan vi bestemme ligningen af planet som følger:
(5, 2, - 1) ∙ (x - 1, y - 3, z - 2) = 5 (x - 1) + 2 (y - 3) - (z - 2) = 0
Således har vi, at ligningen af planet er 5x + 2y - z - 9 = 0.
Eksempel 2
Find ligningen for det plan, der indeholder punktet P (4, 0, - 2), og som er vinkelret på hvert af planene x - y + z = 0 og 2x + y - 4z - 5 = 0 .
Når vi ved, at en normal vektor til en plan akse + med + cz + d = 0 er (a, b, c), har vi, at (1, -1,1) er en normal vektor af x - y + z = 0 y (2,1, - 4) er en normal vektor på 2x + y - 4z - 5 = 0.
Derfor skal en normal vektor til det søgte plan være vinkelret på (1, -1,1) og til (2, 1, - 4). Nævnte vektor er:
(1, -1,1) x (2,1, - 4) = 3i + 6j + 3k.
Derefter har vi, at det søgte plan er det, der indeholder punktet P (4,0, - 2) og har vektoren (3,6,3) som en normal vektor.
3 (x - 4) + 6 (y - 0) + 3 (z + 2) = 0
x + 2y + z - 2 = 0.
Ansøgninger
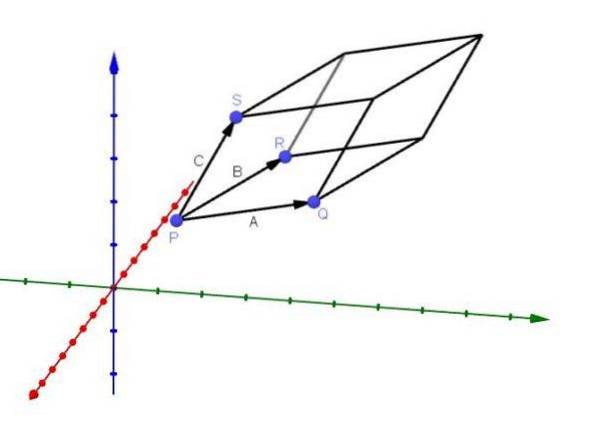
Beregning af volumen af en parallelepiped
En applikation, der har det tredobbelte skalære produkt, er at kunne beregne volumenet af en parallelepiped, hvis kanter er givet af vektorerne A, B og C, som vist i figuren:
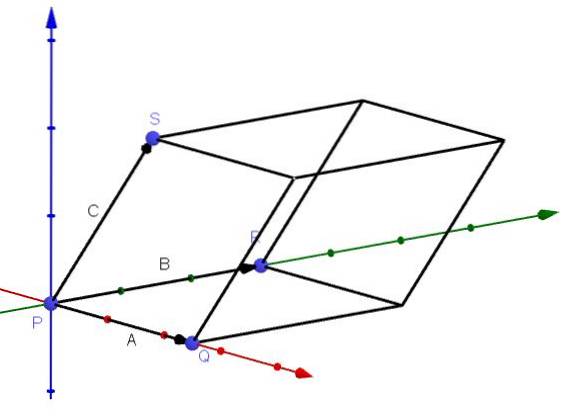
Vi kan udlede denne anvendelse på følgende måde: som vi sagde før, er vektoren AxB en vektor, der er normal i forhold til planet A og B. Vi har også, at vektoren - (AxB) er en anden vektor, der er normal i forhold til planet.
Vi vælger den normale vektor, der danner den mindste vinkel med vektor C; uden tab af generalitet, lad AxB være den vektor, hvis vinkel med C er den mindste.
Vi har, at både AxB og C har det samme udgangspunkt. Desuden ved vi, at arealet af parallelogrammet, der danner bunden af parallelepiped, er || AxB ||. Derfor, hvis højden på parallelepiped er givet af h, har vi, at dens volumen vil være:
V = || AxB || h.
Lad os på den anden side overveje det skalære produkt mellem AxB og C, som kan beskrives som følger:
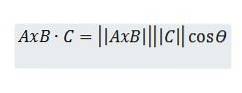
Imidlertid har vi ved trigonometriske egenskaber, at h = || C || cos (ϴ), så vi har:
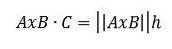
På denne måde har vi det:
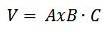
Generelt har vi, at volumenet af en parallelepiped er givet af den absolutte værdi af det tredobbelte skalære produkt AxB ∙ C.
Løst øvelser
Øvelse 1
Givet punkterne P = (5, 4, 5), Q = (4, 10, 6), R = (1, 8, 7) og S = (2, 6, 9), disse punkter danner en parallelepiped hvis kanter de er PQ, PR og PS. Bestem volumenet af parallelepiped.
Opløsning
Hvis vi tager:
- A = PQ = (-1, 6, 1)
- B = PR = (-4, 4, 2)
- C = PS = (-3, 2, 2)
Ved hjælp af egenskaben til det tredobbelte skalære produkt har vi:
AxB = (-1, 6, 1) x (-4, 4, 2) = (8, -2, 20).
AxB ∙ C = (8, -2, 20) ∙ (-3, 2, 2) = -24 -4 +80 = 52.
Derfor har vi, at volumenet af parallelepiped er 52.
Øvelse 2
Bestem volumenet af en parallelepiped, hvis kanter er givet af A = PQ, B = PR og C = PS, hvor punkterne P, Q, R og S er (1, 3, 4), (3, 5, 3), (2, 1, 6) og (2, 2, 5), henholdsvis.
Opløsning
Først har vi, at A = (2, 2, -1), B = (1, -2, 2), C = (1, -1, 1).
Vi beregner AxB = (2, 2, -1) x (1, -2, 2) = (2, -5, -6).
Derefter beregner vi AxB ∙ C:
AxB ∙ C = (2, -5, -6) ∙ (1, -1, 1) = 2 + 5 - 6 = 1.
Således konkluderer vi, at volumenet af den parallelepiped er 1 kubik enhed.
Referencer
- Leithold, L. (1992). Beregningen med analytisk geometri. HARLA, S.A.
- Resnick, R., Halliday, D., & Krane, K. (2001). Fysik bind 1. Mexico: Kontinentalt.
- Saenz, J. (s.f.). Vector Calculus 1ed. Hypotenus.
- Spiegel, M. R. (2011). Vektoranalyse 2ed. Mc Graw Hill.
- Zill, D. G., og Wright, W. (2011). Beregning af flere variabler 4ed. Mc Graw Hill.


Endnu ingen kommentarer