
Ikke-lineære programmeringsmetoder og øvelser
Det ikke-lineær programmering er processen med at optimere en funktion, der afhænger af flere uafhængige variabler, som igen er underlagt begrænsninger.
Hvis en eller flere af begrænsningerne, eller hvis funktionen til at maksimere eller minimere (kaldet Objektiv funktion), det udtrykkes ikke som en lineær kombination af variablerne, så vi har et ikke-lineært programmeringsproblem.
Og derfor kan procedurerne og metoderne til lineær programmering ikke bruges.
For eksempel kan den velkendte metode ikke bruges Simplex, hvilket kun gælder, når den objektive funktion og begrænsningerne alle er lineære kombinationer af problemvariablerne.
Artikelindeks
- 1 Metoder til lineær programmering
- 1.1 Eksempel på opløsning med grafisk metode
- 2 Øvelser
- 2.1 - Øvelse 1 (grafisk metode)
- 2.2 - Øvelse 2 (Analytisk metode: Lagrange-multiplikatorer)
- 2.3 - Øvelse 3 (Null gradient)
- 3 Referencer
Lineære programmeringsmetoder
For ikke-lineære programmeringsproblemer er de vigtigste metoder, der skal anvendes:
1.- Grafiske metoder.
2.- Lagrange-multiplikatorer for at udforske grænsen for løsningsområdet.
3.- Beregning af gradienten for at udforske ekstreme objektive funktioner.
4.- Metoden til faldende trin for at finde null-gradientpunkter.
5.- Modificeret metode til Lagrange-multiplikatorer (med Karush-Kuhn-Tucker-tilstand).
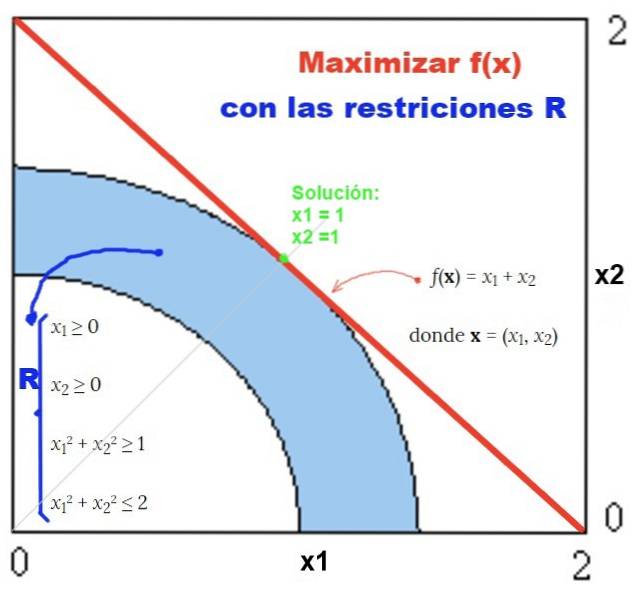
Eksempel på løsning med grafisk metode
Et eksempel på en løsning med den grafiske metode er den, der kan ses i figur 2:
Uddannelse
- Øvelse 1 (grafisk metode)
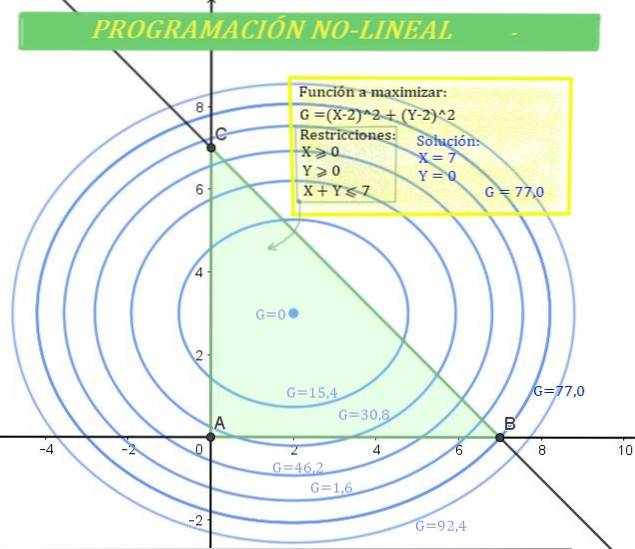
Overskuddet G for et bestemt selskab afhænger af det solgte beløb for produkt X og det solgte beløb for produkt Y, desuden bestemmes overskuddet af følgende formel:
G = 2 (X - 2)to + 3 (OG - 3)to
Det er kendt, at beløb X og Y har følgende begrænsninger:
X≥0; Y≥0 og X + Y ≤ 7
Bestem værdierne for X og Y, der giver den maksimale forstærkning.
Opløsning
I dette problem er den objektive funktion ikke-lineær, mens de uligheder, der definerer begrænsningerne, er. Det er et problem med ikke-lineær programmering.
Til løsning af dette problem vælges den grafiske metode.
Først vil løsningsområdet blive bestemt, hvilket er givet af begrænsningerne.
Som X≥0; Y≥0, løsningen skal findes i XY-planets første kvadrant, men da det også skal være sandt, at X + Y ≤ 7, er løsningen i det nederste halvplan af linjen X + Y = 7.
Løsningsområdet er skæringspunktet mellem den første kvadrant og det nederste halvplan af linjen, hvilket giver anledning til et trekantet område, hvor løsningen findes. Det er det samme som angivet i figur 1.
På den anden side kan forstærkningen G også være repræsenteret i det kartesiske plan, da dens ligning er en ellips med centrum (2,3).
Ellipsen er vist i figur 1 for forskellige værdier af G. Jo højere værdien af G, jo større er forstærkningen..
Der er løsninger, der hører til regionen, men som ikke giver den maksimale G-værdi, mens andre, såsom G = 92,4, er uden for den grønne zone, det vil sige løsningszonen.
Derefter svarer den maksimale værdi af G, således at X og Y hører til løsningsområdet, til:
G = 77 (maksimal forstærkning), som er givet for X = 7 og Y = 0.
Interessant nok opstår den maksimale fortjeneste, når salgsbeløbet for produkt Y er nul, mens mængden af produkt X når den højest mulige værdi..
- Øvelse 2 (analytisk metode: Lagrange-multiplikatorer)
Find den løsning (x, y), der gør funktionen f (x, y) = xto + 2 ogto være maksimum i regionen g (x, y) = xto + Yto - 1 = 0.
Opløsning
Det er helt klart et ikke-lineært programmeringsproblem, da både den objektive funktion f (x, y) og begrænsningen g (x, y) = 0 ikke er en lineær kombination af variablerne x og y.
Lagrange-multiplikatormetoden vil blive brugt, hvilket først kræver definition af Lagrange-funktionen L (x, y, λ):
L (x, y, λ) = f (x, y) - λ g (x, y) = xto + 2 ogto - λ (xto + Yto - 1)
Hvor λ er en parameter med navnet Lagrange multiplikator.
Følg disse trin for at bestemme de ekstreme værdier for den objektive funktion f i løsningsområdet givet ved begrænsningen g (x, y) = 0:
-Find delderivaterne af Lagrange-funktionen L med hensyn til x, y, λ.
-Sæt hvert derivat til nul.
Her er rækkefølgen af disse operationer:
- ∂L / ∂x = 2x - 2λx = 0
- ∂L / ∂y = 4y - 2λy = 0
- ∂L / ∂λ = - (xto + Yto - 1) = 0
Mulige systemløsninger
En mulig løsning af dette system er λ = 1, så den første ligning er opfyldt, i hvilket tilfælde y = 0, så den anden er opfyldt.
Denne løsning indebærer, at x = 1 eller x = -1 for at den tredje ligning skal opfyldes. På denne måde er der opnået to løsninger S1 og S2:
S1: (x = 1, y = 0)
S2: (x = -1, y = 0).
Det andet alternativ er, at λ = 2, så den anden ligning er opfyldt, uanset værdien y.
I dette tilfælde er den eneste måde, hvorpå den første ligning kan opfyldes, at x = 0. I betragtning af den tredje ligning er der kun to mulige løsninger, som vi vil kalde S3 og S4:
S3: (x = 0, y = 1)
S4: (x = 0, y = -1)
For at finde ud af, hvilken eller hvilke af disse løsninger, der maksimerer objektivfunktionen, fortsætter vi med at erstatte f (x, y):
S1: f (1, 0) = 1to + 2.0to = 1
S2: f (-1, 0) = (-1)to + 2.0to = 1
S3: f (0, 1) = 0to + 2.1to = 2
S4: f (0, -1) = 0to + enogtyve)to = 2
Vi konkluderer, at de løsninger, der maksimerer f, når x og y hører til omkredsen g (x, y) = 0 er S3 og S4.
Værdiparene (x = 0, y = 1) og (x = 0, y = -1) maksimerer f (x, y) i opløsningsområdet g (x, y) = 0.
- Øvelse 3 (Nul gradient)
Find løsninger (x, y) til den objektive funktion:
f (x, y) = xto + 2 ogto
Lad være maksimum i regionen g (x, y) = xto + Yto - 1 ≤ 0.
Opløsning
Denne øvelse svarer til øvelse 2, men løsningsområdet (eller begrænsningen) strækker sig til det indre område af omkredsen g (x, y) = 0, det vil sige til cirklen g (x, y) ≤ 0. Dette inkluderer til omkredsen og dens indre region.
Løsningen ved grænsen er allerede fastlagt i øvelse 2, men det indre område er stadig at undersøges.
For at gøre dette skal gradienten af funktionen f (x, y) beregnes og sættes lig med nul for at finde ekstreme værdier i løsningsområdet. Dette svarer til beregning af de partielle derivater af f med hensyn til henholdsvis x og y og indstilling lig med nul:
∂f / ∂x = 2 x = 0
∂f / ∂y = 4 y = 0
Dette ligningssystem har som den eneste løsning (x = 0, y = 0), der hører til cirklen g (x, y) ≤ 0.
Udskiftning af denne værdi i funktionen f resulterer i:
f (0, 0) = 0
Afslutningsvis er den maksimale værdi, som funktionen tager i opløsningsområdet, 2 og forekommer ved grænsen for opløsningsområdet for værdierne (x = 0, y = 1) og (x = 0, y = -1 ).
Referencer
- Avriel, M. 2003. Ikke-lineær programmering. Dover Publishing.
- Bazaraa. 1979. Ikke-lineær programmering. John Wiley & Sons.
- Bertsekas, D. 1999. Ikke-lineær programmering: 2. udgave. Athena Scientific.
- Nocedal, J. 1999. Numerisk optimering. Springer-Verlag.
- Wikipedia. Ikke-lineær programmering. Gendannet fra: es.wikipedia.com



Endnu ingen kommentarer