
Lås egenskab ved algebra-bevis, eksempler
Det låse ejendom af algebra er et fænomen, der relaterer to elementer i et sæt med en operation, hvor den nødvendige betingelse er, at resultatet, efter at de 2 elementer er behandlet under nævnte operation, også hører til det oprindelige sæt.
For eksempel, hvis lige tal tages som et sæt og en sum som en operation, opnår vi en lås af dette sæt i forhold til summen. Dette skyldes, at summen af 2 lige tal altid giver et andet lige antal og således opfylder låsebetingelsen.

Artikelindeks
- 1 Funktioner
- 2 Antal algebra
- 3 Demo
- 3.1 Sum
- 3.2 Multiplikation
- 4 Særlige tilfælde i R
- 4.1 Opdeling
- 4.2 Arkivering
- 4.3 Logaritme
- 5 eksempler
- 5.1 Sum i N
- 5.2 Subtraktion i N
- 6 Foreslåede øvelser
- 7 Referencer
Egenskaber
Der er mange egenskaber, der bestemmer algebraiske rum eller kroppe, såsom strukturer eller ringe. Låsejendommen er dog en af de mest kendte inden for grundlæggende algebra.
Ikke alle anvendelser af disse egenskaber er baseret på numeriske elementer eller fænomener. Mange hverdagseksempler kan arbejdes ud fra en ren algebraisk-teoretisk tilgang.
Et eksempel kan være borgerne i et land, der påtager sig et juridisk forhold af enhver art, såsom et kommercielt partnerskab eller ægteskab blandt andre. Efter denne operation eller ledelse er udført, forbliver de statsborgere i landet. På denne måde repræsenterer statsborgerskab og ledelse med hensyn til to borgere en lås.
Numerisk algebra
Med hensyn til tal er der mange aspekter, der har været genstand for undersøgelse i forskellige strømme af matematik og algebra. Et stort antal aksiomer og sætninger er kommet frem fra disse undersøgelser, der tjener som det teoretiske grundlag for nutidig forskning og arbejde..
Hvis vi arbejder med de numeriske sæt, kan vi etablere en anden gyldig definition for låsegenskaben. Et sæt A siges at være låsen til et andet sæt B, hvis A er det mindste sæt, der indeholder alle de sæt og operationer, som B huser..
Demonstration
Låsesikkerheden anvendes til elementer og operationer, der er til stede i sættet med reelle tal R.
Lad A og B være to tal, der hører til sættet R, lukningen af disse elementer er defineret for hver operation indeholdt i R.
Sum
- Summen: ∀ A ˄ B ∈ R → A + B = C ∈ R
Dette er den algebraiske måde at sige det på For alle A og B, der hører til de reelle tal, har vi, at summen af A plus B er lig med C, som også hører til de reelle tal.
Det er let at kontrollere, om denne opfattelse er sand; det er nok at udføre summen mellem ethvert reelt tal og kontrollere, om resultatet også hører til de reelle tal.
3 + 2 = 5 ∈ R
-2 + (-7) = -9 ∈ R
-3 + 1/3 = -8/3 ∈ R
5/2 + (-2/3) = 11/6 ∈ R
Det bemærkes, at låsebetingelsen er opfyldt for de reelle tal og summen. På denne måde kan det konkluderes: Summen af reelle tal er en algebraisk lås.
Multiplikation
- Multiplikation: ∀ A ˄ B ∈ R → A. B = C ∈ R
For alle A og B, der hører til realerne, har vi, at multiplikationen af A med B er lig med C, som også hører til realerne.
Ved kontrol med de samme elementer i det foregående eksempel observeres følgende resultater.
3 x 2 = 6 ∈ R
-2 x (-7) = 14 ∈ R
-3 x 1/3 = -1 ∈ R
5/2 x (-2/3) = -5/3 ∈ R
Dette er tilstrækkeligt bevis til at konkludere, at: Multiplikation af reelle tal er en algebraisk lås.
Denne definition kan udvides til alle operationer på reelle tal, skønt vi finder visse undtagelser.

Særlige tilfælde i R
Division
Som det første særlige tilfælde observeres delingen, hvor følgende undtagelse overholdes:
∀ A ˄ B ∈ R → A / B ∉ R ↔ B = 0
For alle A og B, der hører til R vi har, at A blandt B ikke hører til realerne, hvis og kun hvis B er lig med nul.
Denne sag henviser til begrænsningen af ikke at være i stand til at dele med nul. Da nul hører til de reelle tal, konkluderes det, at: lOpdelingen er ikke en lås på realen.
Arkivering
Der er også forstærkningsoperationer, mere specifikt de af radikalisering, hvor der præsenteres undtagelser for radikale beføjelser med lige indeks:
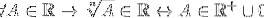
For alle A, der tilhører realerne, tilhører den nte rod af A realerne, hvis og kun hvis A tilhører de positive realer, der er forbundet med et sæt, hvis eneste element er nul.
På denne måde betegnes det, at de jævne rødder kun gælder for positive realer, og det konkluderes, at potentiering ikke er en lås i R.
Logaritme
På en homolog måde kan det ses for den logaritmiske funktion, som ikke er defineret for værdier mindre end eller lig med nul. For at kontrollere, om logaritmen er en lås på R, skal du gøre som følger:
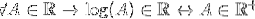
For alle A, der hører til realerne, tilhører A's logaritme til realerne, hvis og kun hvis A tilhører de positive realer.
Ved at udelukke negative værdier og nul, der også hører til R, kan det siges, at:
Logaritmen er ikke en lås af de reelle tal.
Eksempler
Kontroller låsen for tilføjelse og subtraktion af naturlige tal:
Summen i N
Den første ting er at kontrollere låsebetingelsen for forskellige elementer i det givne sæt, hvor hvis det observeres, at ethvert element bryder med tilstanden, kan eksistensen af en lås automatisk nægtes.
Denne egenskab gælder for alle mulige værdier for A og B, som observeret i følgende handlinger:
1 + 3 = 4 ∈ N
5 + 7 = 12 ∈ N
1000 + 10000 = 11000 ∈ N
Der er ingen naturlige værdier, der bryder låsebetingelsen, så det konkluderes:
Summen er en lås i N.
Træk i N
De leder efter naturlige elementer, der er i stand til at bryde tilstanden; A - B tilhører de indfødte.
Betjening er let at finde par af naturlige elementer, der ikke opfylder låsebetingelsen. For eksempel:
7 - 10 = -3 ∉ a N
På denne måde kan vi konkludere, at:
Subtraktion er ikke en lås af sættet med naturlige tal.
Foreslåede øvelser
1-Vis, om låseegenskaben er opfyldt for sættet med rationelle tal Q, for operationens addition, subtraktion, multiplikation og division.
2-Forklar, om sættet med reelle tal er en lås af antallet af heltal.
3-Bestem hvilket numerisk sæt, der kan låse de reelle tal.
4-Bevis låsegenskaben for sættet af imaginære tal med hensyn til addition, subtraktion, multiplikation og division.
Referencer
- Panorama over ren matematik: Bourbakists valg. Jean Dieudonné. Reverte, 1987.
- Algebraisk talteori. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. National Autonomous University of Mexico, 1975.
- Lineær algebra og dets applikationer. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
- Algebraiske strukturer V: kropsteori. Hector A. Merklen. Organisation of American States, Generalsekretariat, 1979.
- Introduktion til kommutativ algebra. Michael Francis Atiyah, I. G. MacDonald. Reverte, 1973.


Endnu ingen kommentarer