Det egenskaber ved lighed henviser til forholdet mellem to matematiske objekter, uanset om de er tal eller variabler. Det er betegnet med symbolet "=", som altid går midt i disse to objekter. Dette udtryk bruges til at fastslå, at to matematiske objekter repræsenterer det samme objekt; i et andet ord, at to objekter er den samme ting.
Der er tilfælde, hvor det er trivielt at bruge lighed. For eksempel er det klart, at 2 = 2. Men når det kommer til variabler, er det ikke længere trivielt og har specifikke anvendelser. For eksempel, hvis vi har det y = x og på den anden side x = 7, kan vi også konkludere, at y = 7.
Ovenstående eksempel er baseret på en af egenskaberne ved lighed, som du snart vil se. Disse egenskaber er vigtige for at løse ligninger (ligestillinger, der involverer variabler), som udgør en meget vigtig del i matematik..
Artikelindeks
Den refleksive egenskab, i tilfælde af lighed, siger, at hvert tal er lig med sig selv og udtrykkes som b = b for ethvert reelt tal b.
I det særlige tilfælde af lighed synes denne egenskab at være indlysende, men i andre typer forhold mellem tal er det ikke. Med andre ord opfylder ikke alle forhold mellem reelt tal denne egenskab. For eksempel et sådant tilfælde af forholdet "mindre end" (<); ningún número es menor que sí mismo.
Den symmetriske egenskab for lighed siger, at hvis a = b, så b = a. Det betyder ikke noget om rækkefølgen i variablerne, den bevares af ligestillingsforholdet.
En vis analogi af denne egenskab med kommutativ egenskab kan observeres i tilfælde af tilføjelse. På grund af denne egenskab svarer det f.eks. Til at skrive y = 4 eller 4 = y.
Den transitive egenskab ved lighed siger, at hvis a = b og b = c, så a = c. For eksempel 2 + 7 = 9 og 9 = 6 + 3; derfor har vi den transitive egenskab, at 2 + 7 = 6 + 3.
En simpel applikation er følgende: antag, at Julian er 14 år, og at Mario er i samme alder som Rosa. Hvis Rosa er i samme alder som Julian, hvor gammel er Mario?
Bag dette scenario bruges den transitive egenskab to gange. Matematisk fortolkes det således: lad “a” være Mario-alderen, “b” Rosa-alderen og “c” Julians alder. Det vides, at b = c og at c = 14.
Ved den transitive egenskab har vi, at b = 14; Rosa er 14 år gammel. Da a = b og b = 14, ved at bruge den transitive egenskab igen, har vi, at a = 14; det vil sige, Mario's alder er også 14 år gammel.
Den ensartede egenskab er, at hvis begge sider af en ligestilling tilføjes eller ganges med det samme beløb, bevares ligestillingen. For eksempel, hvis 2 = 2, så er 2 + 3 = 2 + 3, hvilket er klart, da 5 = 5. Denne egenskab er mest nyttig, når man prøver at løse en ligning.
Antag for eksempel, at du bliver bedt om at løse ligningen x-2 = 1. Det er praktisk at huske, at løsning af en ligning består i eksplicit at bestemme variablen (eller variablerne), der er involveret, baseret på et bestemt tal eller en tidligere specificeret variabel..
At gå tilbage til ligningen x-2 = 1, hvad du skal gøre er at finde eksplicit, hvor meget x er værd. For dette skal variablen ryddes.
Det er forkert blevet undervist, at i dette tilfælde, da tallet 2 er negativt, går det til den anden side af ligestillingen med et positivt tegn. Men det er ikke korrekt at sige det på den måde.
Dybest set er det, du laver, at anvende den ensartede ejendom, som vi vil se nedenfor. Ideen er at rydde "x"; lad det være alene på den ene side af ligningen. Ved konvention er det normalt på venstre side.
Til dette formål er antallet, der skal "eliminere" -2. Måden at gøre det på ville være ved at tilføje 2, da -2 + 2 = 0 og x + 0 = 0. For at være i stand til at gøre dette uden at ændre ligestillingen, skal den samme operation anvendes på den anden side.
Dette gør det muligt at realisere den ensartede egenskab: Da x-2 = 1, hvis tallet 2 tilføjes på begge sider af ligestillingen, siger den ensartede egenskab, at det ikke ændres. Så har vi det x-2 + 2 = 1 + 2, hvilket svarer til at sige at x = 3. Med dette ville ligningen blive løst.
Tilsvarende, hvis du vil løse ligningen (1/5) y-1 = 9, kan du fortsætte med at bruge den ensartede egenskab som følger:
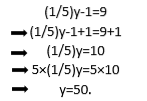
Mere generelt kan følgende udsagn komme:
- Hvis a-b = c-b, så a = c.
- Hvis x-b = y, så x = y + b.
- Hvis (1 / a) z = b, så z = a ×
- Hvis (1 / c) a = (1 / c) b, så a = b.
Annulleringsegenskaben er et bestemt tilfælde af den ensartede ejendom, idet der især tages hensyn til subtraktion og opdeling (som i grunden også svarer til addition og multiplikation). Denne egenskab behandler denne sag separat.
For eksempel, hvis 7 + 2 = 9, så 7 = 9-2. Eller hvis 2y = 6, så y = 3 (divideret med to på begge sider).
Analogt med den foregående sag kan følgende erklæringer gennem annulleringsegenskaberne fastlægges:
- Hvis a + b = c + b, så a = c.
- Hvis x + b = y, så x = y-b.
- Hvis az = b, så er z = b / a.
- Hvis ca = cb, så er a = b.
Hvis vi kender værdien af et matematisk objekt, angiver substitutionsegenskaben, at denne værdi kan erstattes i enhver ligning eller ethvert udtryk. For eksempel, hvis b = 5 og a = bx, så erstattes værdien af "b" i anden ligestilling, at a = 5x.
Et andet eksempel er følgende: Hvis "m" deler "n" og også "n" deler "m", så skal det have, at m = n.
Faktisk at sige, at "m" deler "n" (eller ækvivalent, at "m" er en skiller af "n") betyder, at divisionen m ÷ n er nøjagtig; at dividere "m" med "n" giver et helt tal, ikke et decimal. Dette kan udtrykkes ved at sige, at der findes et heltal "k", således at m = k × n.
Da "n" også deler "m", findes der et heltal "p" således at n = p × m. På grund af substitutionsegenskaben har vi, at n = p × k × n, og for at dette kan ske, er der to muligheder: n = 0, i hvilket tilfælde vi ville have identiteten 0 = 0; eller p × k = 1, derfor identiteten n = n.
Antag at "n" ikke er nul. Så nødvendigvis p × k = 1; derfor er p = 1 og k = 1. Brug af substitutionsegenskaben igen, når vi erstatter k = 1 i ligestillelsen m = k × n (eller ækvivalent, p = 1 i n = p × m) opnår vi endelig, at m = n, hvilket var det, vi ønskede at demonstrere.
Ligesom tidligere blev det set, at hvis en operation som en tilføjelse, multiplikation, subtraktion eller division udføres i begge termer af en lighed, bevares den, på samme måde kan andre operationer, der ikke ændrer en lighed, anvendes.
Nøglen er altid at udføre den på begge sider af ligestillingen og på forhånd sørge for, at operationen kan udføres. Sådan er empowerment; det vil sige, at hvis begge sider af en ligning hæves til den samme magt, har vi stadig en lighed.
For eksempel, da 3 = 3, så 3to= 3to (9 = 9). Generelt givet et heltal "n", hvis x = y, så xn= ogn.
Dette er et særligt tilfælde af empowerment og anvendes, når magten er et ikke-heltal rationelt tal, såsom ½, som repræsenterer kvadratroden. Denne egenskab siger, at hvis den samme rod anvendes på begge sider af en lighed (når det er muligt), bevares ligheden.
I modsætning til det foregående tilfælde skal der udvises forsigtighed med pariteten af den rod, der skal anvendes, da det er velkendt, at den lige rod af et negativt tal ikke er veldefineret.
I tilfælde af at radikalen er jævn, er der ikke noget problem. For eksempel, hvis x3= -8, selvom det er ligestilling, kan du f.eks. Ikke anvende en kvadratrode på begge sider. Men hvis du kan anvende en terningrod (hvilket er endnu mere praktisk, hvis du eksplicit vil kende værdien af x), og derved få det x = -2.
Endnu ingen kommentarer