Det forbindelse eller multipel proportionalitet Det er forholdet mellem mere end to størrelser, hvor direkte og invers proportionalitet kan observeres mellem dataene og det ukendte. Dette er en mere avanceret version af enkel proportionalitet, selvom de teknikker, der anvendes i begge procedurer, er ens..
For eksempel, hvis der er brug for 7 personer til at losse 10 tons merchandise på 3 timer, kan sammensat proportionalitet bruges til at beregne, hvor mange mennesker det vil tage at losse 15 tons på 4 timer..
For at besvare dette spørgsmål er det praktisk at lave en tabel over værdier, der skal studeres og relateres til størrelser og ukendte.
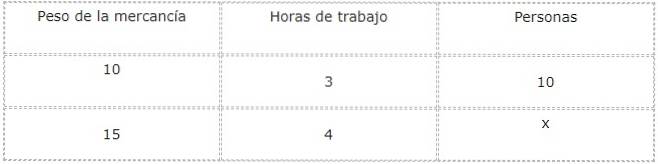
Vi analyserer de typer forhold mellem hver størrelse og den nuværende ukendte, hvilket i dette tilfælde svarer til antallet af mennesker, der vil arbejde.
Når varens vægt stiger, øges også antallet af personer, der kræves for at aflæsse det. På grund af dette er forholdet mellem vægt og arbejdstagere direkte.
På den anden side, når antallet af arbejdstagere stiger, falder arbejdstiden. På grund af dette er forholdet mellem mennesker og arbejdstid af den omvendte type.
Artikelindeks
For at løse eksempler som den ovenfor bruges metoden med sammensat regel af tre for det meste. Dette består i at etablere typerne af forhold mellem størrelser og ukendte og derefter repræsentere et produkt mellem fraktioner.
Med hensyn til det indledende eksempel er brøkene, der svarer til værditabellen, organiseret som følger:
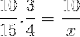
Men inden man løser og løser det ukendte, skal de fraktioner, der svarer til det omvendte forhold, vendes. Hvilket i dette tilfælde svarer til den variable tid. På denne måde vil den operation, der skal løses, være:
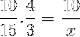
Hvis eneste forskel er inversionen af fraktionen svarende til tidsvariablen 4/3. Vi fortsætter med at betjene og rydde værdien af x.
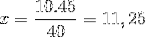
Således er der behov for mere end elleve mennesker for at være i stand til at losse 15 tons merchandise på 4 timer eller mindre.
Proportionalitet er det konstante forhold mellem størrelser, der kan ændres, hvilket vil være symmetrisk for hver af de involverede størrelser. Der er direkte og omvendt forholdsmæssige forhold og definerer således parametrene for enkel eller sammensat proportionalitet.
Den består af et forhold mellem variabler, der viser den samme adfærd, når de ændres. Det er meget hyppigt i beregningen af procentdele, der henviser til andre størrelser end hundrede, hvor dens grundlæggende struktur værdsættes.
Som et eksempel kan der beregnes 15% af 63. Ved første øjekast kan denne procentdel ikke let forstås. Men ved at implementere reglen om tre kan følgende forhold laves: hvis 100% er 63, så 15%, hvor meget vil der være?
100% - 63
15% -X
Og den tilsvarende operation er:
(15%. 63) / 100% = 9,45
Hvor procenttegnene forenkles, og tallet 9.45 opnås, hvilket repræsenterer 15% af 63.
Som navnet antyder, er forholdet mellem variablerne i dette tilfælde det modsatte. Det omvendte forhold skal etableres, inden beregningen fortsættes. Dens procedure er homolog med proceduren for den direkte regel på tre, bortset fra investeringen i den brøk, der skal beregnes..
For eksempel har 3 malere brug for 5 timer til at færdiggøre en væg. Om hvor mange timer ville 4 malere afslutte det?
I dette tilfælde er forholdet omvendt, da arbejdstiden skal falde, når antallet af malere øges. Forholdet er etableret;
3 malere - 5 timer
4 malere - X timer
Når forholdet vendes, vendes rækkefølgen for operationen. Dette er den rigtige måde;
(3 malere). (5 timer) / 4 malere = 3,75 timer
Udtrykket malere er forenklet, og resultatet er 3,75 timer.
For at være i nærværelse af en forbindelse eller multipel proportionalitet er det nødvendigt at finde begge typer forhold mellem størrelsesorden og variabler.
- Direkte: Variablen har samme adfærd som den ukendte. Det vil sige, når den ene øges eller falder, ændres den anden ens.
- Omvendt: Variablen viser en antonymadfærd i forhold til det ukendte. Den brøk, der definerer variablen i værditabellen, skal vendes inverteret for at repræsentere det omvendte proportionelle forhold mellem variabel og ukendt..
Det er meget almindeligt at forveksle størrelsesordenen, når man arbejder med sammensatte proportionaliteter, i modsætning til hvad der sker i de sædvanlige proportionberegninger, hvis natur for det meste er direkte og kan løses ved hjælp af en simpel regel på tre..
Af denne grund er det vigtigt at undersøge den logiske rækkefølge af resultaterne og kontrollere sammenhængen mellem de tal, der er produceret af reglen om tre sammensatte.
I det indledende eksempel ville det at gøre en sådan fejl resultere i 20 som resultatet. Det vil sige 20 mennesker til at aflæsse 15 tons merchandise på 4 timer.
Ved første øjekast ser det ikke ud som et vanvittigt resultat, men det er underligt en stigning på næsten 200% i personale (fra 7 til 20 personer), når stigningen i merchandise er 50%, og endda med en større tidsrum til at udføre arbejdet.
På denne måde repræsenterer den logiske verifikation af resultaterne et vigtigt skridt, når man implementerer reglen om tre forbindelser..
Selvom det er mere grundlæggende i forhold til matematisk træning, er clearingen et vigtigt skridt i tilfælde af proportionalitet. En forkert godkendelse er nok til at ugyldiggøre ethvert resultat opnået i den enkle eller sammensatte regel på tre..
Reglen om tre blev kendt i Vesten gennem araberne med publikationer af forskellige forfattere. Blandt dem Al-Jwarizmi og Al-Biruni.
Takket være sin multikulturelle viden havde Al-Biruni adgang til enorme oplysninger om denne praksis på sine rejser til Indien, idet han var ansvarlig for den mest omfattende dokumentation om reglen om tre.
Han argumenterer i sin forskning for, at Indien var det første sted, hvor brugen af reglen om tre blev almindelig. Forfatteren forsikrer, at den blev udført på en flydende måde i dens direkte, inverse og endda sammensatte versioner..
Den nøjagtige dato, hvor reglen om tre blev en del af den matematiske viden om Indien, er stadig ukendt. Imidlertid blev det ældste dokument, der adresserede denne praksis, Bakhshali-manuskriptet, opdaget i 1881. Det er i øjeblikket i Oxford.
Mange matematikhistorikere hævder, at dette manuskript stammer fra begyndelsen af den nuværende æra..
Et flyselskab skal have 1.535 mennesker. Det vides, at det med 3 fly ville tage 12 dage at få den sidste passager til destinationen. 450 flere mennesker er ankommet til flyselskabet, og 2 fly er beordret til at blive repareret for at hjælpe med denne opgave. Hvor mange dage vil det tage flyselskabet at overføre den sidste passager til deres destination?
Forholdet mellem antallet af mennesker og arbejdsdage er direkte, fordi jo større antal mennesker, jo flere dage vil det tage at udføre dette arbejde..
På den anden side er forholdet mellem fly og dage omvendt proportionalt. Efterhånden som antallet af fly stiger, falder de dage, der er nødvendige for at overføre alle passagerer.
Tabellen over værdier, der henviser til denne sag, er lavet.
Som beskrevet i det indledende eksempel skal tælleren og nævneren vendes om i den brøk svarende til den inverse variabel i forhold til det ukendte. Operationen er som følger:
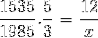
X = 71460/7675 = 9,31 dage
Det tager mere end 9 dage at overføre 1985-personer ved hjælp af 5 fly.
En 25-ton majsafgrøde føres til lastbilerne. Det vides, at det sidste år tog dem 8 timer med en lønningsliste på 150 arbejdere. Hvis lønningslisten for dette år steg med 35%, hvor lang tid tager det at fylde lastbiler med en 40 ton høst??
Inden repræsentationen af værditabellen skal antallet af arbejdere for dette år defineres. Dette steg med 35% fra det oprindelige tal på 150 arbejdere. Til dette anvendes en direkte regel på tre.
100% - 150
35% - X
X = (35.100) / 100 = 52,5. Dette er antallet af yderligere arbejdstagere i forhold til det foregående år, der opnår et samlet antal arbejdere på 203 efter afrunding af det opnåede beløb.
Vi fortsætter med at definere den tilsvarende datatabel
I dette tilfælde repræsenterer vægten en variabel, der er direkte relateret til den ukendte tid. På den anden side har arbejdstagernes variabel et omvendt forhold til tiden. Jo større antal arbejdere, jo kortere arbejdsdag.
Under hensyntagen til disse overvejelser og invertering af den brøk svarende til arbejdstagernes variabel fortsætter vi med at beregne.
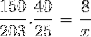
X = 40600/6000 = 6,76 timer
Dagen tager lige under 7 timer.
- Definer 73% af 2875.
- Beregn antallet af timer, Teresa sover, hvis det vides, at hun kun sover 7% af det samlede antal for dagen. Definer, hvor mange timer du sover om ugen.
- En avis udgiver 2000 eksemplarer hver 5. time og bruger kun 2 trykmaskiner. Hvor mange eksemplarer producerer han i løbet af 1 time, hvis han bruger 7 maskiner? Hvor lang tid tager det 10.000 eksemplarer ved hjælp af 4 maskiner?
Endnu ingen kommentarer