
Geometrisk optik hvad det studerer, love, applikationer, øvelser

Det geometrisk optik er den gren af fysik, der fokuserer på at studere den måde, hvorpå lys spreder sig og reflekteres, når det passerer fra et medium til et andet uden at tage hensyn til virkningerne af diffraktion.
På denne måde repræsenteres lys geometrisk af stråler, imaginære linjer vinkelret på lysbølgefronterne..
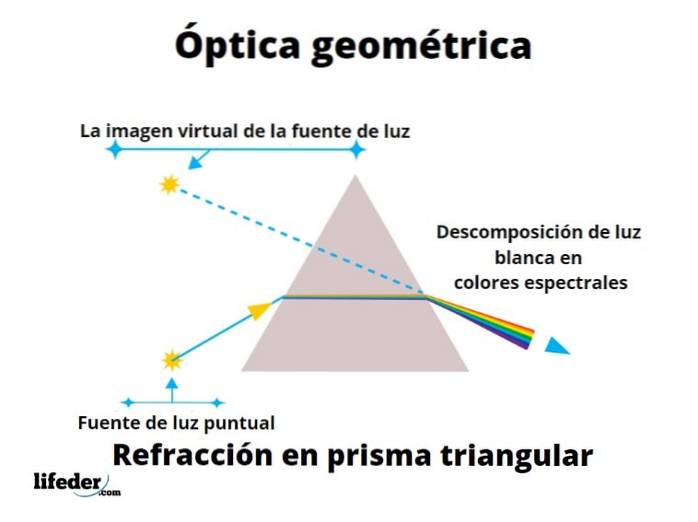
Lysstråler kommer fra lyskilder som solen, en flamme eller en pære, der spredes i alle retninger. Overflader reflekterer delvist disse lysstråler, og det er derfor, vi kan se dem takket være, at øjnene indeholder lysfølsomme elementer.
Takket være strålebehandlingen tager geometrisk optik ikke så meget hensyn til lysets bølgeformer, men forklarer snarere, hvordan billeder dannes i øjet, spejle og projektorer, hvor de gør det, og hvordan de vises.
De grundlæggende principper for geometrisk optik er reflektion og refraktion af lys. Lysstråler strejker i visse vinkler på overfladerne, de møder, og takket være dette hjælper en enkel geometri med at holde styr på deres bane i hvert medium.
Dette forklarer hverdagslige ting som at se på vores billede i badeværelsesspejlet, se en teskefuld, der ser ud til at bøje sig inde i et glas fuld af vand eller forbedre synet med ordentlige briller..
Vi har brug for lys til at forholde os til miljøet, det er grunden til, at dets adfærd altid har forbløffet observatører, der undrede sig over dets natur..
Artikelindeks
- 1 Hvad studerer geometrisk optik? (Studieobjekt)
- 2 Grundlæggende begreber i geometrisk optik
- 2.1 Brydningsindeks
- 2.2 Optisk sti
- 3 love om geometrisk optik
- 3.1 Fermats princip
- 3.2 Refleksionslov
- 3.3 Snells lov
- 4 applikationer
- 4.1 Spejle og linser
- 4.2 Optiske instrumenter
- 4.3 Optisk fiber
- 5 Øvelse løst
- 5.1 Løsning
- 6 Referencer
Hvad studerer geometrisk optik? (Studieobjekt)
Geometrisk optik studerer udbredelsen af lys i et vakuum og i forskellige medier uden at forklare, hvad dets sande natur består af. Til dette gør det brug af strålemodellen og den enkle geometri.
En stråle er den sti, som lys følger i et bestemt gennemsigtigt medium, hvilket er en fremragende tilnærmelse, så længe bølgelængden er lille sammenlignet med størrelsen på objekter..
Dette er tilfældet i mange daglige tilfælde, som dem der blev nævnt i starten..
Der er to grundlæggende præmisser for geometrisk optik:
-Lyset formeres på en retlinet måde.
-Mens den formerer sig gennem forskellige medier, gør lys det efter empiriske love, dvs. opnået ved eksperimentering.
Grundlæggende begreber i geometrisk optik
Brydningsindeks
Lysets hastighed i et materialemedium er forskellig fra et vakuum. Der ved vi, at det er 300.000 km / s, men i luften er det bare lidt lavere og endnu mere i vand eller glas..
Brydningsindeks er en dimensionsløs størrelse, der defineres som kvotienten mellem den hastighed, hvormed lys bevæger sig i vakuum celler og hastighed c i nævnte medium:
n = celler / c
Optisk sti

Det er produktet mellem afstanden med lys, der går fra et punkt til et andet, og mediets brydningsindeks:
L = s. n
Hvor L er den optiske sti, er s afstanden mellem de to punkter, og n repræsenterer brydningsindekset under forudsætning af konstant.
Ved hjælp af den optiske sti sammenlignes lysstråler, der bevæger sig i forskellige medier.
Indfaldsvinkel
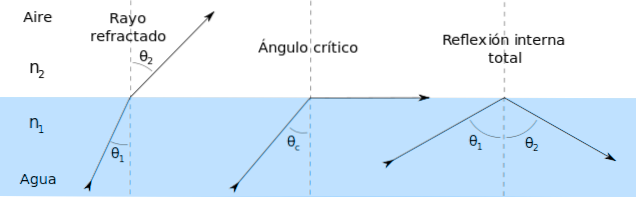
Det er den vinkel, som lysstrålen danner med den normale linje til en overflade, der adskiller to medier.
Loven om geometrisk optik
Fermats princip
Den franske matematiker Pierre de Fermat (1601-1665) bemærkede, at:
Når en lysstråle bevæger sig mellem to punkter, følger den stien, hvor det tager mindst mulig tid.
Og da lys bevæger sig med konstant hastighed, skal dets sti være retlinet.
Med andre ord siger Fermats princip, at lysstrålens sti er sådan, at den optiske sti mellem to punkter er minimal..
Lov om refleksion
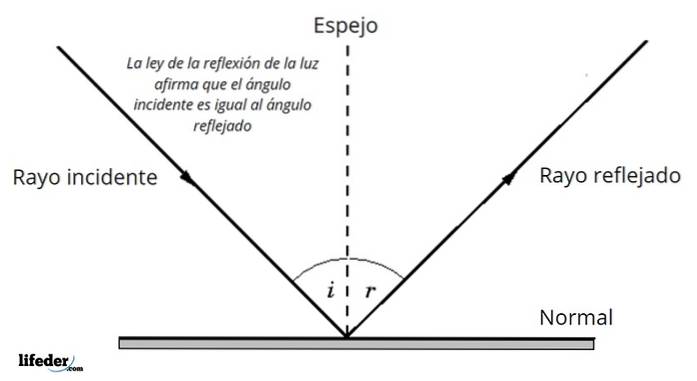
Når man rammer overfladen, der adskiller to forskellige medier, reflekteres en del af den indfaldende stråle - eller det hele - tilbage og gør det med den samme målte vinkel i forhold til det normale til overfladen, som den ramte..

Med andre ord er indfaldsvinklen lig med refleksionsvinklen:
θjeg = θjeg '
Snells lov
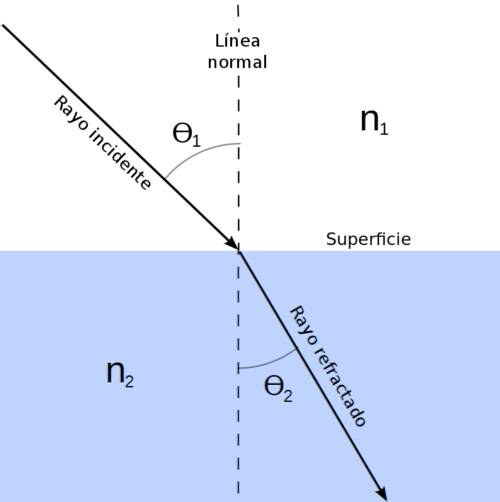
Den hollandske matematiker Willebrord Snell (1580-1626) observerede omhyggeligt lysets opførsel, når det passerer fra luft til vand og glas.
Han så, at når en lysstråle falder på overfladen, der adskiller to medier og danner en bestemt vinkel med den, reflekteres den ene del af strålen tilbage mod det første medium, og den anden fortsætter sin vej gennem det andet..
Således udledte han følgende forhold mellem begge medier:
n1 ⋅ sen θ1 = n2 ⋅ sen θto
Hvor1 og nto er de respektive brydningsindeks, mens θ1 Y θto er indfalds- og brydningsvinklerne målt i forhold til det normale til overfladen ifølge figuren ovenfor.
Ansøgninger
Spejle og linser

Spejle er meget polerede overflader, der reflekterer lys fra genstande, så billeder kan dannes. Flade spejle, som f.eks. På badeværelset eller i en pung, er almindelige.
En linse består af en optisk enhed med to meget tætte brydningsflader. Når en stråle af parallelle stråler passerer gennem en konvergerende linse, konvergerer de på et punkt og danner et billede. Når det kommer til en divergerende linse, sker det modsatte: strålestrålene divergerer på et punkt.
Linser bruges ofte til at rette brydningsfejl i øjet såvel som i forskellige optiske forstørrelsesinstrumenter..
Optiske instrumenter
Der er optiske instrumenter, der gør det muligt at forstørre billeder, for eksempel mikroskoper, forstørrelsesglas og teleskoper. Der er også dem, der ser over øjenhøjde, som periskoper.
Fotokameraer bruges til at tage og bevare billeder, der indeholder et linsesystem og et optageelement for at gemme det dannede billede..
Fiberoptiske
Det er et langt, tyndt og gennemsigtigt materiale baseret på silica eller plast, der bruges til datatransmission. Det udnytter egenskaben ved total refleksion: når lyset når mediet i en bestemt vinkel, forekommer der ingen brydning, derfor kan strålen bevæge sig lange afstande og hoppe inde i glødetråden.
Træning løst
Objekter i bunden af en pool eller dam ser ud til at være tættere end de faktisk er, hvilket skyldes brydning. I hvilken tilsyneladende dybde ser en observatør en mønt, der er i bunden af en 4 m dyb pool??
Antag, at strålen, der kommer ud af mønten, når observatørens øje i en vinkel på 40 ° i forhold til det normale..
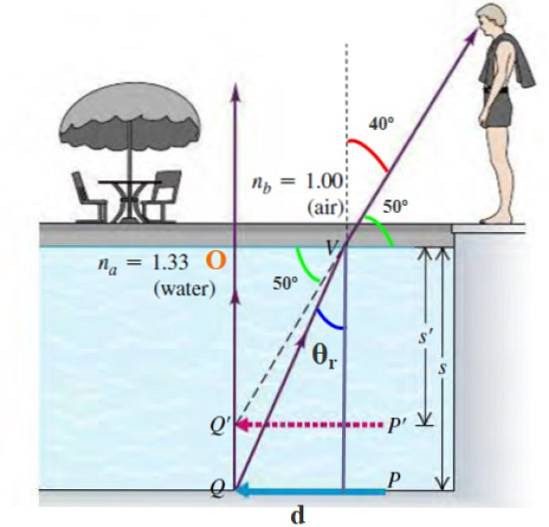
Fakta: brydningsindekset for vand er 1,33, det for luft er 1.
Opløsning
Den tilsyneladende dybde af mønten er s 'og dybden af puljen er s = 4 m. Mønten er ved punkt Q, og observatøren ser den på punkt Q '. Dybden af dette punkt er:
s '= s - Q'Q
Fra Snells lov:
nb ⋅ sin 40º = ntil ⋅ sen θr
sen θr = (nb ⋅ sin 40º) ÷ ntil = sin 40º /1,33 = 0,4833
θr = lysbue (0,4833) = 28,9º
Når vi kender denne vinkel, beregner vi afstanden d = OV fra den højre trekant, hvis skarpe vinkel er θr:
tan 28,9º = OV / 4 m
OV = 4m × tan 28,9º = 2,154 m
På den anden side:
tan 50º = OQ '/ OV
Derfor:
OQ '= OV × tan 50º = 2.154 m × tan 50º = 2.57 m.
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 2. Mc Graw Hill.
- Figueras, M. Geometrisk optik: bølgeløs optik. Åbent universitet i Catalonien.
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 2. 7. Ed. Cengage Learning.
- Tippens, P. 2011. Fysik: begreber og applikationer. 7. udgave. Mcgraw bakke.


Endnu ingen kommentarer