
Coplanar pointligning, eksempel og løste øvelser
Det coplanar punkter de tilhører alle det samme plan. To punkter er altid i samme plan, da disse punkter definerer en linje, gennem hvilken uendelige fly passerer. Derefter hører begge punkter til hvert af flyene, der passerer gennem linjen, og derfor vil de altid være i samme plan.
På den anden side definerer tre punkter et enkelt plan, hvorfra det følger, at tre punkter altid vil være i samme plan som det plan, de bestemmer..
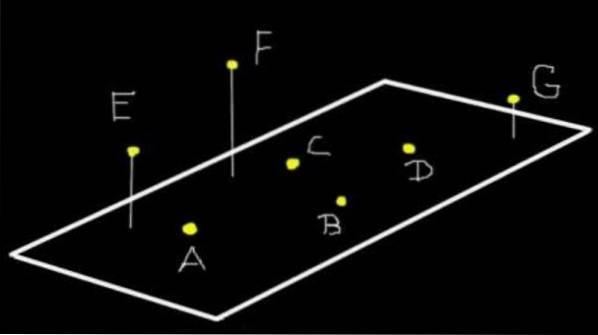
Mere end tre punkter kan være i samme plan eller ikke. For eksempel er figur A, punkterne A, B, C og D i samme plan som (Ω) -planet. Men E, F og G er ikke plan til (Ω), skønt de er i samme plan som det plan, de definerer.
Artikelindeks
- 1 Ligning af et plan givet tre point
- 2 Eksempel
- 2.1 Løsning
- 3 Løst øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 3.3 - Øvelse 3
- 3.4 - Øvelse 4
- 4 Referencer
Ligning af et plan givet tre point
Ligningen af et plan bestemt af tre kendte punkter A, B, C er et matematisk forhold, der garanterer, at ethvert punkt P med generiske koordinater (x, y, z), der opfylder ligningen, hører til nævnte plan.
Den foregående sætning svarer til at sige, at hvis P af koordinater (x, y, z) opfylder ligningen af planet, vil punktet være i samme plan som de tre punkter A, B, C, der bestemte planet.
For at finde ligningen af dette plan, lad os starte med at finde vektorerne AB Y AC:
AB = [Bx - Axe, By - Ay, Bz - Az]
AC = [Cx - Axe, Cy - Ay, Cz - Az]
Vektorproduktet AB x AC resulterer i en vektor vinkelret eller normal på planet bestemt af punkterne A, B, C.
Ethvert punkt P af koordinater (x, y, z) hører til planet, hvis vektoren AP er vinkelret på vektoren AB x AC, hvilket er garanteret, hvis:
AP • (AB x AC) = 0
Dette svarer til at sige, at det tredobbelte produkt af AP, AB Y AC er nul. Ovenstående ligning kan skrives i matrixform:
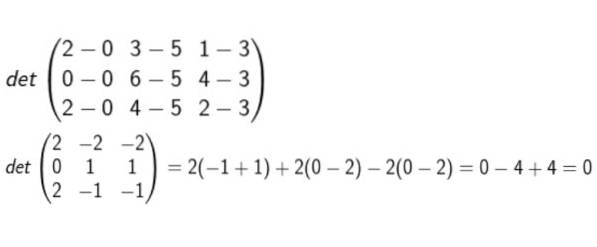
Eksempel
Lad punkterne A (0, 1, 2); B (1, 2, 3); C (7, 2, 1) og D (til, 0, 1). Hvilken værdi skal det have til så de fire punkter er i samme plan?
Opløsning
For at finde værdien af a skal punkt D være en del af planet bestemt af A, B og C, hvilket er garanteret, hvis det opfylder ligningen af planet.
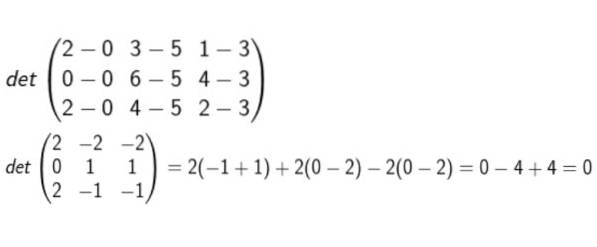
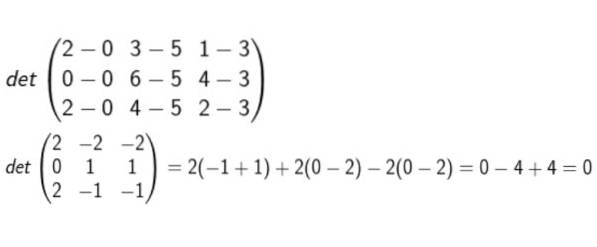
Udvikling af den determinant, vi har:
a (-1-1) + 1 (-1 - 7) -1 (1-7) = -2a -8 + 6 = -2a - 2 = 0
Ovenstående ligning fortæller os det a = -1 så ligestilling bliver opfyldt. Med andre ord, den eneste måde, som punkt D (til, 0,1) er i samme plan som punkterne A, B og C er det til værd -1. Ellers er det ikke ensartet.
Løst øvelser
- Øvelse 1
Et plan skærer de kartesiske akser X, Y, Z ved henholdsvis 1, 2 og 3. Skæringspunktet mellem dette plan og akserne bestemmer punkterne A, B og C. Find komponenten Dz i et punkt D, hvis kartesiske komponenter er:
D (-Dz, Dz + 1, Dz)
Forudsat at D er i samme plan som punkt A, B og C.
Opløsning
Når der er kendt aflytninger af et plan med de kartesiske akser, kan den segmentform af planens ligning bruges:
x / 1 + y / 2 + z / 3 = 1
Da punkt D skal tilhøre det forrige plan, skal det:
-Dz / 1 + (Dz + 1) / 2 + Dz / 3 = 1
Nemlig:
-Dz + Dz / 2 + ½ + Dz / 3 = 1
Dz (-1 + ½ + ⅓) = ½
Dz (-1 / 6⅙) = ½
Dz = -3
Af ovenstående følger, at punkt D (3, -2, -3) er i samme plan som punkterne A (1, 0, 0); B (0, 2, 0) og C (0, 0, 3).
- Øvelse 2
Bestem om punkterne A (0, 5, 3); B (0, 6, 4); C (2, 4, 2) og D (2, 3, 1) er coplanar.
Opløsning
Vi danner matrixen, hvis rækker er koordinaterne for D-A, B-A og C-A. Derefter beregnes determinanten, og det verificeres, om den er nul eller ej.
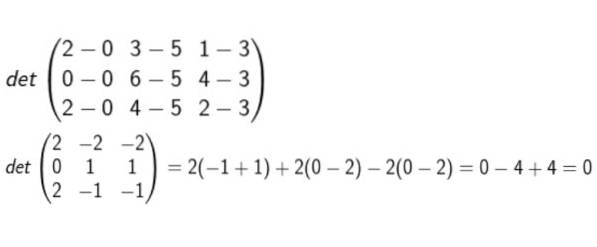
Efter at have udført alle beregningerne konkluderes det, at de er i samme plan.
- Øvelse 3
Der er to linjer i rummet. En af dem er linjen (R), hvis parametriske ligning er:
(R): x = 1 + 2 λ; y = 1 - λ; z = 1
Og den anden er linjen (S), hvis ligning er:
(S): x + 2 y = 1; z = -1
Vis, at (R) og (S) er linieplaner, dvs. de ligger i samme plan.
Opløsning
Lad os starte med vilkårligt at tage to punkter på linjen (R) og to på linjen (S):
Lige (R): λ = 0; A (1, 1, 1) og λ = 1; B (3, 0, 1)
Lad os gøre det x = 0 på linjen (S)=> y = ½; C (0, ½, -1). Og på den anden side, hvis vi gør det y = 0 => x = 1; D (1, 0, -1).
Det vil sige, vi har taget punkterne A og B, der hører til linjen (R) og punkterne C og D, der hører til linjen (S). Hvis disse punkter er i samme plan, vil de to linjer også være i samme plan.
Nu vælger vi punkt A som omdrejningspunkt, og så finder vi vektorernes koordinater AB, AC Y AD. På denne måde får du:
B - A: (3-1, 0 -1, 1 - 1) => AB= (2, -1, 0)
C - A: (0-1, 1/2 -1, -1 - 1) => AC= (-1, -1/2, -2)
D - A: (1-1, 0 -1, -1 - 1) => AD= (0, -1, -2)
Det næste trin er at konstruere og beregne determinanten, hvis første række er vektorens koefficienter AB, anden række er dem af AC og den tredje række af vektoren AD:
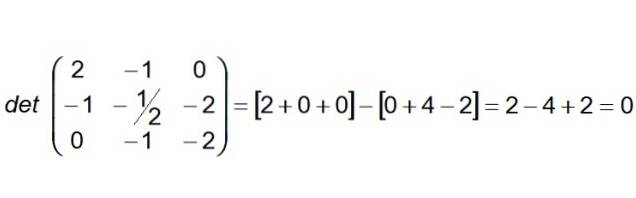
Da determinanten viser sig at være nul, kan vi konkludere, at de fire punkter er i samme plan. Derudover kan det anføres, at linjerne (R) og (S) også er ensartede.
- Øvelse 4
Linjerne (R) og (S) er i samme plan som vist i øvelse 3. Find ligningen af det plan, der indeholder dem.
Opløsning
Punkt A, B, C definerer dette plan fuldstændigt, men vi vil pålægge, at ethvert punkt X af koordinater (x, y, z) hører til det samme.
X - A: (x-1, y -1, z - 1) => ØKSE= (x-1, y -1, z - 1)
B - A: (3-1, 0 -1, 1 - 1) => AB= (2, -1, 0)
C - A: (0-1, 1/2 -1, -1 - 1) => AC= (-1, -1/2, -2)
For at X skal høre til det plan, der er defineret af A, B, C, og hvor linjerne (R) og (S) er indeholdt, er det nødvendigt, at determinanten dannes i sin første række af komponenterne i ØKSE, i det andet af dem af AB og i det tredje af dem af AC:
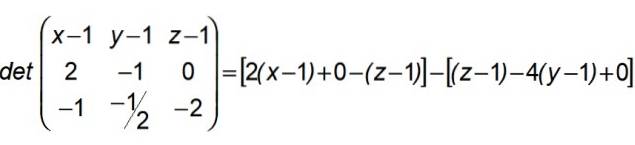
Efter dette resultat grupperer vi på denne måde:
2 (x-1) + 4 (y-1) -2 (z-1) = 0
Og straks ser du, at det kan omskrives sådan:
x - 1 + 2y - 2 - z + 1 = 0
Derfor er x + 2y - z = 2 ligningen af det plan, der indeholder linjerne (R) og (S).
Referencer
- Fleming, W. 1989. Precalculus Mathematics. Prentice Hall PTR.
- Kolman, B. 2006. Lineær algebra. Pearson Uddannelse.
- Leal, J. M. 2005. Plane Analytical Geometry. Mérida - Venezuela: Redaktionel Venezolana C. A.
- Navarro, Rocio. Vektorer. Gendannet fra: books.google.co.ve.
- Pérez, C. D. 2006. Forudberegning. Pearson Uddannelse.
- Prenowitz, W. 2012. Grundlæggende begreber i geometri. Rowman & Littlefield.
- Sullivan, M. 1997. Precalculus. Pearson Uddannelse.


Endnu ingen kommentarer