
Hvad er det magnetiske øjeblik?
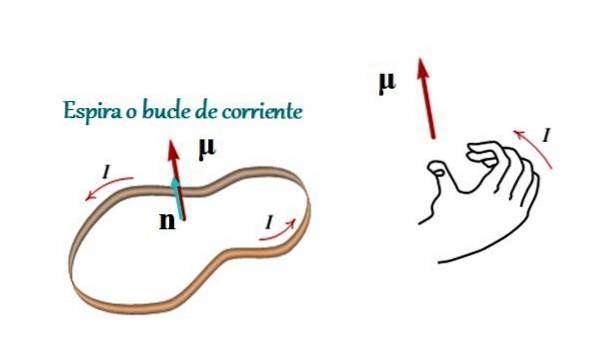
Det magnetisk øjeblik er en vektor, der relaterer strømmen, der passerer gennem en sløjfe eller lukket sløjfe med sit område. Dens modul er lig med produktet af strømens og områdets intensitet, og dets retning og sans er givet ved højre håndsregel, som vist i figur 1.
Denne definition er gyldig uanset formen på sløjfen. Med hensyn til enheden af det magnetiske moment er det i det internationale system for SI-enheder ampere × mto.
I matematiske termer betegner den magnetiske momentvektor med det græske bogstav μ (i fed skrift, fordi det er en vektor og således adskiller sig fra dens størrelse), udtrykkes det som:
μ = AI n
Hvor jeg er intensiteten af strømmen, er A det område, der er omsluttet af sløjfen og n er enhedsvektoren (med et modul svarende til 1), der peger i retningen vinkelret på sløjfens plan, og hvis sans er givet af reglen om højre tommelfinger (se figur 1).
Denne regel er meget enkel: ved at krølle de fire fingre på højre hånd for at følge strømmen angiver tommelfingeren retning og følelse af retning. n og derfor det magnetiske øjebliks.
Ovenstående ligning er gyldig for en sløjfe. Hvis der er N drejninger som i en spole, ganges magnetmomentet med N:
μ = NAI n
Artikelindeks
- 1 Magnetmoment og magnetfelt
- 1.1 Dipolens magnetfelt
- 2 Effekt af et eksternt felt på sløjfen
- 2.1 Moment på en rektangulær løkke
- 2.2 Den magnetiske dipoles potentielle energi
- 3 Referencer
Magnetisk øjeblik og magnetfelt
Det er let at finde udtryk for det magnetiske moment for sving med regelmæssige geometriske former:
-Firkantet sidesving ℓ: μ = Iℓto n
-Rektangulær sidespiral til Y b: μ = Iab n
-Cirkelspiral med radius R: μ = IπRto n
Dipol magnetisk felt
Det magnetiske felt, der produceres af strømkredsen eller strømkredsen, svarer meget til en stangmagnet og også Jordens.
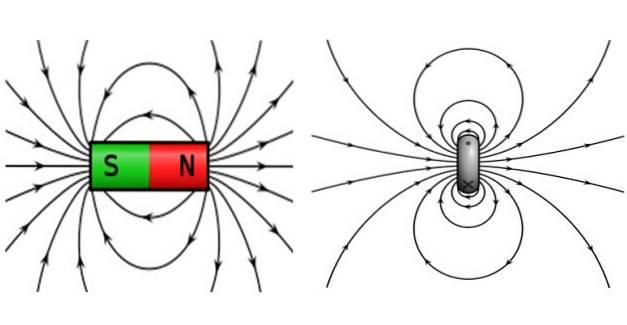
Stangmagneter er kendetegnet ved at have en nordpol og en sydpol, hvor modsatte poler tiltrækker og som poler afviser. Marklinjerne er lukkede, de forlader nordpolen og ankommer til sydpolen.
Nu er de magnetiske poler uadskillelige, hvilket betyder, at hvis du deler en stangmagnet i to mindre magneter, har de stadig deres egne nord- og sydpoler. Det er ikke muligt at have isolerede magnetiske poler, derfor kaldes stangmagneten magnetisk dipol.
Magnetfeltet i en cirkulær sløjfe med radius R, der bærer en strøm I, beregnes ved hjælp af Biot-Savart-loven. For de punkter, der hører til symmetriaksen (i dette tilfælde x-aksen), er feltet givet ved:

Forholdet mellem magnetfeltet og dipolens magnetiske øjeblik
Omfatter det magnetiske øjeblik i det forrige udtryksresultat:

På denne måde er magnetfeltets intensitet proportional med magnetmomentet. Bemærk, at feltintensiteten falder med afstandens terning.
Denne tilnærmelse gælder for enhver løkke, så længe x er stor i forhold til dens dimensioner.
Og da linierne i dette felt er så ens som stregmagnetens, er ligningen en god model for dette magnetfelt og for andre systemer, hvis linjer er ens, såsom:
-Opladede partikler i bevægelse som elektronen.
-Atomet.
-Jorden og andre planeter og satellitter i solsystemet.
-Stjerner.
Effekt af et eksternt felt på sløjfen
En meget vigtig egenskab ved det magnetiske øjeblik er dens forbindelse til det drejningsmoment, som sløjfen oplever i nærvær af et eksternt magnetfelt..
En elektrisk motor indeholder spoler, hvorigennem en strøm i skiftende retning passerer, og som takket være det eksterne felt oplever en roterende effekt. Denne rotation får en akse til at bevæge sig, og den elektriske energi omdannes til mekanisk energi under processen..
Moment på en rektangulær løkke
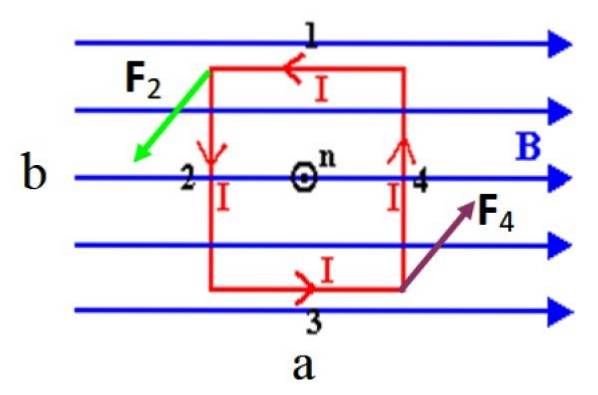
Antag for at gøre det nemmere at beregne en rektangulær løkke med sider til Y b, hvis normale vektor n, rager ud mod skærmen, oprindeligt vinkelret på et ensartet magnetfelt B, som i figur 3. Siderne af sløjfen oplever kræfter givet af:
F = JegL x B
Hvor L er en vektor med størrelsesorden lig med segmentets længde og rettet i henhold til strømmen, I er dens intensitet og B er marken. Kraften er vinkelret på begge dele L hvad marken angår, men ikke alle sider oplever magt.

I den viste figur er der ingen kraft på korte sider 1 og 3, fordi de er parallelle med feltet. Husk at krydsproduktet mellem parallelle vektorer er nul. Imidlertid lange sider 2 og 4, som er vinkelrette på B, opleve de kræfter, der betegnes som Fto Y F4.
Disse kræfter dannes et par: de har samme størrelse og retning, men modsatte retninger, derfor er de ikke i stand til at overføre løkken midt i marken. Men de kan rotere det, da drejningsmomentet τ udøvet af hver kraft i forhold til den lodrette akse, der passerer gennem sløjfens centrum, har samme retning og sans.
I henhold til definitionen af drejningsmoment, hvor r er positionsvektoren:
τ = r x F
Derefter:
τto = τ4=(a / 2) F (+j )
De enkelte drejningsmomenter annulleres ikke, da de har samme retning og sans, så de tilføjes:
τnet = τto + τ4 = a F (+j )
Og som størrelsen af kraften F = IbB, resulterer det:
τnet = I⋅a⋅b⋅B (+j )
Produktet a⋅b er området A på sløjfen, så Iab er størrelsen af det magnetiske øjeblik μ. Derfor τnet = μ⋅B (+j )
Det kan ses, at drejningsmomentet generelt falder sammen med vektorproduktet mellem vektorerne μ Y B:
τnet = μ x B
Og selvom dette udtryk stammer fra en rektangulær sløjfe, er det gyldigt for en flad sløjfe med vilkårlig form.
Effekten af feltet på sløjfen er et drejningsmoment, der har tendens til at justere det magnetiske øjeblik med feltet.
Potentiel energi af den magnetiske dipol
For at dreje løkken eller dipolen midt i marken skal der arbejdes mod den magnetiske kraft, som ændrer dipolens potentielle energi. Variationen af energien ΔU, når drejningen roterer fra vinklen θeller vinklen θ er givet af integralet:

ΔU = -μB cos θ
Hvilket igen kan udtrykkes som punktproduktet mellem vektorerne B Y μ:
ΔU = - μB
Den mindste potentielle energi i dipolen opstår, når cos θ = 1, hvilket betyder, at μ Y B de er parallelle, energien er maksimal, hvis de er modsatte (θ = π), og den er nul, når de er vinkelrette (θ = π / 2).
Referencer
- Figueroa, D. 2005. Serie: Physics for Sciences and Engineering. Bind 5. elektromagnetisme. Redigeret af Douglas Figueroa (USB).
- Resnick, R. 1999. Fysik. Bind 2. 3. udgave på spansk. Compañía Editorial Continental S.A. af C.V.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 2. Pearson.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 2. 7. Ed. Cengage Learning.
- Tipler, P. (2006) Fysik til videnskab og teknologi. 5. udg. Bind 2. Editorial Reverté.
Endnu ingen kommentarer