
Hvad er kapacitiv reaktans, og hvordan beregnes den?
Det kapacitiv reaktans er den modstand, som en kondensator, et reguleringselement af ladestrømmen i et vekselstrømskredsløb, modsætter sig strømens passage.
I et kredsløb, der består af en kondensator og aktiveres af en vekselstrømskilde, kan den kapacitive reaktans X defineresC som følger:
xC = 1 / ωC

Eller også:
xC = 1 / 2πfC
Hvor C er kondensatorkapaciteten, og ω er kildens vinkelfrekvens relateret til frekvensen f ved:
ω = 2πf
Kapacitiv reaktans afhænger af det inverse af frekvensen, derfor ved høje frekvenser har det en tendens til at være lille, mens reaktansen ved lave frekvenser er stor.
Den internationale systemenhed til måling af kapacitiv reaktans er ohm (Ω), forudsat at kondensatorens kapacitans C er i farad, (forkortet F), og frekvensen udtrykkes i inverse sekunder (s-1).
Mens opladningen varer, etableres en skiftevis spænding og strøm gennem kondensatoren, hvis amplituder eller maksimale værdier betegnet henholdsvis som VC og jegC, er forbundet med kapacitiv reaktans analogt med Ohms lov:
VC = JegC ⋅ XC
I en kondensator er spændingen 90º bag strømmen, eller strømmen er 90 ° foran strømmen, som du foretrækker. Under alle omstændigheder er frekvensen den samme.
Når XC er meget stor, strømmen har tendens til at være lille og gør værdien af X tendens til uendeligC, kondensatoren opfører sig som et åbent kredsløb, og strømmen er nul.
Artikelindeks
- 1 Sådan beregnes kapacitiv reaktans
- 1.1 Strøm og spænding over kondensatoren
- 2 Kompleks impedans af kondensator
- 2.1 Impedans af et serie RC kredsløb
- 3 Anvendelser af kapacitiv reaktans
- 4 Referencer
Sådan beregnes kapacitiv reaktans
Lad os se et eksempel på, hvordan man beregner kapacitiv reaktans: antag, at en 6 μF kondensator er forbundet til en stikkontakt på 40 V og frekvens F 60 Hz.
For at finde den kapacitive reaktans anvendes definitionen i starten. Vinkelfrekvensen ω er givet ved:
ω = 2πf = 2π x 60 Hz = 377 s-1
Derefter erstattes dette resultat i definitionen:
xC = 1 / ωC = 1 / (377 s-1x 6 x 10 -6 F) = 442,1 ohm
Lad os nu se amplituden af strømmen, der flyder i kredsløbet. Da kilden tilbyder en spænding med amplitude VC = 40 V, vi bruger forholdet mellem kapacitiv reaktans, strøm og spænding til at beregne amplituden af strømmen eller den maksimale strøm:
jegC = VC / XC = 40 V / 442,1 ohm = 0,09047 A = 90,5 m A..
Hvis frekvensen bliver meget stor, bliver den kapacitive reaktans lille, men hvis frekvensen blev 0, og vi havde en jævnstrøm, ville reaktansen have tendens til at være uendelig..
Strøm og spænding over kondensatoren
Når en kondensator er forbundet til en vekselstrømskilde, når den oscillerer og ændrer dens polaritet, oplever kondensatoren alternative opladninger og afladninger..
For en frekvens på 60 Hz som den i eksemplet er spændingen positiv 60 gange pr. Sekund og negativ yderligere 60 gange pr. Sekund.
Forøgelse af spændingen skubber strømmen en vej, men hvis kondensatoren aflades, produceres der strøm i den modsatte retning, der modsætter den første..
Hvis vC (t) = Vm Når vi ved, at kapaciteten er forholdet mellem belastningen og spændingen, har vi belastningen:
C = q / V → q (t) = CV = CVm sen ωt
Og ved at have belastningen som en funktion af tiden får vi strømmen, som er afledt af det:
jegC(t) = CVm ω cos ωt
Men sinus og cosinus er relateret af: cos α = sin (α + π / 2), derfor:
jegC(t) = CVm ω sin (ωt + π / 2) = IC sin (ωt + π / 2)
Med migC = CVC ω
Som du kan se, er der en forskel på 90º fremadstrømmen i forhold til spændingen, som den blev kommenteret i starten.
I beskrivelsen af denne type kredsløb er begrebet fasor, som er meget lig en vektor og gør det muligt at repræsentere enhver alternerende størrelse såsom strøm, spænding eller impedans i det komplekse plan.
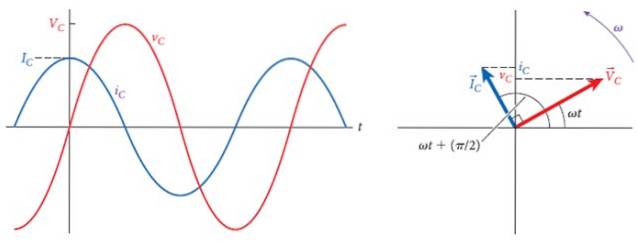
Den følgende figur viser til højre spændings- og strømfaserne i kondensatoren, der danner en vinkel på 90 ° mellem dem, hvilket er faseforskellen mellem de to..
Til venstre er de respektive grafer med forskellige amplituder, men den samme frekvens. Med tiden fører strømmen spændingen, og når den er maksimal, er strømmen nul, og når spændingen er nul, er strømmen maksimal, men med polariteten omvendt.
Kompleks kondensatorimpedans
I et kredsløb med modstande, kondensatorer og induktanser er reaktansen den imaginære del af impedansen Z, en kompleks størrelse, der i vekselstrømskredsløb har en rolle svarende til den elektriske modstand for jævnstrømskredsløb..
Faktisk er impedansen af et kredsløb defineret som forholdet mellem spænding og strøm:
Z = V / I
For en kondensator eller kondensator gives impedansen af kvotienten:
ZC = v (t) / i (t) = VC sin ωt / IC sin (ωt + π / 2)
En måde at udtrykke spænding og strøm på som faser er ved at indikere amplitude og fasevinkel (polær form):
v (t) = VC ∠ 0º
i (t) = IC º 90º
Derfor:
ZC = VC ∠ 0º / IC ∠ 90º = (VC / JegC) ∠ 0º -90º =
= VC / CVC ω ∠ -90º = (1 / ωC) ∠ -90º =
ZC = (- j) XC
Det vil sige, kondensatorens impedans er dens kapacitive reaktans ganget med negativet af den imaginære enhed.
Impedans af et serie RC kredsløb
Impedansen af et vekselstrømskredsløb med modstande, kondensatorer og induktorer kan også repræsenteres binomalt ved:
Z = R + jX
I denne ligning repræsenterer R modstanden, som svarer til den reelle del, j er den imaginære enhed, og X er reaktansen, som kan være kapacitiv eller induktiv eller en kombination af begge, hvis disse elementer er til stede på samme tid i kredsløb.
Hvis kredsløbet indeholder en modstand og en kondensator i serie, er deres impedans:
Z = ZR + ZC
Da spænding og strøm i modstand er i fase, er den resistive impedans simpelthen værdien af modstanden R.
I tilfælde af kapacitiv impedans har vi allerede set, at ZC = -jXC , Derfor er impedansen til RC-kredsløbet:
Z = R - jXC = R - j (1 / ωC)
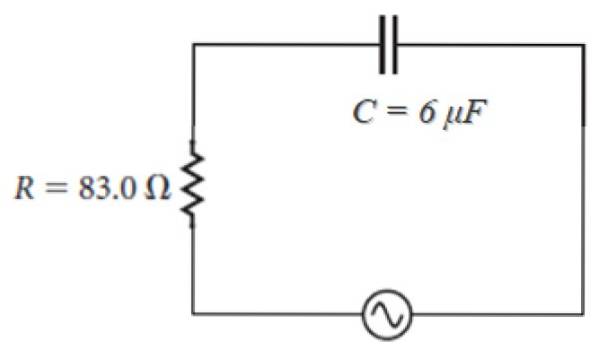
For eksempel i kredsløbet vist nedenfor, hvis kilde er af formen:
100 V ⋅ sin (120πt)
Ved at observere, at ω = 120π, er impedansen:
Z = 83,0 - j [(1 / (120π ⋅ 6 x 10)-6)] ohm = 83,0 - 442,1 j ohm.
Kapacitive reaktansanvendelser
Højpasfiltre, lavpasfiltre, bro-type kredsløb til måling af kapacitanser og induktanser og faseskiftende kredsløb er blandt de vigtigste anvendelser af kredsløb, der indeholder kapacitive reaktanser, i kombination med induktanser og elektriske modstande..
I stereoanlæg kommer nogle højttalere med separate højttalere. bashøjttaler (større) til lave frekvenser og diskant eller lille horn til høje frekvenser. Dette forbedrer ydeevnen og lydkvaliteten.
De bruger kondensatorer, der forhindrer ankomsten af lave frekvenser i tweeter, mens der i wooferen tilføjes en induktor for at undgå højfrekvente signaler, da induktansen har en reaktans, der er proportional med frekvensen: XL = 2πfL.
Referencer
- Alexander, C. 2006. Grundlæggende om elektriske kredsløb. 3. Udgave. Mc Graw Hill.
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 2. Mc Graw Hill.
- Figueroa, D. 2005. Serie: Physics for Sciences and Engineering. Bind 6. elektromagnetisme. Redigeret af Douglas Figueroa (USB).
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Serway, R., Jewett, J. 2008. Fysik til videnskab og teknik. Bind 1. 7. Ed. Cengage Learning.



Endnu ingen kommentarer