
Hvad er coplanar-vektorer? (Med øvelser løst)
Det coplanar vektorer eller coplanar er dem, der er indeholdt i det samme plan. Når der kun er to vektorer, er de altid i samme plan, da der er uendelige plan, er det altid muligt at vælge en, der indeholder dem.
Hvis du har tre eller flere vektorer, kan det være, at nogle af dem ikke er i samme plan som de andre, derfor kunne de ikke betragtes som plan. Den følgende figur viser et sæt coplanære vektorer angivet med fed skrift TIL, B, C Y D:
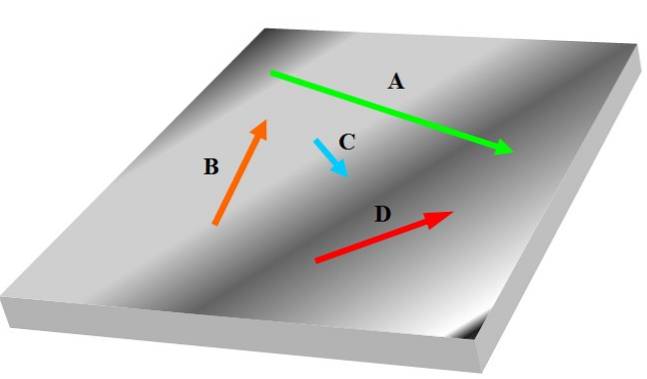
Vektorer er relateret til opførsel og egenskaber af relevante fysiske størrelser inden for videnskab og teknik; for eksempel hastighed, acceleration og kraft.
En kraft frembringer forskellige effekter på et objekt, når den måde, den påføres på varieres, for eksempel ved at ændre intensitet, retning og retning. Selv om kun en af disse parametre ændres, er resultaterne betydeligt forskellige..
I mange anvendelser, både i statik og dynamik, er kræfterne, der virker på en krop, på samme plan, derfor betragtes de som plan.
Artikelindeks
- 1 Betingelser for, at vektorerne skal være i samme plan
- 1.1 Blandet produkt mellem tre vektorer
- 2 applikationer
- 2.1 Coplanar, samtidige og ikke-kollinære kræfter
- 3 Løst øvelser
- 3.1-Øvelse 1
- 3.2-Øvelse 2
- 4 Referencer
Betingelser for, at vektorerne skal være i samme plan
For at tre vektorer skal være i samme plan, skal de ligge på samme plan, og dette sker, hvis de opfylder en af følgende betingelser:
-Vektorer er parallelle, derfor er deres komponenter proportionale og lineært afhængige.
-Dit blandede produkt er nul.
-Hvis du har tre vektorer, og en af dem kan skrives som en lineær kombination af de to andre, er disse vektorer i samme plan. For eksempel er en vektor, der er resultatet af summen af to andre, de tre alle i samme plan.
Alternativt kan coplanaritetsbetingelsen fastlægges som følger:
U V w er coplanar, hvis der er tre (skalære) tal α, β, γ således at αeller + βv + γw = 0 med (α, β, γ) andet end (0, 0, 0)
Blandet produkt mellem tre vektorer
Det blandede produkt mellem vektorer er defineret af tre vektorer eller, v Y w, hvilket resulterer i en skalar, der er resultatet af følgende handling:
eller · (v x w) = eller · (v x w)
For det første udføres krydsproduktet i parentes: v x w, hvis resultat er en normal vektor (vinkelret) på det plan, hvor begge v Hvad w.
Ja eller er på samme plan som v Y w, naturligvis skal det skalære produkt (punktprodukt) mellem u og den normale vektor være 0. På denne måde bekræftes det, at de tre vektorer er i samme plan (de ligger på samme plan).
Når det blandede produkt ikke er nul, er resultatet lig med volumenet af parallelepiped, der har vektorerne eller, v Y w som tilstødende sider.
Ansøgninger
Coplanar, samtidige og ikke-kollinære styrker
Styrkerne samtidig de anvendes alle til det samme punkt. Hvis de også er i samme plan, kan de erstattes af en enkelt, som kaldes resulterende kraft og har samme virkning som de oprindelige kræfter.
Hvis en krop er i ligevægt takket være tre coplanar kræfter, samtidig og ikke kollinær (ikke parallel), kaldet TIL, B Y C, det Lamys sætning påpeger, at forholdet mellem disse kræfter (størrelser) er som følger:
A / sin α = B / sin β = C / sin γ
Med α, β og γ som de modsatte vinkler til de påførte kræfter, som vist i følgende figur:
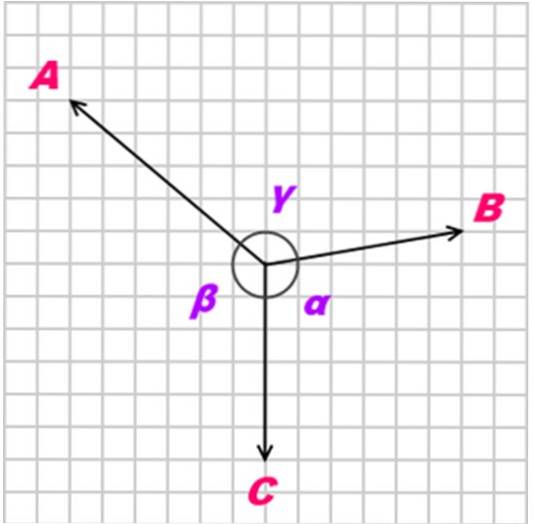
Løst øvelser
-Øvelse 1
Find værdien af k, så følgende vektorer er i samme plan:
eller = <-3, k, 2>
v = <4, 1, 0>
w = <-1, 2, -1>
Opløsning
Da vi har komponenterne i vektorerne, anvendes kriteriet for det blandede produkt, derfor:
eller · (v x w) = 0
Det løses først v x w. Vektorerne udtrykkes i form af enhedsvektorerne jeg, j Y k der skelner mellem de tre vinkelrette retninger i rummet (bredde, højde og dybde):
v= 4 jeg + j + 0 k
w= -1 jeg + toj -1 k
v x w = -4 (i x i) + 8 (i x j) - 4 (i x k) - (j x i) + to (j x j) - to (j x k) = 8 k + 4 j + k -to jeg = -to jeg + 4 j + 9 k
Nu betragter vi det skalære produkt mellem u og den vektor, der er resultatet af den foregående operation, idet vi indstiller operationen til 0:
eller (v x w) = (-3 jeg + k j + to k) · (-to jeg + 4 j + 9 k) = 6 + 4k +18 = 0
24 + 4k = 0
Den søgte værdi er: k = - 6
Så vektoren eller det er:
eller = <-3, -6, 2>
-Dyrke motion to
Figuren viser et objekt, hvis vægt er W = 600 N, der hænger i ligevægt takket være kablerne placeret i vinklerne vist i figur 3. Er det muligt at anvende Lamys sætning i denne situation? Under alle omstændigheder finde størrelsen af T1, Tto Y T3 der muliggør balance.
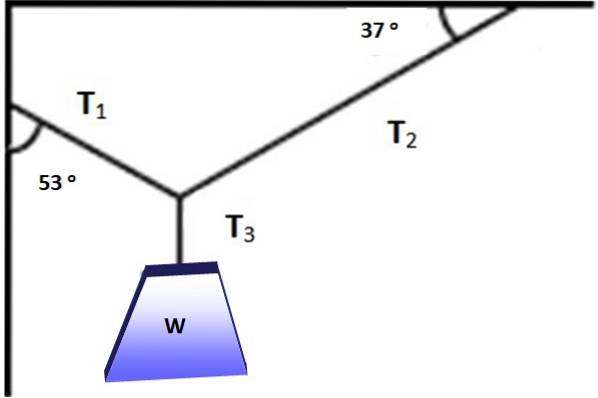
Opløsning
Lamys sætning er anvendelig i denne situation, hvis den node, som de tre spændinger påføres, overvejes, da de udgør et system af coplanar kræfter. For det første laves fritlegemsdiagrammet for hængende vægt for at bestemme størrelsen af T3:
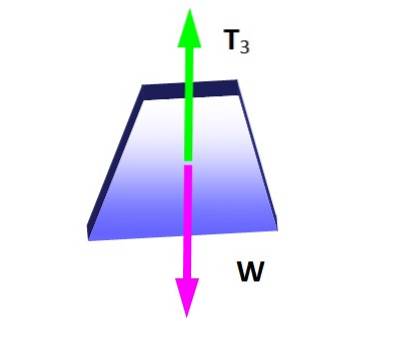
Fra ligevægtsbetingelsen følger det:
T3 = W = 600 N
Vinklerne mellem kræfterne er markeret med rødt i følgende figur, det kan let verificeres, at deres sum er 360º. Nu er det muligt at anvende Lamys sætning, da en af kræfterne og de tre vinkler mellem dem er kendt:
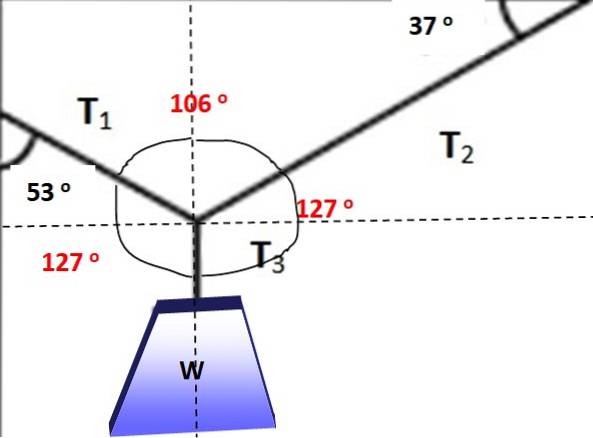
T1 / sin 127º = W / sin 106º
Derfor: T1 = sin 127º (W / sin 106º) = 498,5 N
Igen anvendes Lamys sætning til at løse Tto:
Tto / sin 127 = T1 / sin 127º
Tto = T1 = 498,5 N
Referencer
- Figueroa, D. Series: Physics for Sciences and Engineering. Bind 1. kinematik. 31-68.
- Fysisk. Modul 8: Vektorer. Gendannet fra: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mekanik for ingeniører. Statisk. 6. udgave. Continental Publishing Company 28-66.
- McLean, W. Schaum-serien. Mekanik for ingeniører: Statik og dynamik. 3. udgave. McGraw Hill. 1-15.
- Wikipedia. Vektor. Gendannet fra: es.wikipedia.org.


Endnu ingen kommentarer