
Magnetiske modstandsenheder, formler, beregning, eksempler
Det magnetisk modvilje eller magnetisk modstand er den modstand, som et medium præsenterer for passage af magnetisk flux: jo højere modvilje, jo vanskeligere er det at etablere den magnetiske flux. I et magnetisk kredsløb har modvilje den samme rolle som den elektriske modstand i et elektrisk kredsløb.
En spole kørt med en elektrisk strøm er et eksempel på et meget simpelt magnetisk kredsløb. Takket være strømmen genereres en magnetisk flux, der afhænger af det geometriske arrangement af spolen og også af intensiteten af strømmen, der strømmer gennem den..

Artikelindeks
- 1 Formler og enheder
- 2 Hvordan beregnes magnetisk reluktans?
- 3 Forskel med elektrisk modstand
- 4 eksempler
- 4.1 Solenoider
- 4.2 Spole viklet på en rektangulær jernkerne
- 5 Øvelser løst
- 5.1 - Øvelse 1
- 5.2 - Øvelse 2
- 6 Referencer
Formler og enheder
Betegner den magnetiske flux som Φm, du har:
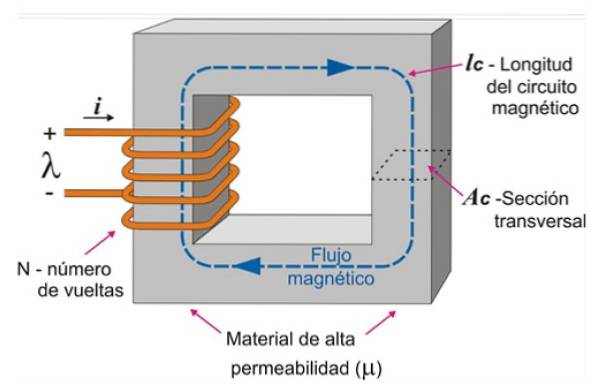
Φm = N.i / (ℓc / μAc)
Hvor:
-N er antallet af spoler.
-Strømstyrken er jeg.
-ℓc repræsenterer længden af kredsløbet.
-TILc er tværsnitsarealet.
-μ er mediets permeabilitet.
Faktoren i nævneren, der kombinerer geometrien plus mediets indflydelse, er netop kredsløbets magnetiske reluktans, en skalar størrelse, der er angivet med bogstavet ℜ, for at skelne den fra elektrisk modstand. A) Ja:
ℜ = ℓc / μ.Ac
I det internationale system for enheder (SI) måles ℜ som det inverse af henry (ganget med antallet af drejninger N). Henry er til gengæld enheden til magnetisk induktans svarende til 1 tesla (T) x kvadratmeter / ampere. Derfor:
1 TIME-1 = 1 A / T.mto
Som 1 t.mto = 1 weber (Wb), modvilje udtrykkes også i A / Wb (ampere / weber eller oftere ampere-turn / weber).
Hvordan beregnes magnetisk modvilje?
Da magnetisk reluktans har samme rolle som elektrisk modstand i et magnetisk kredsløb, er det muligt at udvide analogien med en ækvivalent med Ohms lov V = IR for disse kredsløb.
Selvom den ikke cirkulerer ordentligt, er den magnetiske flux Φm træder i stedet for strøm, mens i stedet for spænding V, definerer magnetisk spænding eller magnetkraft, analog med elektromotorisk kraft eller f. eks i elektriske kredsløb.
Magnetmotorkraften er ansvarlig for at opretholde den magnetiske flux. Forkortet f.m.m og betegnes som ℱ. Med det har vi endelig en ligning, der vedrører de tre størrelser:
ℱ = Φm . ℜ
Og sammenligner med ligningen Φm = N.i / (ℓc / μAc), det konkluderes, at:
ℱ = N.i
På denne måde kan uviljen beregnes ved at kende kredsløbets geometri og mediets permeabilitet eller også kende den magnetiske flux og den magnetiske spænding takket være denne sidste ligning, kaldet Hopkinsons lov.
Forskel med elektrisk modstand
Ligningen for magnetisk modvilje ℜ = ℓc / μAc ligner R = L / σA til elektrisk modstand. I sidstnævnte repræsenterer σ materialets ledningsevne, L er ledningens længde og A er dens tværsnitsareal.
Disse tre størrelser: σ, L og A er konstante. Imidlertid permeabiliteten af mediet μ, generelt er det ikke konstant, så den magnetiske reluktans i et kredsløb heller ikke er konstant, i modsætning til dets elektriske lignelse.
Hvis der er en ændring i mediet, for eksempel når man går fra luft til jern eller omvendt, er der en ændring i permeabilitet med den deraf følgende variation i modvilje. Og også de magnetiske materialer går igennem hysteresecyklusser.
Dette betyder, at anvendelsen af et eksternt felt får materialet til at fastholde en del af magnetismen, selv efter at feltet er fjernet..
Af denne grund er det nødvendigt, hver gang den magnetiske reluktans beregnes, nøjagtigt at specificere på hvilket punkt i cyklussen materialet er placeret og således kende dets magnetisering..
Eksempler
Selvom modvilje afhænger meget af kredsløbets geometri, afhænger det også af mediets permeabilitet. Jo højere denne værdi er, jo lavere er modviljen; sådan er tilfældet med ferromagnetiske materialer. Luft har derimod lav permeabilitet, derfor er dens magnetiske modvilje højere..
Solenoider
En solenoid er en vikling af længden ℓ lavet med N drejninger, hvorigennem en elektrisk strøm føres I. Drejningerne vikles generelt på en cirkulær måde.
Inde i det genereres et intensivt og ensartet magnetfelt, mens uden for feltet bliver omtrent nul..
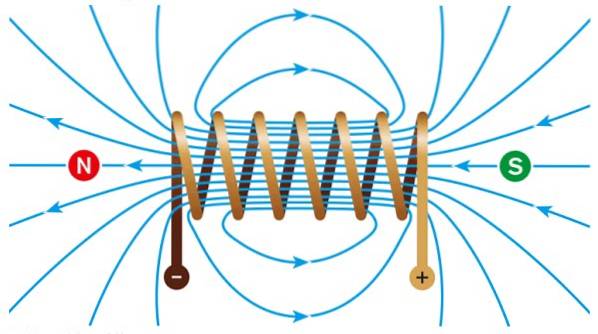
Hvis viklingen får en cirkulær form, er der en torus. Inde kan der være luft, men hvis en jernkerne placeres, er den magnetiske flux meget højere takket være den høje permeabilitet af dette mineral.
Spole viklet på en rektangulær jernkerne
Et magnetisk kredsløb kan bygges ved at vikle spolen på en rektangulær jernkerne. Når en strøm føres gennem ledningen, er det på denne måde muligt at etablere en intens feltstrøm begrænset inden i jernkernen, som vist i figur 3.
Modvilje afhænger af kredsløbets længde og tværsnitsarealet angivet i figuren. Det viste kredsløb er homogent, da kernen er lavet af et enkelt materiale, og tværsnittet forbliver ensartet..
Løst øvelser
- Øvelse 1
Find den magnetiske modvilje hos en retlinet solenoid med 2000 omdrejninger, velvidende at når en strøm på 5 A strømmer gennem den, genereres en magnetisk flux på 8 mWb.
Opløsning
Ligningen bruges ℱ = N.i at beregne den magnetiske spænding, da strømens intensitet og antallet af drejninger i spolen er tilgængelige. Det multiplicerer bare:
ℱ = 2000 x 5 A = 10.000 amp-omdrejning
Derefter bruges der ℱ = Φm . ℜ, passe på at udtrykke den magnetiske flux i weber (præfikset "m" betyder "milli", så det ganges med 10 -3:
Φm = 8 x 10 -3 Wb
Nu er modviljen ryddet, og værdierne erstattes:
ℜ = ℱ / Φm = 10.000 amp-omdrejning / 8 x 10 -3 Wb = 1,25 x 106 amp-turn / Wb
- Øvelse 2
Beregn den magnetiske reluktans for kredsløbet vist i figuren med de viste dimensioner, der er i centimeter. Kernens permeabilitet er μ = 0,005655 Tm / A og tværsnitsarealet er konstant, 25 cmto.
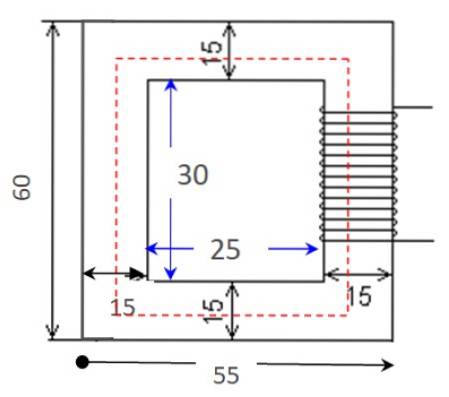
Opløsning
Vi anvender formlen:
ℜ = ℓc / μAc
Permeabilitet og tværsnitsareal er tilgængelige som data i erklæringen. Det er fortsat at finde kredsløbets længde, som er omkredsen af det røde rektangel i figuren.
Til dette beregnes længden af en vandret side i gennemsnit, idet der tilføjes større længde og kortere længde: (55 +25 cm) / 2 = 40 cm. Fortsæt derefter på samme måde for den lodrette side: (60 +30 cm) / 2 = 45 cm.
Endelig tilføjes de gennemsnitlige længder på de fire sider:
ℓc = 2 x 40 cm + 2 x 45 cm = 170 cm
Træk udskiftningsværdier i modstandsformlen, men ikke før du udtrykker tværsnitets længde og areal - givet i udsagnet - i SI-enheder:
ℜ = 170 x 10 -tom / (0,005655 Tm / A x 0,0025 mto) = 120,248 amp-drej / Wb
Referencer
- Alemán, M. Ferromagnetisk kerne. Gendannet fra: youtube.com.
- Magnetisk kredsløb og modvilje. Gendannet fra: mse.ndhu.edu.tw.
- Spinadel, E. 1982. Elektriske og magnetiske kredsløb. Nyt bibliotek.
- Wikipedia. Magnetmotorkraft. Gendannet fra: es.wikipedia.org.
- Wikipedia. Magnetisk modvilje. Gendannet fra: es.wikipedia.org.


Endnu ingen kommentarer